1363的粉丝 方法记录
1363的粉丝（1363）
题目背景
\(1363\)有一堆真正的粉丝。
\(1363\)是一奇怪的人名
题目描述
\(1363\)太帅了。
因此,他有特别多忠实粉丝，愿意献出自己寿命的\(1s\)等价交换为他的寿命\(+1s\)。
\(1363\)与粉丝们在一个\(n*n\)面积的城市中。\(1363\)可以吸收距离不超过\(s\)的粉丝所提供的寿命。
\(1363\)所在的十字路口\((a,b)\)与粉丝所在的十字路口\((c,d)\)之间距离是\(abs(a-c)+abs(b-d)\)。
\(1363\)的洪荒之力会不断变化\(q\)次，导致\(s\)的值也会变化多次。
现在要求你，最聪明的粉丝，计算出对于这\(q\)个\(s\)，每次最多增加多少秒的寿命。
输入格式
第一行三个整数\(n,k,q\)，代表城市面积为\(n*n\)，粉丝数目\(k\)，\(q\)次功力变化；
接下来\(k\)行，每行两个整数，为粉丝坐标\(x_i,y_i\);
接下来\(q\)行，每行一个整数，为当前最大距离\(s\).
输出格式
对于每次询问，输出一行。每一行只包含一个整数，代表最多增加多少秒的寿命。
样例 #1
样例输入 #1
5 5 3
1 2
5 5
3 1
1 1
5 4
2
3
4
样例输出 #1
3
3
5
提示
坐标\(x_i,y_i>0\);
对于\(30%\)的数据：\(k<=100,n<=50,q<=5\)
对于\(70%\)的数据：\(k<=10000,n<=500,q<=20\)
对于\(100%\)的数据：\(k<=500000,n<=1000,q<=20,x_i、y_i<=n,s<=10000\)
审题
根据题意，模拟一下\(1363\)的生命吮吸范围。（框中填入的值为距离\(s\)）
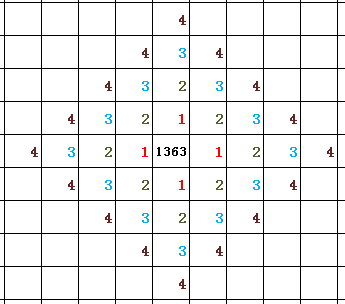
由此可见\(1363\)的生命吮吸范围是个丑陋的菱形。为了方便处理，我们需要将它变成一个正直的正方形。这里要引入两个概念。
1.曼哈顿距离
在平面上，坐标\((x_1,y_1)\)的\(i\)点与坐标\((x_2,y_2)\)的\(j\)点的曼哈顿距离为：
\(d(i,j)=abs(x_1-x_2)+abs(y_1-y_2)\)
2.切比雪夫距离
在平面上，坐标\((x_1,y_1)\)的\(i\)点与坐标\((x_2,y_2)\)的\(j\)点的切比雪夫距离为：
\(d(i,j)=max(abs(x_1-x_2),abs(y_1-y_2))\)
性质：
(1)切比雪夫距离为\(r\)的点会形成一个正方形，其边长为\(2r\)，且各边都和坐标轴平行。
(2)二维空间下，和一点的曼哈顿距离\(L1\)为定值\(r\)的点也会形成一个正方形，但其边长为\(√2r\)，而且正方形的边和坐标轴会有\(π/4(45°)\)的夹角，因此平面的切比雪夫距离可以视为平面曼哈顿距离旋转再放大后的结果。
根据这些性质，我们是不是可以通过曼哈顿距离与切比雪夫距离的转化，实现菱形到正方形的转化？
转化
题目给我们的是曼哈顿距离，我们需要将其转化为切比雪夫距离。
假设有两个点\(A(x_1,y_1),B(x_2,y_2)\)
曼哈顿距离=\(abs(x_1-x_2)+abs(y_1-y_2)\)
切比雪夫距离=\(max(abs(x_1-x_2),abs(y_1-y_2))\)
\(abs(x_1-x_2)+abs(y_1-y_2)\)
\(=max(x_1-x_2+y_1-y_2,x_1-x_2+y_2-y_1,x_2-x_1+y_1-y_2,x_2-x_1+y_2-y_1)\)
\(=max(abs((x_1+y_1)-(x_2+y_2)),abs((x_1-y_1)-(x_2-y_2)))\)
所以，当我们得到一个粉丝的坐标\((x_i,y_i)\)时，我们可以将它存到对应的切比雪夫位置\((x_i+y_i,x_i-y_i)\)。但为了防止出现负数导致无效下标，我们对纵坐标加\(n\)，并且将存粉丝位置的数组长宽各开两倍。
\(sum[i][j]\)是从\((1,1)\)到\((i,j)\)的粉丝总数。
\(p[x][1]\)和\(p[x][2]\)分别表示图上第\(x\)个点横纵坐标对应的切比雪夫值。
for(int i=1,x,y;i<=k;i++)
{
scanf("%d%d",&x,&y);
sum[x+y][x-y+n]++;
}
for(int i=1;i<=n;i++)
for(int j=1;j<=n;j++)
{
p[++pt][0]=i+j;
p[pt][1]=i-j+n;
}
统计正方形区域前缀和
\(sum[i][j]\)的定义同上。
这是一个二维前缀和维护的问题。
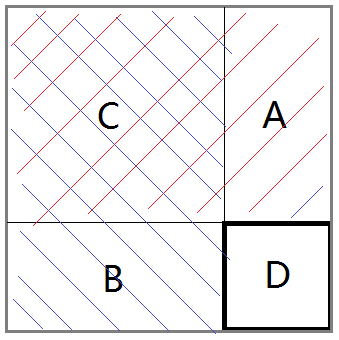
如图，若粗边框\(D\)区域为已更新区域，整个细边框区域为待更新区域。那么我们欲更新待更新区域，就可以用：
“红”+“蓝”-\(C\)+\(D\)
实现。
for(int i=1;i<=(n<<1);i++)
for(int j=1;j<=(n<<1);j++)
sum[i][j]+=sum[i-1][j]+sum[i][j-1]-sum[i-1][j-1];
有了这些预处理的加持，我们就可以暴力枚举\(1363\)坐地吸血的位置了。
AC代码
#include<iostream>
#include<algorithm>
#include<cstdio>
#include<cstring>
using namespace std;
int n,k,q,p[10000005][2],sum[2005][2005],pt,s;
int main()
{
freopen("1363.in","r",stdin);
freopen("1363.out","w",stdout);
scanf("%d%d%d",&n,&k,&q);
for(int i=1,x,y;i<=k;i++)
{
scanf("%d%d",&x,&y);
sum[x+y][x-y+n]++;
}
for(int i=1;i<=n;i++)
for(int j=1;j<=n;j++)
{
p[++pt][0]=i+j;
p[pt][1]=i-j+n;
}
for(int i=1;i<=(n<<1);i++)
for(int j=1;j<=(n<<1);j++)
sum[i][j]+=sum[i-1][j]+sum[i][j-1]-sum[i-1][j-1];
int ans=0;
while(q--)
{
scanf("%d",&s);
if(s>n+1)
{
printf("%d\n",k);
continue;
}
ans=0;
for(int i=1;i<=pt;i++)
{
int x1=max(p[i][0]-s-1,0);
int y1=max(p[i][1]-s-1,0);
int x2=min(p[i][0]+s,n<<1);
int y2=min(p[i][1]+s,n<<1);
ans=max(ans,sum[x2][y2]-sum[x2][y1]-sum[x1][y2]+sum[x1][y1]);
}
printf("%d\n",ans);
}
return 0;
}
