P1399 [NOI2013] 快餐店 方法记录
原题题面P1399
[NOI2013] 快餐店
题目描述
小 T 打算在城市 C 开设一家外送快餐店。送餐到某一个地点的时间与外卖店到该地点之间最短路径长度是成正比的,小 T 希望快餐店的地址选在离最远的顾客距离最近的地方。
快餐店的顾客分布在城市 C 的 \(N\) 个建筑中,这 \(N\) 个建筑通过恰好 \(N\) 条双向道路连接起来,不存在任何两条道路连接了相同的两个建筑。任意两个建筑之间至少存在一条由双向道路连接而成的路径。小 T 的快餐店可以开设在任一建筑中,也可以开设在任意一条道路的某个位置上(该位置与道路两端的建筑的距离不一定是整数)。
现给定城市 C 的地图(道路分布及其长度),请找出最佳的快餐店选址,输出其与最远的顾客之间的距离。
输入格式
第一行包含一个整数 \(N\),表示城市 C 中的建筑和道路数目。
接下来 \(N\) 行,每行 \(3\) 个整数,\(A_i,B_i,L_i\)(\(1\leq i\leq N\),\(L_i>0\)),表示一条道路连接了建筑 \(A_i\) 与 \(B_i\),其长度为 \(L_i\)。
输出格式
输出仅包含一个实数,四舍五入保留恰好一位小数,表示最佳快餐店选址距离最远用户的距离。
注意:你的结果必须恰好有一位小数,小数位数不正确不得分。
样例 #1
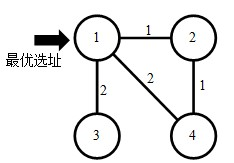
样例输入 #1
4
1 2 1
1 4 2
1 3 2
2 4 1
样例输出 #1
2.0
样例 #2
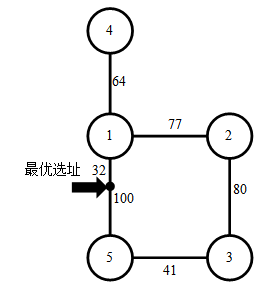
样例输入 #2
5
1 5 100
2 1 77
3 2 80
4 1 64
5 3 41
样例输出 #2
109.0
提示
样例解释 1
样例解释 2
数据范围
- 对于 \(10\%\) 的数据,\(N\leq 80\),\(L_i=1\);
- 对于 \(30\%\) 的数据,\(N\leq 600\),\(L_i\leq 100\);
- 对于 \(60\%\) 的数据,\(N\leq 2000\),\(L_i\leq 10^9\);
- 对于 \(100\%\) 的数据,\(1\leq N\leq 10^5\),\(1\leq L_i \leq 10^9\)。
审题
依照题面生成的图形是一个“含N个点,N条边的连通无向图”,符合基环树的定义。其形态为“一个环+若干子树”。
前提1:
一般树与基环树的差距就在于第N条边,有了这第N条边,才形成了一个环。若能找到环,断掉环上任意一边,那基环树就会转化成含“N个点,N-1条边”的一般树。
前提2:
若在一棵一般的树上求相同的问题,则店铺位置必定在树的直径的中点处。其与最远的顾客之间的距离即是树的直径的一半。
证明:
“现有两个顾客相距最远,则店铺必定在这条最远链上”——若店铺偏移这条链,则根据三角形斜边大于直角边,店铺距离顾客会更远;
“店铺必定在上文最远链上的中点处”——若店铺偏向某一边,则与另一边的距离会更远。
由此,我们可以推导出朴素算法。
朴素算法
思路:枚举环上每一条边,依次拆开得到不同的一般树,记录每个所得树的树的直径,取其中最短的一根作为答案链。(为什么取最短而不是最长:因为拆边是人为的选择,你可以选择断了好路走坏路,但答案就应该从好路走。注意和后面的取最大值区分)
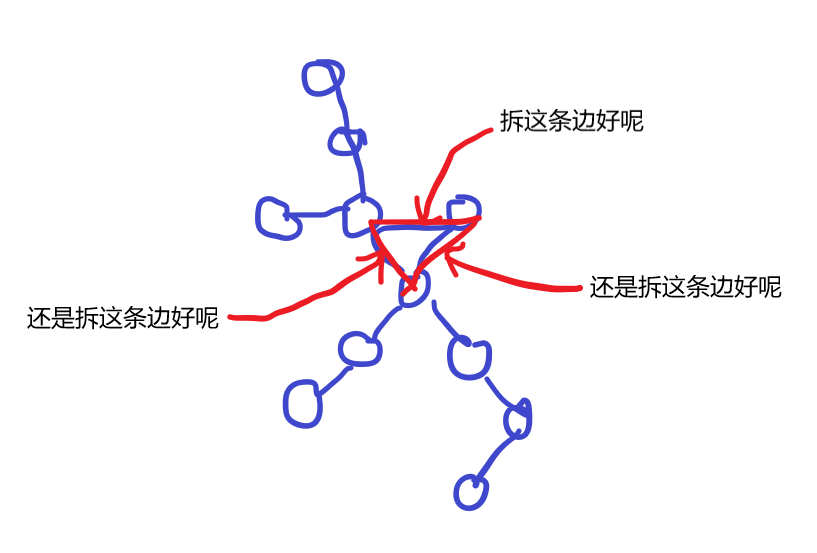
正解
case 1:答案链是环上的子树(答案链不过环)
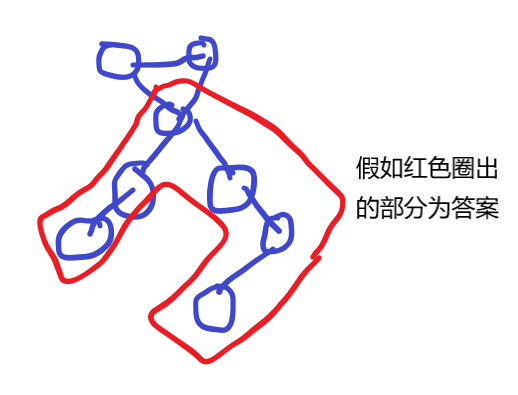
这种情况要遍历环上每一个点,求出它子树的直径并计入答案。
case 2:答案链经过环上的边(最难的情况)
如下图,我们可以讲答案链拆分成3个部分:环上点A子树的深度->环上边->环上点B子树的深度。
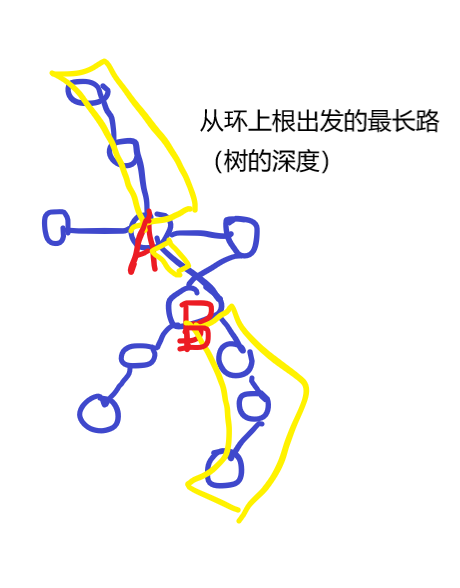
预处理环上所有点子树的树的深度dis[]
设计4个数组:\(u1\),\(v1\),\(u2\),\(v2\);
记录环上的点数为\(top\);
记录距离环上1号点的距离\(pre[]\)
记录距离环上\(top\)号点的距离\(sub[]\)
定义:
\(u1\) 前缀链长度+当前换上的节点子树最大深度\(max(dis[a]+pre[a])\)
\(v1\) 前缀中两个点子树的最大深度+两点之间的距离\(max(dis[a]+dis[b]-pre[a]+pre[b])\)
\(u2\) 后缀链长度+当前换上的节点子树最大深度\(max(dis[a]+sub[a])\)
\(v2\) 后缀中两个点子树的最大深度+两点之间的距离\(max(dis[a]+dis[b]+sub[a]-sub[b])\)
\(v1\)和\(v2\)是一条完整的链,可以直接对答案作出贡献。而\(u1\),\(u2\)通过1号点和\(top\)号点之间的连边相连接,整条链的长度为\(u1+u2+(1->cnt长度)\)
最后生成的备选答案\(ans=max(v1,v2,u1+u2+(1->cnt长度))\)
然后在备选答案中选出最小的作为最终答案。(这个过程可以加以二分优化,相当于锦上添花)
更多细节以及函数功能设计详见代码部分。
点击查看代码
#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cstring>
#define int long long
using namespace std;
const int N=100010;
int n,idx,head[N],to[N<<1],nxt[N<<1],val[N<<1];
int dis[N],ans,sum,maxans;
int u1[N],v1[N],u2[N],v2[N];
//u1 前缀链长度+当前换上的节点子树最大深度
//v1 前缀中两个点子树的最大深度+两点之间的距离
//u2 后缀链长度+当前换上的节点子树最大深度
//v2 后缀中两个点子树的最大深度+两点之间的距离
int b[N],c[N];
bool ring[N];
int maxx(int x,int y)
{
return x>y?x:y;
}
int minn(int x,int y)
{
return x>y?y:x;
}
void add(int a,int b,int c)
{
nxt[++idx]=head[a];
to[idx]=b;
val[idx]=c;
head[a]=idx;
}
int id[N],tot;
int st[N],top;
int pre[N];
void dfs(int x)//找环并记录环 tarjan
{
id[x]=++tot;//id=dfn
for(int i=head[x];i;i=nxt[i])
{
int y;
if((y=to[i])!=pre[x])
{
if(!id[y])
{
pre[y]=x;
c[y]=val[i];
dfs(y);
}
else if(id[y]>id[x])
{
while(x!=y)
{
st[++top]=y;
b[top]=c[y];
ring[y]=1;
y=pre[y];
}
st[++top]=x;
b[top]=val[i];
ring[x]=1;
return ;
}
}
}
}
void dp(int x,int fa)//dis[i]表示所在的子树的直径
{
for(int i=head[x];i;i=nxt[i])
{
if(to[i]!=fa&&!ring[to[i]])
{
dp(to[i],x);
ans=maxx(ans,dis[x]+dis[to[i]]+val[i]);
dis[x]=maxx(dis[x],dis[to[i]]+val[i]);
}
}
}
signed main()
{
scanf("%lld",&n);
for(int i=1;i<=n;i++)
{
int u,v,w;
scanf("%lld%lld%lld",&u,&v,&w);
add(u,v,w);
add(v,u,w);
}
dfs(1);
for(int i=1;i<=top;i++) dp(st[i],0);
for(int i=1;i<=top;i++)//top环上总点数
{
sum+=b[i-1];//sum作前缀
u1[i]=maxx(u1[i-1],sum+dis[st[i]]);//子树深度+前缀长度
v1[i]=maxx(v1[i-1],sum+dis[st[i]]+maxans);//用之前最深的+当前子树深度+环上经过距离
maxans=maxx(maxans,dis[st[i]]-sum);
}
int tmp=b[top];//环上子树前面的边
maxans=sum=b[top]=0;
for(int i=top;i>=1;i--)
{
sum+=b[i];//sum作后缀
u2[i]=maxx(u2[i+1],sum+dis[st[i]]);//子树深度+后缀长度
v2[i]=maxx(v2[i+1],sum+dis[st[i]]+maxans);//用之前最深的+当前子树深度+环上经过距离
maxans=maxx(maxans,dis[st[i]]-sum);
}
int minans=v1[top];
for(int i=1;i<top;i++)
{
minans=minn(minans,maxx(maxx(v1[i],v2[i+1]),tmp+u1[i]+u2[i+1]));
//max(前缀中的最大直径,后缀中的最大直径,前缀i与后缀i+1跨过1~top的所有边组成的直径)
}
ans=maxx(ans,minans);
printf("%.1lf",ans/2.0);
return 0;
}



