P1886 滑动窗口 /【模板】单调队列 方法记录
滑动窗口 /【模板】单调队列
题目描述
有一个长为 \(n\) 的序列 \(a\),以及一个大小为 \(k\) 的窗口。现在这个从左边开始向右滑动,每次滑动一个单位,求出每次滑动后窗口中的最大值和最小值。
例如:
The array is \([1,3,-1,-3,5,3,6,7]\), and \(k = 3\)。
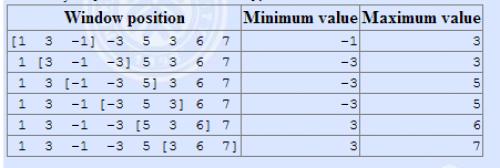
输入格式
输入一共有两行,第一行有两个正整数 \(n,k\)。
第二行 \(n\) 个整数,表示序列 \(a\)
输出格式
输出共两行,第一行为每次窗口滑动的最小值
第二行为每次窗口滑动的最大值
样例 #1
样例输入 #1
8 3
1 3 -1 -3 5 3 6 7
样例输出 #1
-1 -3 -3 -3 3 3
3 3 5 5 6 7
提示
【数据范围】
对于 \(50\%\) 的数据,\(1 \le n \le 10^5\);
对于 \(100\%\) 的数据,\(1\le k \le n \le 10^6\),\(a_i \in [-2^{31},2^{31})\)。
算法:单调队列
单调队列的性质
性质1:单调性
队列中的元素必须满足单调性。如果要求区间最大值,则队列单调递减;否则队列单调递增。即:队首就是要求的元素。
性质2:有序性
事实上,元素在原序列中的相对位置和在队列中的相对位置不变
我们可能进行的操作(“队列”指我们用到的单调序列,“原序列”指输入的序列)
以进行求窗口中最小值为例。
一.当队列中无元素时,直接将原序列中的元素从队尾入队;
二.当队列中有元素时,面对即将进入的元素,若队列中的元素大于即将进入的元素,则队列中的元素不可能成为窗口中的最小值,队列中的元素从队尾出队,新元素从队尾入队。这样以来,队列中的元素就保证是单调递增的;
三.当有新元素进入时,由于不知道之后进入的元素是否比它小,那么这个元素依然有可能成为窗口中的最小值;
四.模拟窗口滑动:如果当前遍历位置与队首位置的区间大于窗口,则重复执行队首右移;
五.生成答案:当遍历的位置第一次超过窗口大小时,每遍历一个元素就会生成一个答案。由于维护的队列单调递增,则每次队首元素就是答案。
程序上的操作参见代码注释。
点击查看代码
#include<iostream>
#include<cstdio>
using namespace std;
const int N=1000005;
int n,k,h,t;
int a[N],q1[N],q2[N];
int main()
{
scanf("%d%d",&n,&k);
for(int i=1;i<=n;i++) scanf("%d",&a[i]);
//t--队尾出,h++队首出,t++队尾进
//q1[],q2[]储存的都是位置,只有a[]储存的是值
for(int i=1;i<=n;i++)
{
while(h<=t&&i-q1[h]>=k) h++;
while(h<=t&&a[i]<a[q1[t]]) t--;
q1[++t]=i;
if(i>=k) printf("%d ",a[q1[h]]);
}
puts("");
for(int i=1;i<=n;i++)
{
while(h<=t&&i-q2[h]>=k) h++;
while(h<=t&&a[i]>a[q2[t]]) t--;
q2[++t]=i;
if(i>=k) printf("%d ",a[q2[h]]);
}
return 0;
}



