作业三:对最大子段和程序进行单元测试
题目要求
问题: 给定n个整数(可能为负数)组成的序列a[1],a[2],a[3],…,a[n],求该序列如a[i]+a[i+1]+…+a[j]的子段和的最大值。当所给的整数均为负数时定义子段和为0,依此定义,所求的最优值为: Max{0,a[i]+a[i+1]+…+a[j]},1<=i<=j<=n
例如,当(a[1],a[2],a[3],a[4],a[5],a[6])=(-2,11,-4,13,-5,-2)时,最大子段和为20。
-- 引用自《百度百科》
测试要求
1.请从语句覆盖、判定覆盖、条件覆盖、判定/条件覆盖、>条件组合覆盖五个覆盖标准中(条件组合覆盖难度较大,鼓励尝试,但请谨慎选择),任选一个标准设计测试用例
2. 请利用自动测试工具对程序进行测试
3. 请将程序运行结果和自动测试分析结果截图附到博客中
First Impression
初看到这题就觉得很熟悉....这莫不是在POJ曾经写过的是二十几道题之一.反手百度“最大子段”,看到了“动态规划”这几个关键词就确定了。确认过关键词,是我做过的题...
还记得当初想先遍历一遍找的数组中最大的一个正数,然后向前向后搜索,又想到左右全为负数的并且还有一段连续略小于最大的整数的子段的话,还是不行.....
算法分析
设从第二个元素的就为最大子段,然后动态延伸或者选择新的子段,返回最大子段和。
从第二个数遍历数组,并将每一次移动后产生的的子段和记下,并判断上一次记下的子段和是否是否为正数,如果是,则将现有子段加入上一子段中,否则,放弃上一字段,从当前子段重新动态规划。
流程图
graph TD
A[开始]-->B[i=0]
B-->L[i++]
C{b的i-1项是否大于零}
L-->C
C-->|是|D[b的i项=b的i-1项+a的第i项]
C-->|否|E[b的第i项=a的第i项]
D-->F
E-->F
F[b的第i项是否大于Max]
F-->|是|G[Max=b的第i项]
F-->|否|H
G-->|否|H{i<6}
H-->|是|I[返回Max]
H-->|否|L
单元测试
这种算法确实简单高效,但毕竟是别人的,为我们所有的时候还是先来测试测试吧,实践是检验真理的唯一标准嘛。
- 程序条件共有3条
- b[i-1]是否大于0;
- b[i]是否大于Max
- i是否小于6;
则条件组合在i取值于[1,5]时有如下情况:
| b[i]>Max | b[i]<=Max | |
|---|---|---|
| b[i-1]>0 | b[i]>Max,b[i-1]>0 | b[i-1]>0,b[i]<=Max |
| b[i-1]<=0 | b[i-1]<=0,b[i]>Max | b[i-1]<=0,b[i]<=Max |
| 即共在i循环5此情况下 |
(2 \times 2)^5=32768
种条件组合,由于组合次数过大不予考虑。
·以上是这样想是不对的
条件组合只有2x2x2=8种,上面是我以前的想法,是条件组合的组合,想太麻烦了。今天和辛娟娟同学讨论了一下条件组合覆盖,发现可以尝试一条测试案例可以尽可能的包括多个条件组合,接下来是讨论结果。
条件组合覆盖
条件分析
判定一:A.b[i-1]>0 B.b[i-1]<=0
判定二:C.b[i]>=Max D.b[i]<Max
判定三:E.i<6 F.i>=6
测试案例选取
案例1:a[6]=
| 0 | i=1 | i=2 | i=3 | i=4 | i=5 | i=6 | |
|---|---|---|---|---|---|---|---|
| a[i] | 1 | 1 | 1 | -4 | 0 | 10 | 12 |
| b[i] | 1 | 2 | 3 | -1 | -1 | 9 | 21 |
| Max | 0 | 2 | 3 | 3 | 3 | 3 | 12 |
| 条件组合 | ACE | ADE | ADE | BDE | BCE | ACF |
案例2:a[6]=
| 0 | i=1 | i=2 | i=3 | i=4 | i=5 | i=6 | |
|---|---|---|---|---|---|---|---|
| a[i] | 1 | 1 | 1 | -4 | 0 | 10 | 2 |
| b[i] | 1 | 2 | 3 | -1 | -1 | 9 | 21 |
| Max | 0 | 2 | 3 | 3 | 3 | 3 | 12 |
| 条件组合 | ACE | ADE | ADE | BDE | BCE | ADF |
案例3:a[6]=
| 0 | i=1 | i=2 | i=3 | i=4 | i=5 | i=6 | |
|---|---|---|---|---|---|---|---|
| b[i] | 1 | 2 | 3 | -1 | -1 | 9 | 21 |
| Max | 0 | 2 | 3 | 3 | 3 | 3 | 12 |
| 条件组合 | ACE | ADE | ADE | BDE | BDE | BCF |
案例4:a[6]=
| 0 | i=1 | i=2 | i=3 | i=4 | i=5 | i=6 | |
|---|---|---|---|---|---|---|---|
| b[i] | 1 | 2 | 3 | -1 | -1 | 9 | 3 |
| Max | 0 | 2 | 3 | 3 | 3 | 3 | 12 |
| 条件组合 | ACE | ADE | ADE | BDE | BDE | BDF |
即四条测试案例即可覆盖八种条件组合
接下来考虑条件判定覆盖,由于判定条件中仅一条条件,所以条件/判定覆盖等价于判定覆盖或条件覆盖。(Emmm,但这样就有分值差了啊!!!我也想实现条件判定覆盖啊!!可动态规划算法就是这样子的单条件啊~~~~)
设置测试案例为:
| b[i]>Max,b[i-1]>0 | b[i-1]>0,b[i]<=Max | b[i-1]<=0,b[i]>Max | b[i-1]<=0,b[i]<=Max |
|---|---|---|---|
| (1,2,4,8,17,50) | (1,2,3,4,5,6) | (-1,2,3,-4,5,7) | (-1,4,-2,5,-3,-9) |
测试结果
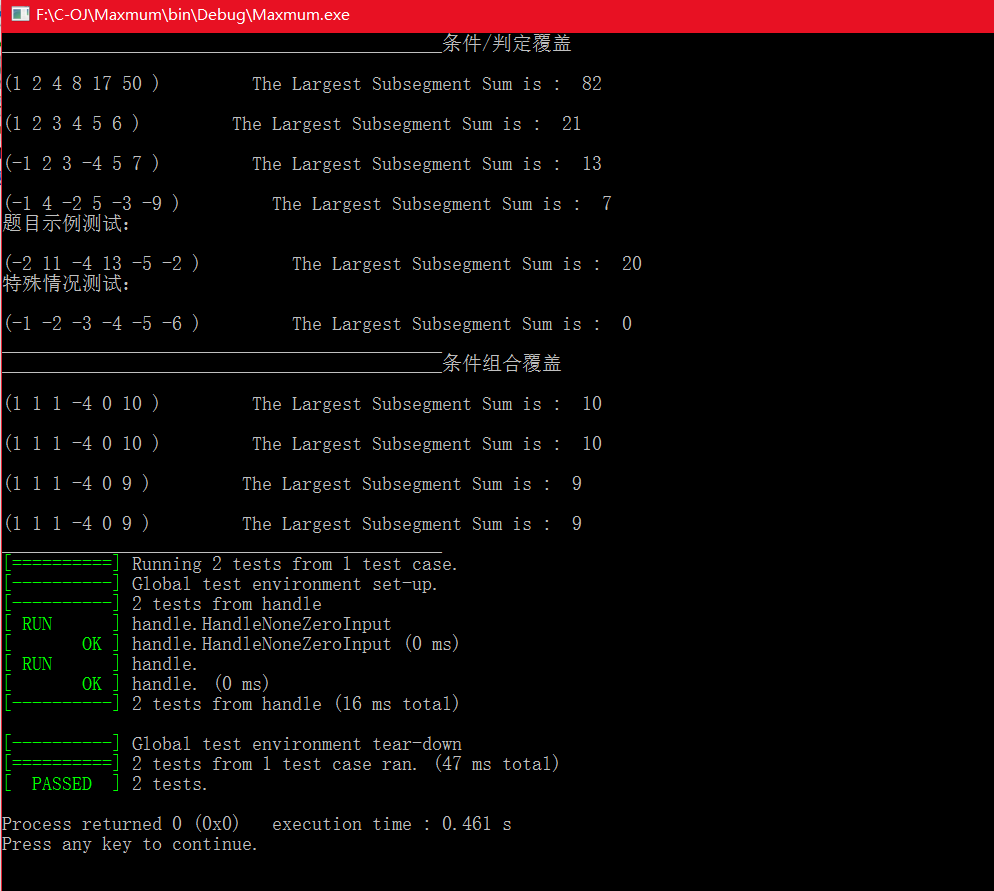
Link To Coding
https://coding.net/u/liukehong666/p/TheLargestSubsegmentSum/git/tree/master/?public=true


