Java数据结构和算法 - 什么是2-3-4树
Q1: 什么是2-3-4树?
A1: 在介绍2-3-4树之前,我们先说明二叉树和多叉树的概念。
二叉树:每个节点有一个数据项,最多有两个子节点。
多叉树:(multiway tree)允许每个节点有更多的数据项和更多的子节点。在多叉树中,节点的数据项是按关键字升序排列。
A1: 2-3-4树就是多叉树,它的每个节点最多有3个数据项和4个子节点。

2-3-4树中的2、3、4的含义是指一个节点可能包含的子节点的个数。
对非叶节点有三种可能的情况:
1) 有1个数据项的节点总是有2个子节点
2) 有2个数据项的节点总是有3个子节点
3) 有3个数据项的节点总是有4子节点
简而言之,非叶节点的子节点数总是比它含有的数据项多1。
L = D + 1
设L是子节点链接的个数,D是数据项的个数。
比较来说,叶节点没有子节点,然而它可能还有1个、2个或3个数据项。空节点是不会存在的。
所有的叶节点都在同一层上。
Q2: 为什么不称2-3-4树为1-2-3-4树呢? 它的节点不能像二叉树那样只有一个节点吗?
A2: 二叉树中,节点最多有两个子节点的链接。它当然可以只有一个链接,指向它的左子节点或右子节点。它的另一个链接可以是一个NULL值。
然而,在2-3-4树中,不允许只有一个链接,有一个数据项的非叶节点必须总是保持有两个链接,除非它是叶节点,但是在那种情况下会没有链接。
Q3: 如何组织2-3-4树?
A3: 为了方便起见,用从0到2的数字给数据项编号,用0到3给子节点编号。如下图:
有两个链接的节点称为2-节点,有三个链接的称为3-节点,有四个链接的称为4-节点,但没有称为1-节点的节点。
节点中的数据项是按关键字升序排列,习惯上从左到右升序。

A3: 2-3-4树的规则:
1) 根是child0的子树的所有子节点的关键字K < key0
2) 根是child1的子树的所有子节点的关键字key0 < K < key1
3) 根是child2的子树的所有子节点的关键字key1 < K < key2
4) 根是child3的子树的所有子节点的关键字K > key2
2-3-4树一般不允许出现重复关键字值
Q4: 如何实现2-3-4树的Java代码?
A4: 完整代码见https://gitee.com/firewaycoding/ds_in_java/blob/master/chapter10/01Tree234/src/Tree234.java
Q5: 单元测试用例应该覆盖哪些场景?
A5: 插入和查找。
Q6: 插入操作?
A6: 以插入[194, 210, 130, 142, 226, 34, 74, 178, 46, 38, 170, 98, 218, 278, 70, 118, 146, 174, 114, 106, 50, 158, 282, 138, 90, 266, 274, 78, 86, 94, 214, 242]为示例。

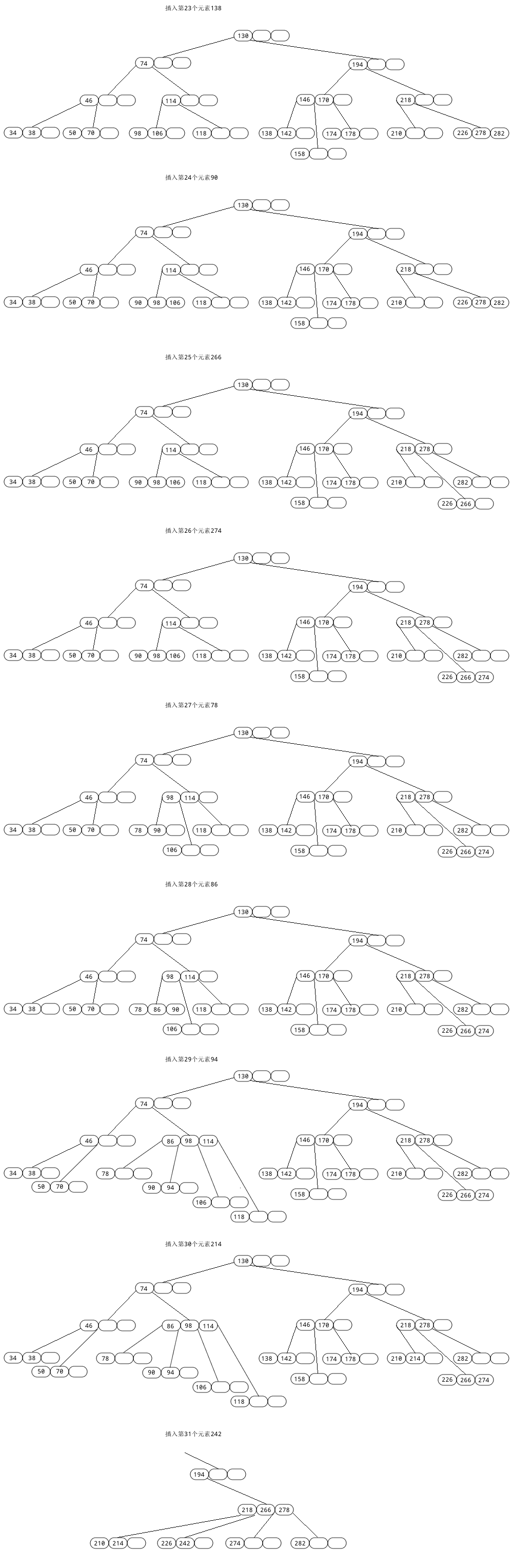
从上面我们可以总结出以下几点:
1) 新的数据项总是插在叶节点里,在树的最底层;
2) 查找时没有碰到满节点,插入很简单,找到合适的叶节点后,只要把新数据项插入进去就可以;
3) 如果往下寻找要插入的路途中,遇到满节点,需要节点先分裂,正如上图插入第17个元素,第21个元素,好好体味节点分裂和根节点分裂的细微差异;
4) 注意节点分裂是把数据向上和向右移动,正是这样的重新排列才保持了树的平衡
Q7: 怎样把2-3-4树转化为红黑树?
A7: 有3条规则:
1) 把2-3-4树中的每个2-节点转化为红黑树的黑节点; 
2) 把每个3-节点转化为一个子节点和父节点,哪个节点变成子节点或父节点都无所谓。子节点涂成红色,父节点涂成黑色;

3) 把每个4-节点转化为一个父节点和两个子节点。子节点涂成红色,父节点涂成黑色;
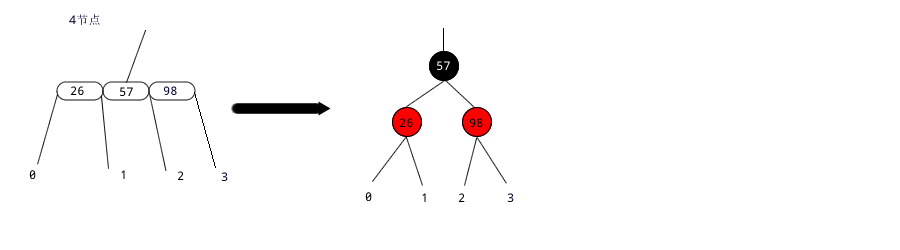
下面展示了一棵2-3-4树和应用这些规则转化后的红黑树。

Q8: 如何证明2-3-4树的分裂与红黑树的颜色变换、旋转的等价性?
A8: 2-3-4树中用节点分裂保持平衡,红-黑树中用颜色变换和旋转保持平衡。
1) 4-节点分裂和颜色变换

2) 3-节点分裂和旋转
有两种可能的排列方式。主要是以3-节点的两个数据项中的哪个作为父节点。

注意,左倾旋转得来的树和右倾的树是一样的。因此红-黑树的旋转和把2-3-4树转换为红-黑树时选择哪个节点做父节点是等价的。
Q8: 2-3-4树的效率
A: 在时间方面,树的搜索时间与树的层数成正比,特别的是,2-3-4树中的每个节点最多可以有4个子节点,如果每个节点都是满的,树的高度应该和Log4N成正比。不过它们不可能是满的,因此,2-3-4树的的高度大致在(Log2(N + 1)) / 2和Log2(N + 1)之间。
另一方面,因为节点用线性搜索来查看数据项,也消耗一点时间,有些节点有一个数据项,有些有两个,有些有三个,如果按平均两个来计算,查找的时间和2 * Log4成正比。在大O表示法中这个小的常数可以忽略。
因此,2-3-4树中的查找时间与平衡二叉树如红-黑树大致相等,都是O(logN)。
A: 在空间方面,2-3-4树每个节点保存三个数据项的引用和四个子节点的引用,这些空间可以用数组的方式来分配。可能会想到用链表来代替数组,但对只有三个或四个数据项来说,链表的额外开销和数组比起来,用链表也许不是一个很好的方法。
不过,使用数组的方式,大约有2/7的可用空间浪费了。怎么说呢? 比如只有一个数据项的节点会浪费2/3的数据项存储空间和1/2的子节点存储空间,两个数据项的节点会浪费1/3的数据项存储空间和1/4的子节点存储空间,如果按每个节点有两个数据项来计算,大约就有2/7的存储空间浪费。
参考资料
- 《Java数据结构和算法》第2版第10章2-3-4树



 浙公网安备 33010602011771号
浙公网安备 33010602011771号