数据库内核:PostgreSQL Join
Join 实现
Join 简介
数据库管理系统是一个用以存储,结合(Combine)和过滤(Filter)信息的引擎。Join(\(\bowtie\))就是最主要的结合信息的方法。Join 操作非常重要,但是成本也可能非常高。最普遍的 Join 就是等价 Join,例如 \(R.pk=S.fk\)。所有 Join 操作的变体(比如 inner,outer,semi,anti,natural 等)都基本一致,实现 Join 操作有 3 种方式:
- nested loop:简单、应用广泛、由于没有使用缓冲区,所以效率不高
- sort-merge:如果 Join 的属性在表中是排序了的,那么效率是最高的
- hash-based:需要一个好的哈希函数和充足的缓冲区
Join 例子
现在有一个 university 数据库,它有以下几张表:
create table Student(
id integer primary key,
name text,
...
);
create table Enrolled(
stude integer references Student(id),
subj text references Subject(code),
...
);
create table Subject(
code text primary key,
title text,
...
);
目标是“列出所有学科 Subject 的学生姓名,按学科 Subject 排列”,其相对应的 SQL 如下:
select E.subj, S.name
from Student S, Enrolled E
where S.id = E.stude
order by E.subj, S.name;
其相应的关系代数表示是 \(Sort_{[subj]}(Project_{[subj,name]}(Join_{[id=stude]}(Student,Enrolled)))\)
为了方便后面的成本分析,\(N\) 表示内存缓冲区的数量,还有一些数据库统计:
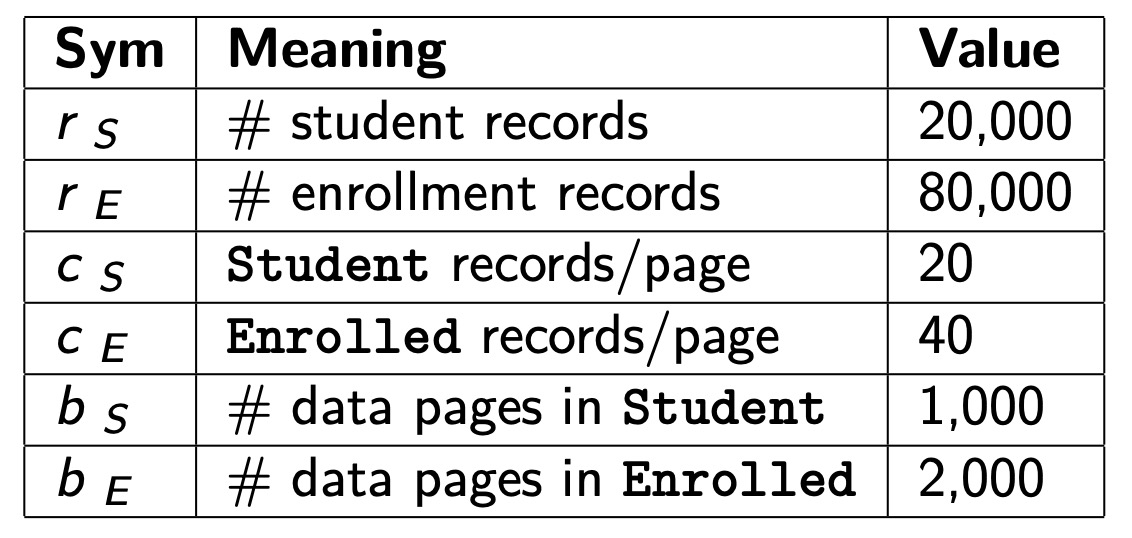
\(out=Student\bowtie Enrolled\) 的统计信息如下:

- \(r_{out}\):之所以最后的元组数量为 80,000,是因为在 Enrollment 表中的所有元组都会与 Student 表中的元组有所对应。
- \(C_{out}\):因为最后的结果元组中,只会有
subject和name两个属性,所以每一页中可容纳的元组数量就增加了。
最朴素的 Join 方法就如下所示:
for each tuple TS in Students {
for each tuple TE in Enrolled {
if (testJoinCondition(C,TS ,TE )) {
T1 = concat(TS ,TE )
T2 = project([subj,name],T1)
ResultSet = ResultSet ∪ {T2}
} } }
循环遍历两个关系中的所有元组,只要满足 Join 条件就进行拼接,从拼接的结果中提取需要的属性,存入结果集。在这个过程中:
- 一共进行了 \(r_S*r_E=20000*80000=16*10^8\) 次
testJoinCondition() - 一共扫描了 \(r_S+r_S*r_E=20000+20000*80000\) 个元组
当然我们也可以选择将对 Enrolled 关系的遍历放在外循环,但这个时候,扫描的元组数量就更多了。
Nested Loop Join
基本策略(\(R.a\bowtie S.b\))
Result = {}
for each page i in R {
pageR = getPage(R,i)
for each page j in S {
pageS = getPage(S,j)
for each pair of tuples tR ,tS from pageR,pageS {
if (tR .a == tS .b)
`Result = Result ∪ (tR :tS )
} } }
需要 R 和 S 的输入缓冲区和 “joined” 元组的输出缓冲区。上面代码中,我们认为 R 是外关系,S 是内关系。其成本为 \(Cost=b_R*b_S\)。
Block Nested Loop Join
当内存中有 \(N\) 个缓冲区时,就可以使用一个缓冲区来读取关系 S(内关系),一个缓冲区作为输出缓冲区来存储结果,剩下的 \(N-2\) 个缓冲区用来读取关系 R (外关系)的页面 Chunk。
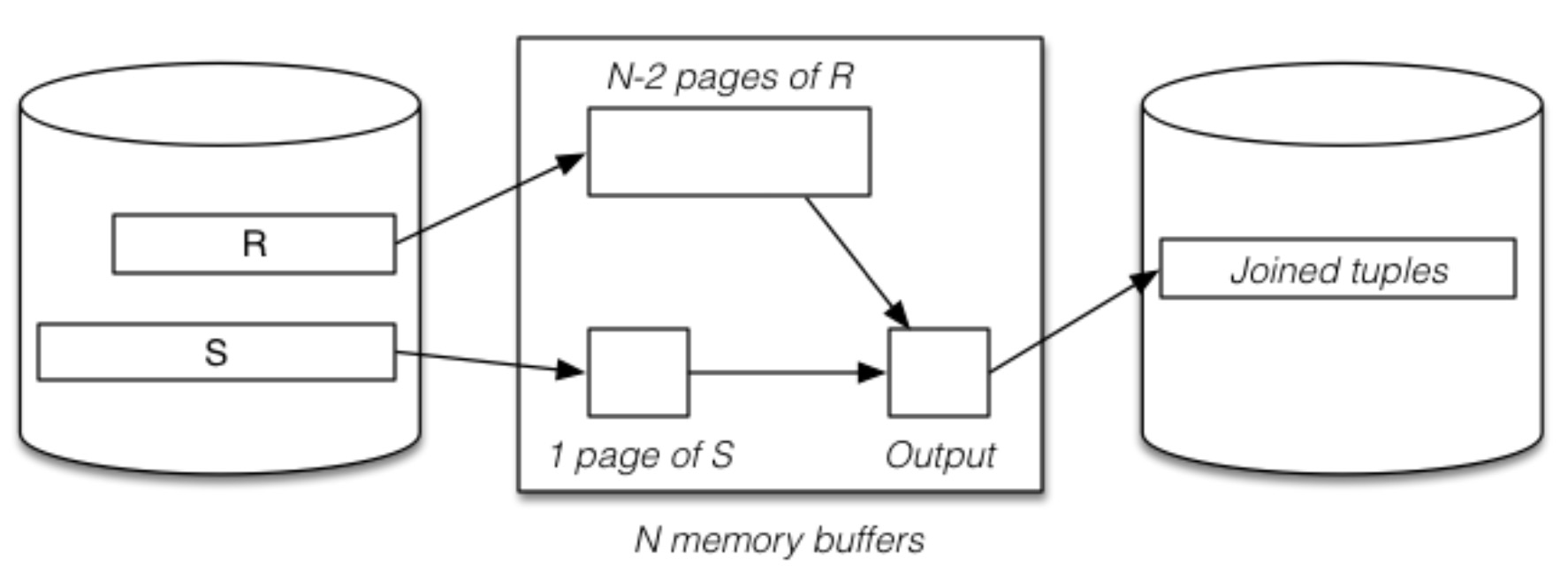
对每个关系 S 的页面,检查缓冲区所有 \((t_R,t_S)\) 对的 Join 条件。
成本分析:
- 最好的情况:当 \(b_R\leq N-2\) 时,可以将关系 R 的所有页面都读入到缓冲区中,此时 Join 的成本为 \(Cost=b_R+b_S\)。
- 一般的情况:当 \(b_R>N-2\) 时,此时需要读 \(\lceil\frac{b_R}{N-2}\rceil\) 个页面 Chunk,对于每一个 Chunk,都需要从关系 S 中读取 \(b_S\) 个页面,因此 Join 的成本为 \(Cost=b_R+b_S*\lceil\frac{b_R}{N-2}\rceil\)
不管哪种情况,都需要进行 \(r_R*r_S\) 次元组检查。
Block Nested Loop Join 在实际中更加实用是因为很多查询如下:
select * from R,S where r.i=s.j and r.x=K;
这类查询等价于:
Tmp = Sel[x=K](R)
Res = Join[i=j](Tmp, S)
如果 Tmp 非常小,那么就能全部放入内存中,所以 Block Nested Loop Join 会更加实用。
练习 1

对于 \(N=22,202,2002\) 以及不同内外表的情况下的成本(页面获取数量)分别是多少?
- 当 \(N=22\) 时:
- 关系 S 作为内关系,关系 E 作为外关系时:此时 \(b_E>N-2\),因此其成本为 \(Cost=b_E+b_S*\lceil\frac{b_E}{N-2}\rceil=2000+1000*\lceil\frac{2000}{20}\rceil=102000\)
- 关系 E 作为内关系,关系 S 作为外关系时:此时 \(b_S>N-2\),因此其成本为 \(Cost=b_S+b_E*\lceil\frac{b_S}{N-2}\rceil=1000+2000*\lceil\frac{1000}{20}\rceil=101000\)
- 当 \(N=202\) 时:
- 关系 S 作为内关系,关系 E 作为外关系时:此时 \(b_E>N-2\),因此其成本为 \(Cost=b_E+b_S*\lceil\frac{b_E}{N-2}\rceil=2000+1000*\lceil\frac{2000}{200}\rceil=12000\)
- 关系 E 作为内关系,关系 S 作为外关系时:此时 \(b_S>N-2\),因此其成本为 \(Cost=b_S+b_E*\lceil\frac{b_S}{N-2}\rceil=1000+2000*\lceil\frac{1000}{200}\rceil=11000\)
- 当 \(N=2002\) 时:
- 关系 S 作为内关系,关系 E 作为外关系时:此时 \(b_E\leq N-2\),因此其成本为 \(Cost=b_R+b_S=1000+2000=3000\)
- 关系 E 作为内关系,关系 S 作为外关系时:此时 \(b_S\leq N-2\),因此其成本为 \(Cost=b_R+b_S=1000+2000=3000\)
练习 2
如果练习 1 示例中的查询是:
select j.code, j.title, s.name
from Student s
join Enrolled e on (s.id=e.student)
join Subject j on (e.subj=j.code);
- 之前的分析需要进行哪些改变?
- 有哪些 Join 组合?
- 假设有 2000 subjects 元组,\(c_J=10\),中间元组有多大?
- 计算 \(N = 202\) 的成本(页面获取与写入的数量)
由于是三个表进行 Join,因此需要先对其中两个进行 Join,然后产生的中间结果写入到临时的磁盘页面中,再接着将中间结果与剩下那个表进行 Join。因此,成本还需要加入将中间结果写出的成本,其余成本与上面差不多。
按照连接的先后顺序,有 \(3*2*1=6\) 种 Join 组合。例如 \(S\bowtie E\bowtie J,S\bowtie J\bowtie E...\)等等。
由于缺少信息,后两问无法做。
Index Nested Loop Join
Block Nested Loop 也是存在问题的,那就是需要反复读取内关系中的页面。如果内关系有一个索引,那么就可以很好地解决重复读的问题。以下是 \(Join_{[i=j]}(R,S)\) 的伪代码:
for each tuple r in relation R {
use index to select tuples from S where s.j = r.i
for each selected tuple s from S {
add (r,s) to result
}}
成本分析:
- 对于关系 R 进行一个扫描,仅需要一个缓冲区,因为每次只需要使用一个元组
- 对于关系 R 中的每个 元组,使用索引在关系 S 中寻找一个匹配的元组,成本取决于索引的结构以及结果的数量
其成本为 \(Cost=b_R+r_R*Sel_S\),这里的 \(Sel_S\) 就是在关系 S 中进行选择的代价,如果关系 S 使用哈希来索引,那么代价为 1。
练习 3
现在执行 \(Join_{[i=j]}(S,T)\),参数如下:
- \(r_S=1000,b_S=50,r_T=3000,b_T=600\)
- \(S.i\) 是主键,关系 T 中有 \(T.j\) 的索引
- 关系 T 按 \(T.j\) 排序,关系 S 的每一个元组都有两个 T 的元组符合 Join
- 数据库管理系统有 \(N=12\) 个缓冲区
计算分别使用 block nested loop join 和 index nested loop join 两种方法的成本,\(Cost_r\) 表示读取的页面数量,\(Cost_j\) 表示 Join 条件检查的成本。
- block nested loop join:其成本为 \(Cost_r=b_S+b_T*\lceil\frac{b_S}{N-2}\rceil=50+600*\lceil\frac{50}{12-2}\rceil=6050\),\(Cost_j=r_S*r_T=1000*3000=3000000\)
- index nested loop join:其成本为 \(Cost_r=b_S=50\),\(Cost_j=r_S*Sel_T=1000*2=2000\)。
Sort-Merge Join
Sort-Merge Join 简介
它的基本方法为:
- 基于 Join 属性给两个关系进行排序
- 同时扫描两个关系,使用 Merge 去组成结果元组
优点:
- 不需要对每个关系 R 的元组处理整个关系 S(关系 S 为内关系,关系 R 为外关系)
- 只需要处理关系 R 和关系 S 匹配的元组数量的轮次
缺点:
- 为两个关系进行排序的成本高
- 如果 Join 属性的取值有重复 (non-key attribute),此时需要 Rescanning
标准 Merge 需要两个光标,其伪代码如下:
while (r != eof && s != eof) {
if (r.val ≤ s.val) { output(r.val); next(r); }
else { output(s.val); next(s); }
}
while (r != eof) { output(r.val); next(r); }
while (s != eof) { output(s.val); next(s); }
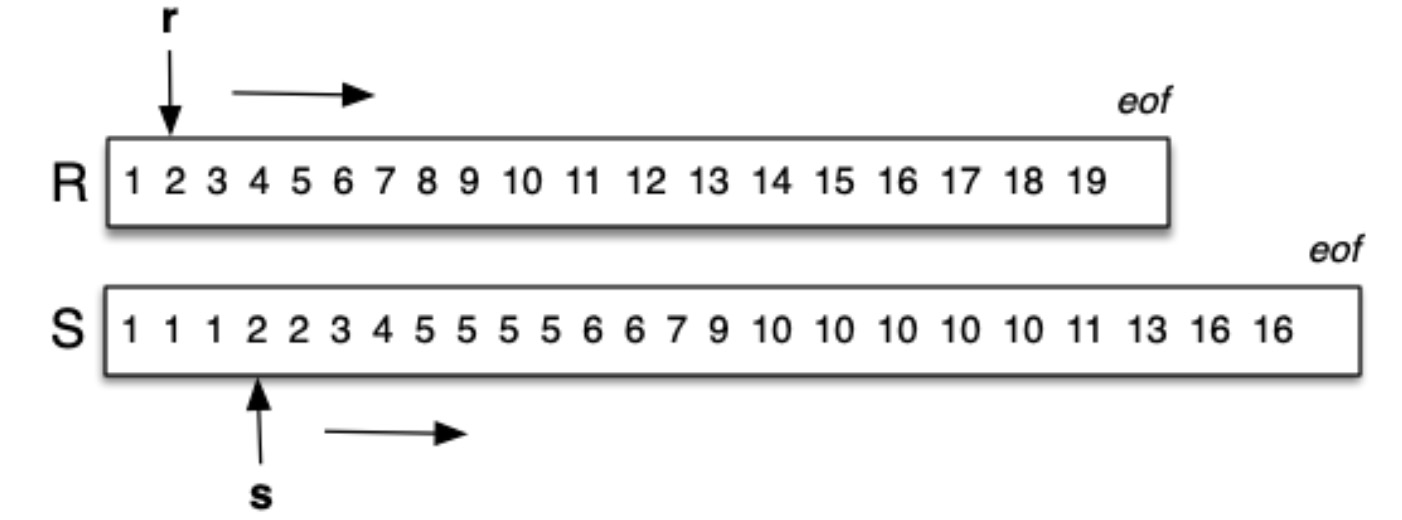
而在这里,对于 Join 的 Merge 需要 3 个光标:
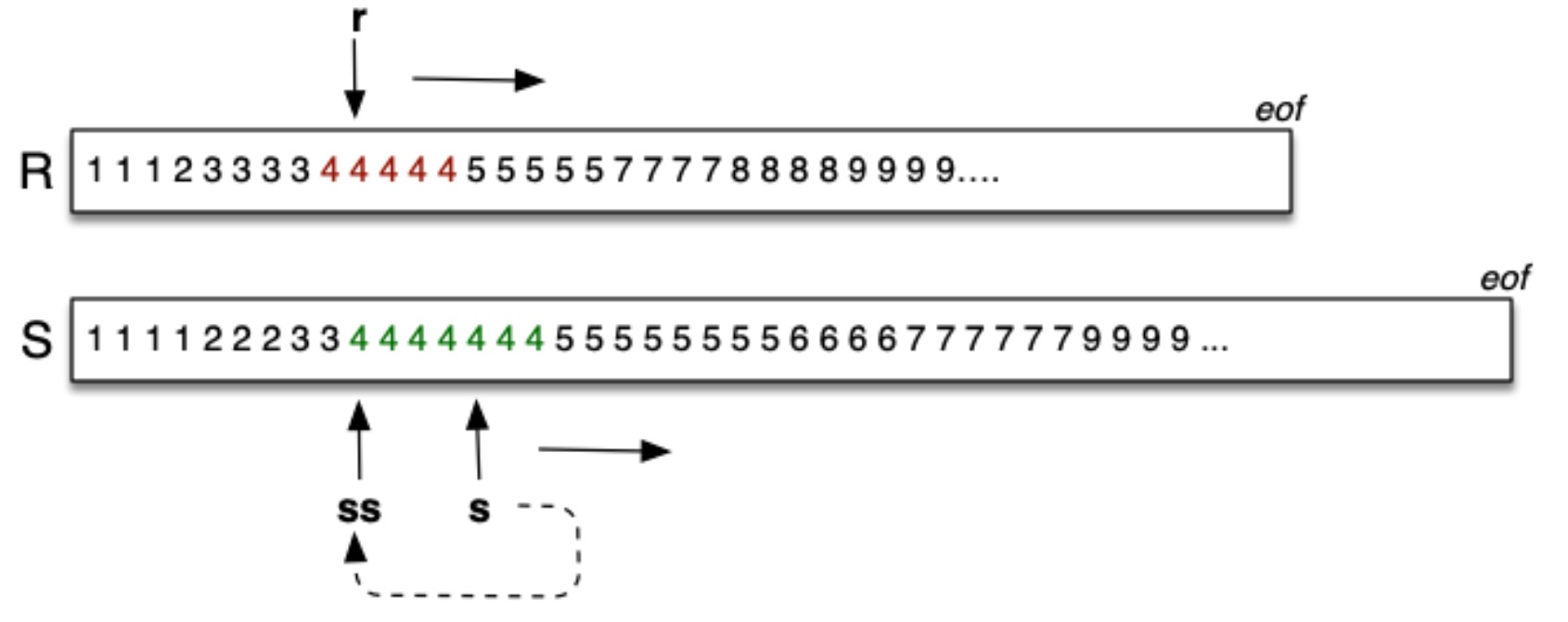
- r:关系 R 中当前的元组
- s:关系 S 中当前的元组
- ss:关系 S 中当前 一轮的起始位置
之所以需要第三个光标是因为 Join 的属性可能不是 Key 属性。比如在上图中,关系 R 和关系 S 中都有一系列 Join 属性为 4 的元组,这些元组都需要 Join。因此,在关系 R 中,我们先读到第一个 4,此时需要将其与关系 S 中的所有 4 进行 Join,然后关系 R 中下一个值仍为 4,此时就需要在 S 中重新读取这轮的 4。其伪代码如下:
Query ri, si; Tuple r,s;
ri = startScan("SortedR");
si = startScan("SortedS");
while ((r = nextTuple(ri)) != NULL && (s = nextTuple(si)) != NULL) {
while (r != NULL && r.i < s.j) // 当关系R每读完,且关系R当前元组小于关系S当前元组
r = nextTuple(ri); // 读关系R的下一个元组
if (r == NULL) break; // 关系R遍历完了
while (s != NULL && r.i > s.j)
s = nextTuple(si);
if (s == NULL) break;
TupleID startRun = scanCurrent(si) // 记下关系S当前的元组为ss
while (r != NULL && r.i == s.j) {
while (s != NULL and s.j == r.i) {
addTuple(outbuf, combine(r,s)); // 符合Join
if (isFull(outbuf)) {
writePage(outf, outp++, outbuf);
clearBuf(outbuf);
}
s = nextTuple(si);
}
r = nextTuple(ri);
setScan(si, startRun);
}
}
缓冲区的需求:
- 对于排序阶段:缓冲区越多越好,因为排序的代价为 \(O(logN)\),这里的 \(N\) 就是缓冲区的数量。如果缓冲区不够,那么排序所用的开销会十分巨大,基本占据了整个过程的主导地位。
- 对于合并阶段:一个输出缓冲区用来存储结果,一个输入缓冲区读取 关系 R,一个足够放下关系 S 中最大 Run 的输入缓冲区。
成本分析:
- 对于排序阶段:\(Cost=2b_R(1+log_{N-1}\frac{b_R}{N})+2b_S(1+log_{N-1}\frac{b_S}{N})\),这里的 \(N\) 就是缓冲区的数量。
- 对于合并阶段:如果关系 S 中的每个 Run 都能够存入缓冲区中,那么 \(Cost = b_R + b_S\)。如果关系 S 中有一些 Run 长度大于缓冲区,需要根据关系 R 中的值重复扫描 Run。
例子与练习
考虑一个如下的 SQL 查询:
select E.subj, S.name
from Student S join Enrolled E on (S.id = E.stude)
order by E.subj;
数据库管理系统的参数:\(r_S=20000,c_S=20,b_S=1000,r_E=80000,c_E=40,b_E=2000\)
例子 1:\(Join_{id=stude}(Student,Enrolled)\),两个关系都没有基于 id 排序,\(N = 32\),所有 Run 的长度都小于 30。
例子 1:\(Join_{id=stude}(Student,Enrolled)\),两个关系都已经基于 id 排序,\(N = 4\),一个作为关系 S 的输入缓冲区,两个作为关系 E 的输入缓冲区,一个作为输出缓冲区。关系 E 中 5% 的 Run 会占两个页面,在关系 S 中没有 Run,因此 id 是 S 的主键。
在上述条件下,不需要任何 rescaning。因此,其成本为 \(Cost=b_S+b_E=3000\)
Hash Join
Hash Join 简介
基本想法:使用哈希对关系进行分区,从而避免考虑所有的元组对。因此,这需要充足的内存缓冲区来容纳大部分的分区,如果能把外关系的最大分区放入其中,这将是最好的。但是该方法也存在问题,那就是只能对等式 Join 使用,而之前两种 Join 方法应用的范围更广泛。而且哈希容易出现数据偏斜。Hash Join 主要有以下 3 种变式:
- Simple Hash Join
- Grace Hash Join
- Hybrid Hash Join
Simple Hash Join
一个页面一个页面地读取外关系 R,并对当前页面中的元组进行哈希,将哈希后的元组存入内存缓冲区,这些缓冲区也称为哈希缓冲区(所有哈希缓冲区可以看作是一个哈希表,那么每一个哈希缓冲区就是一个哈希桶)。一旦有一个哈希缓冲区满了,就开始扫描内关系 S。扫描内关系 S 时,使用相同的哈希函数。如果 \(R.i = S.j\),那么 \(h(R.i) = h(S.j)\)。即会被哈希到同一个缓冲区。因此,对每一个关系 S 中的元组,只需要检查一个哈希缓冲区就可以了。
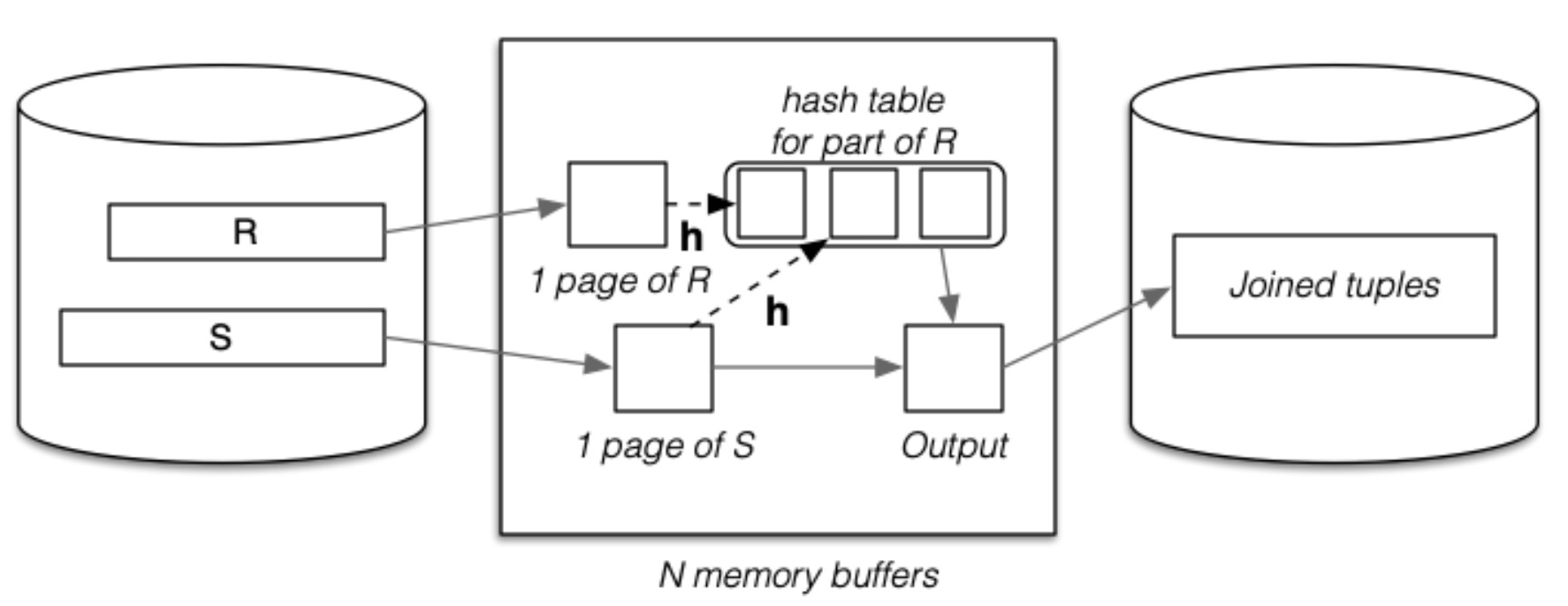
- 一个输出缓冲区
- 一个关系 R 的输入缓冲区
- 一个 关系 S 的输入缓冲区
- 剩余所有缓冲区当作哈希缓冲区
其伪代码如下:
for each tuple r in relation R {
if (buffer[h(R.i)] is full) {
for each tuple s in relation S {
for each tuple rr in buffer[h(S.j)] {
if ((rr,s) satisfies join condition) {
add (rr,s) to result
} } }
clear all hash table buffers
}
insert r into buffer[h(R.i)]
}
Simple Hash Join 在页面的读取数量上面和 Nested Loop 基本相同,但是进行 Join 检查的次数要少于 Nested Loop。
Simple Hash Join 中 Join 检查的次数小于等于 \(r_S * c_R\)(即关系 S 中元组的总数乘以一个哈希缓冲区的元组总数)。Nested Loop 中 Join 检查的次数为 \(r_S * r_R\)。
成本分析:
- 最好的情况:关系 R 的所有元组都可以放到哈希表中,此时两个关系的页面都只需要读一遍,\(Cost = b_R + b_S\)。
- 比较好的情况:再填充哈希表 m 次。 对于外关系 R,我们是分为几个 chunks 来读取,当读取某个 chunk,使得有一个哈希缓冲区被填满了,就开始读取内关系 S,当操作完关系 S 中的元组之后,就会把所有哈希缓冲区清空,继续从关系 R 中读入,重新填充这些哈希缓冲区。所以,这里的 \(m \geq \lceil\frac{b_R}{N-3}\rceil\)。此时 \(Cost = b_S + m * b_R\)。此时虽然读取页面的数量比 Nested Loop 多,但是 Join 检查的次数仍然更少。
- 最糟糕的情况:所有的元组都被哈希到同一个页面。 此时 \(Cost = b_S + b_R * b_S\)。
练习:Simple Hash Join 的成本
现在执行 \(Join_{[i=j]}(R,S)\),一些参数如下:
- \(r_R=1000,b_R=50,r_S=3000,b_S=150,c_{Res}=30\)
- \(R.i\) 是主键,关系 R 的每一个元组都有 2 个匹配的 S 元组
- 数据库管理系统有 \(N=43\) 个缓冲区
- 数据和哈希都符合均匀分布
使用 simple hash join,假设哈希表中每个分区的装填因子为 0.75。计算页面读写次数和 Join 检查次数。
一共 43 个缓冲区,去掉输入输出的 3 个缓冲区后,还剩余 40 个,由于装填因子为 0.75,所以 40 个缓冲区可以装 \(40*0.75=30\) 个页面。由于关系 R 的页面为 50 个,所以一个关系 S 的元组需要 \(m=\lceil\frac{50}{30}\rceil=2\) 次。因此,页面读的次数 \(Cost = b_S + m * b_R=150+2*50=250\)。匹配的元组数量是 \(r_R*2=2000\) 个,而结果元组每页放 \(c_{Res}=30\) 个,所以需要 \(\lceil\frac{2000}{30}\rceil=67\) 个页面。由于每个分区的装填因子为 0.75,所以每个哈希缓冲区的元组数量有 \(\frac{r_R}{b_R}*0.75=150\) 个。因此 Join 检查次数为 \(r_S * c_R=3000*(150*2)=900000\) 次。
Grace Hash Join
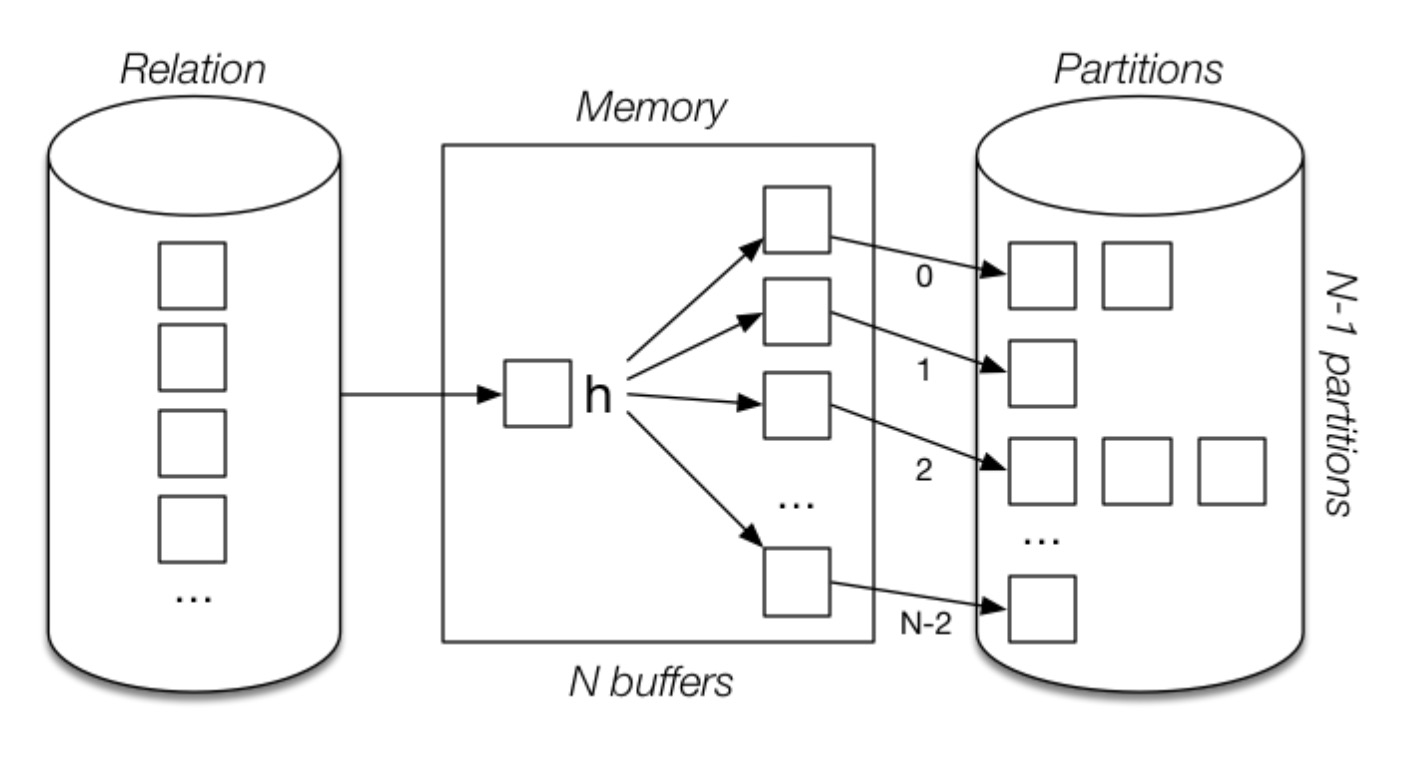
基本思路:
- 使用哈希函数 \(h1\) 基于 Join 属性对两个关系进行分区
- 对关系 R 的分区使用另一个哈希函数 \(h2\) 将其一个一个载入 \((N-3)\) 个哈希缓冲区中
- 扫描对应的关系 S 的分区去组成结果
- 重复操作直到所有分区都被扫描过
分区阶段:左侧就是关系,一个页面一个页面进行读取,对当前页面中的元组使用哈希函数将其分配到合适地输出缓冲区中,当缓冲区满了之后,写入到磁盘中对应的分区文件中。
Join 阶段:在分区阶段,由于对两个关系都是使用相同的哈希函数,所以两者的分区文件是相互对应的。而每个分区的大小也能直接装入到内存缓冲区中。此时,读入一个关系 R 的分区,并使用一个新的哈希函数 \(h2\) 来将其中的元组再分配。接下里,读入关系 S 一个对应的分区,同样对其中的元组使用 \(h2\),这就可以知道每个元组对应哪一个哈希缓冲区了,最后就在这个对应的哈希缓冲区中,寻找符合 Join 条件的元组,组成结果元组放入到输出缓冲区中。当输出缓冲区满了之后,写入磁盘并清空哈希缓冲区。
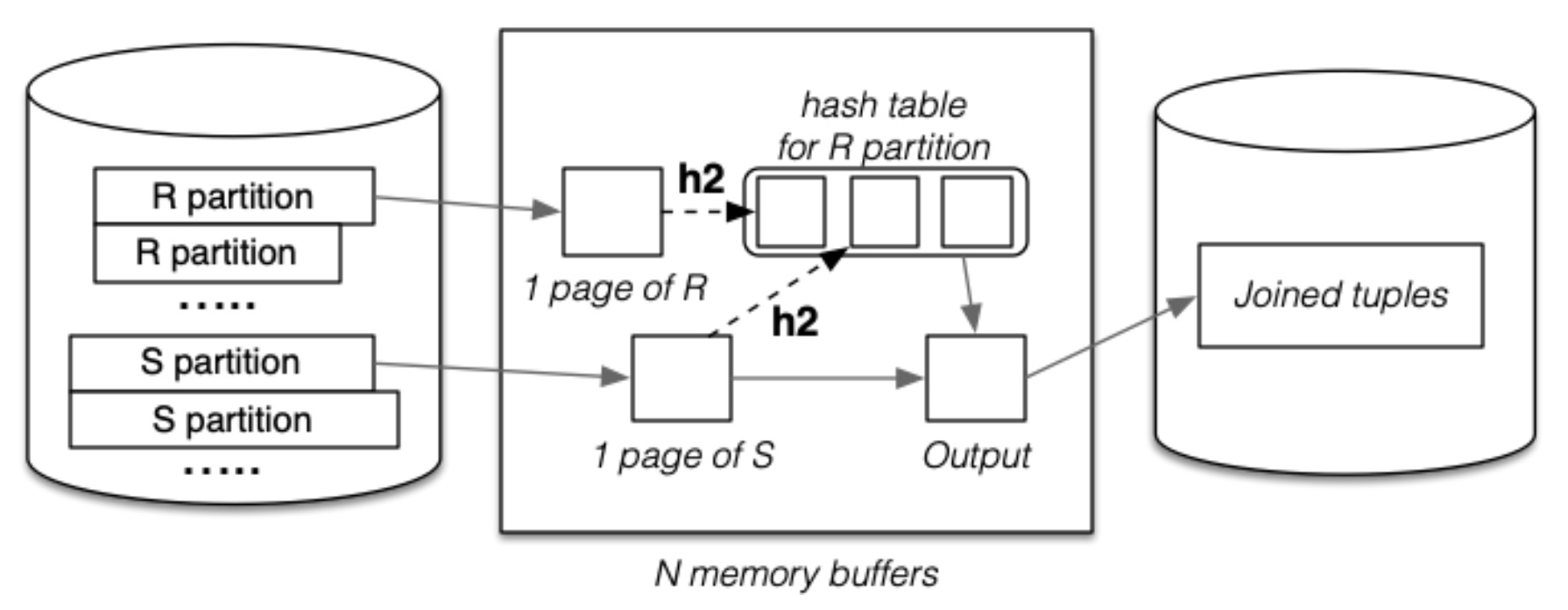
成本分析:
所有分区文件中的页面数量约为原文件页面数量(可能会稍多一些)。所以在进行分区时:
- 关系 R 的分区:\(Cost = read(b_R) + write(\approx b_R) = 2b_R\)
- 关系 S 的分区:\(Cost = read(b_S) + write(\approx b_S) = 2b_S\)
在 Join 阶段中,需要扫描所有的分区文件,\(Cost = b_R + b_S\)。由于所有的哈希和比较操作都在内存中进行,所以代价忽略不计。
因此:\(Cost_{total}=2b_R+2b_S+b_R + b_S=3*(b_R + b_S)\)
练习:Grace Hash Join 的成本
现在执行 \(Join_{[i=j]}(R,S)\),一些参数如下:
- \(r_R=1000,b_R=50,r_S=3000,b_S=150,c_{Res}=30\)
- \(R.i\) 是主键,关系 R 的每一个元组都有 2 个匹配的 S 元组
- 数据库管理系统有 \(N=43\) 个缓冲区
- 数据和哈希都符合均匀分布
使用 Grace Hash Join,假设关系 R 的分区都没有大于 40 个页面。计算页面读写次数和 Join 检查次数。
读页面次数为 \(Cost_{total}=3*(b_R+b_S)=3*(50+150)=600\),写页面次数同上个练习的分析,为 67 个页面。
使用 Grace Hash Join,假设关系 R 的分区有一个为 50 个页面,关系 S 对应的分区为 30 个页面,其余都没有大于 40 个页面。计算页面读写次数和 Join 检查次数。
Hybrid Hash Join
Hybrid Hash Join 是 Grace Hash Join 的一个变体。该方法的主要思路是如果有数量很多的缓冲区 \(\sqrt{b_R}<N<b_R+2\),那么应该如何利用这些富余资源。
此时同样进行分区,得到 \(k<<N\) 个分区,只是不再把所有的分区都写入磁盘,而是留一个分区在内存中,剩余的 \(k - 1\) 个写入磁盘。对于 \(N\) 缓冲区,有 1 个作为输入缓冲区,\(k-1\) 个输出缓冲区,\(p = N - k - 2\) 个用来存储那一个放在内存的分区。当对关系 R 进行扫描和分区时,所有哈希值为 0 的元组可以使用内存中的分区来进行解析。其他的元组会写到关系 R 的 \(k\) 个分区之一。最后的 Join 阶段与 Grace Hash Join 基本一致,但是只有 \(k - 1\) 个分区。
第一个阶段:首先对关系 R 进行分区,所有哈希值为 0 的元组都被放入内存分区中,其余存入磁盘。
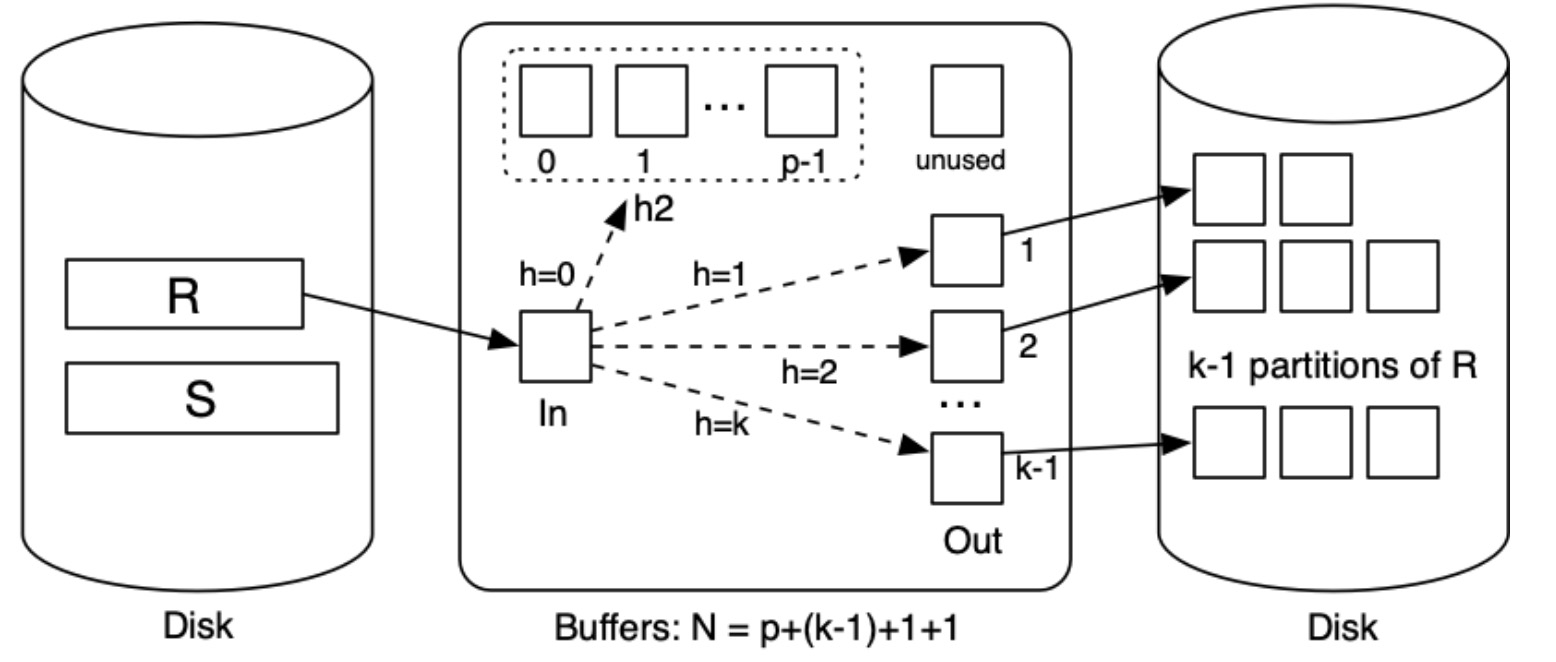
第二个阶段:对关系 S 进行分区,如果元组的哈希值为 0,那么就在内存分区寻找合适的元组,一旦寻找到匹配的元组,进行 Join,存入输出缓冲区中。在这一阶段中,我们得到了一部分结果:
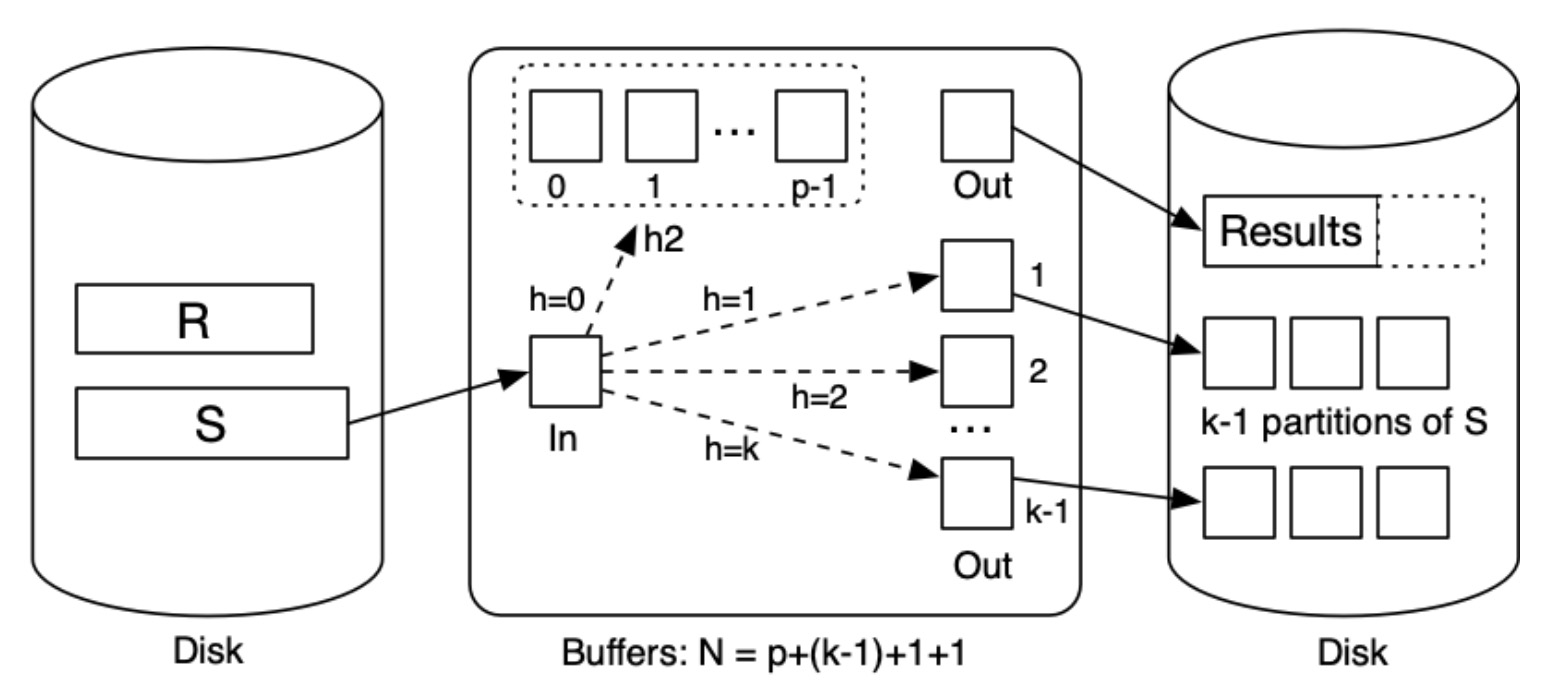
第三个阶段:对于剩下的这部分分区,使用和 Grace Hash Join 同样的方法进行处理,得到最后的结果。
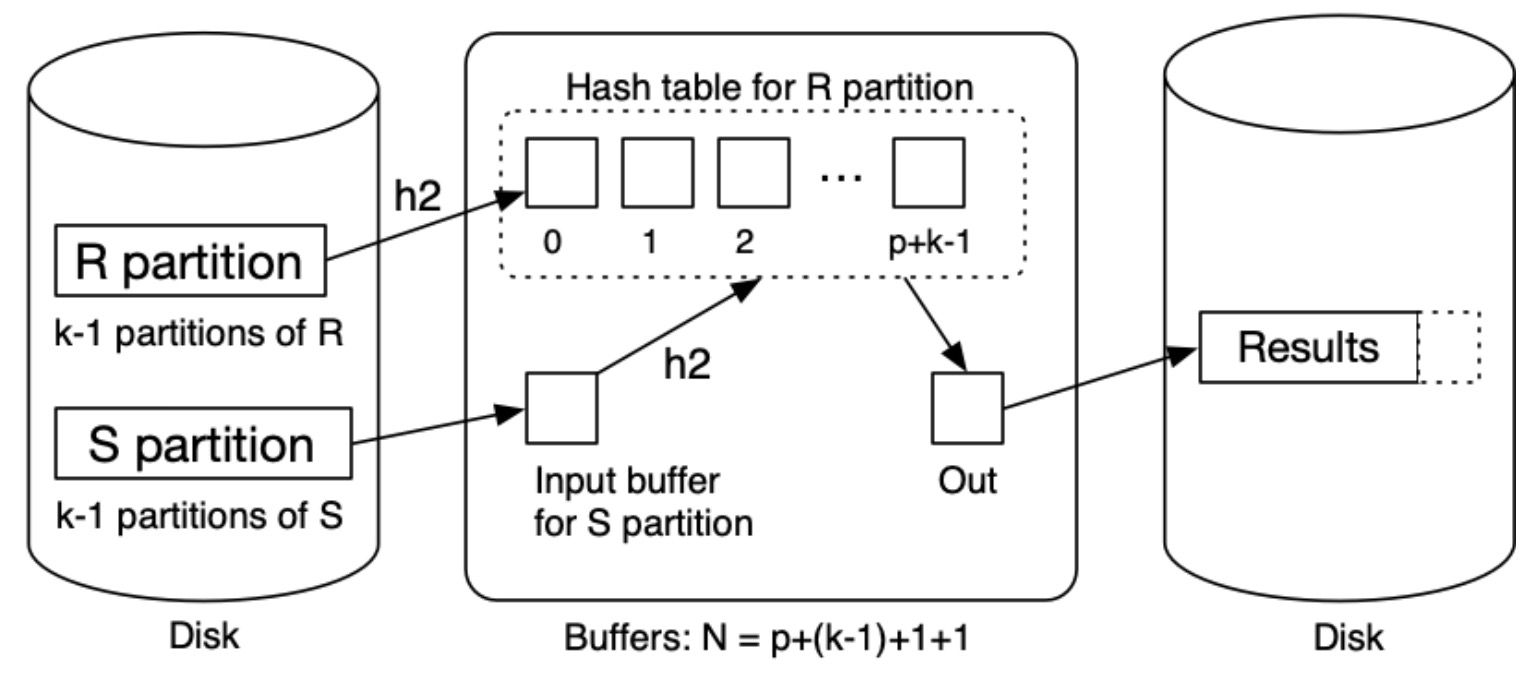
一些观察:
- 对于 \(k\) 个分区,每个分区的尺寸约为 \(\lceil\frac{b_R}{k}\rceil\)
- 将一个分区存在内存中,需要 \(\lceil\frac{b_R}{k}\rceil\) 个缓冲区
- 对于内存分区空间和分区的数量需要有所权衡
- 如果 \(N=b_R - 2\),使用 Nested Loop 会更简单,\(Cost\) 取决于 \(N\),但是少于 Grace Hash Join
练习
考虑一个如下所示的 SQL 查询:
select E.subj, S.name
from Student S join Enrolled E on (S.id = E.stude)
order by E.subj;
此时数据库的相关数据为:
\(r_S = 20000, c_S = 20, b_S = 1000\)
\(r_E = 80000, c_E = 40, b_E = 2000\)
现在有 \(N=103\) 个 缓冲区,我们来考虑 Join 的 代价:
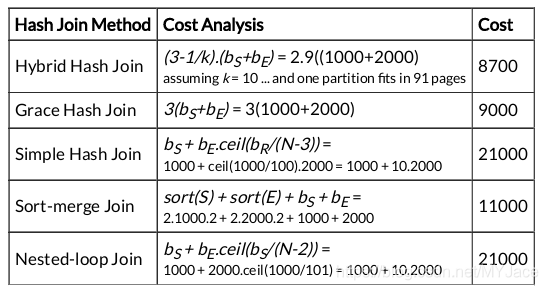


 浙公网安备 33010602011771号
浙公网安备 33010602011771号