数据库内核：PostgreSQL 索引

索引（Indexing）

索引分类

索引就是 \((keyVal,tupleID)\) 对构成的文件。

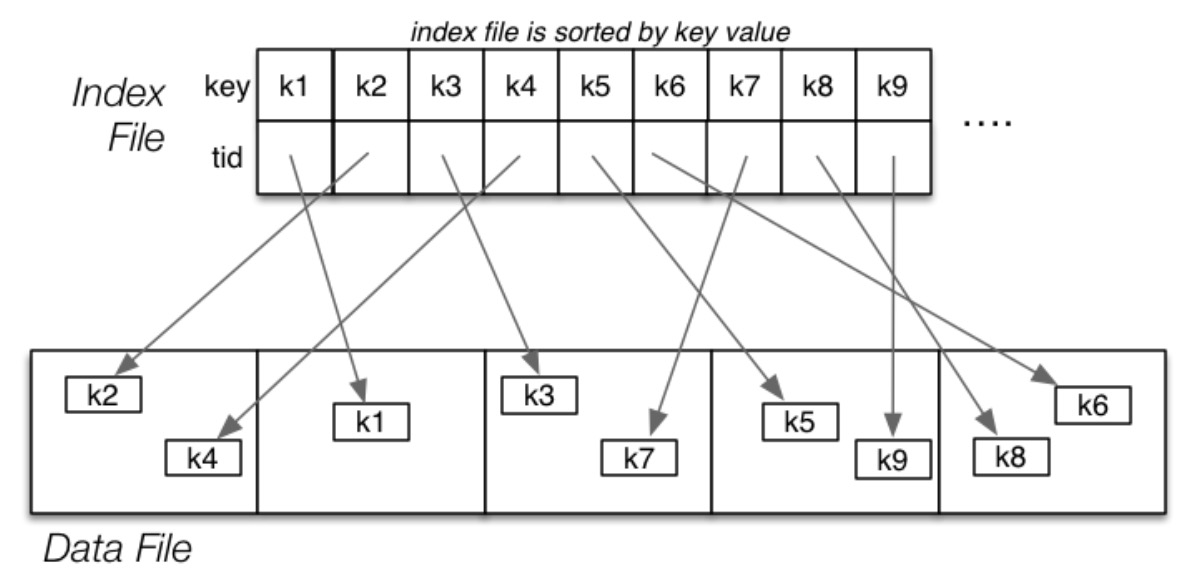
一维索引是基于单个属性值 A，这个属性有可能是数据文件的排序键，有可能其取值是不重复的。因此，基于索引属性种类可以将索引类型进行分类：

• Primary：属性 A 的取值是不重复（主键），且数据文件可能基于其进行排序的
• Clustering：属性 A 的取值有重复 (非主键)，但是数据文件一定是基于其排序的
• Secondary：数据文件不基属性 A 进行排序

一张表可能会有分别基于多个不同属性的多个索引文件。

索引构造方式

索引的构造方式有：

• Dense：每个元组都由索引文件中的条目引用
• Sparse： 只有一部分元组由索引文件中的条目引用
• Single-level：元组通过索引文件直接访问
• Multi-level：可能需要访问几个索引页面才能得到元组

因此，索引会有 \(i\) 个页面，显然这里的 \(i\) 一定远远小于数据文件中的 \(b\) 个页面。而索引文件的每个页存储元组的容量为 \(c_i\) (\(c_i>>c\))。

• Dense index：\(i=ceil(\frac{r}{c_i})\)
• Sparse index：\(i=ceil(\frac{b}{c_i})\)

Primary Index

Dense Primary Index

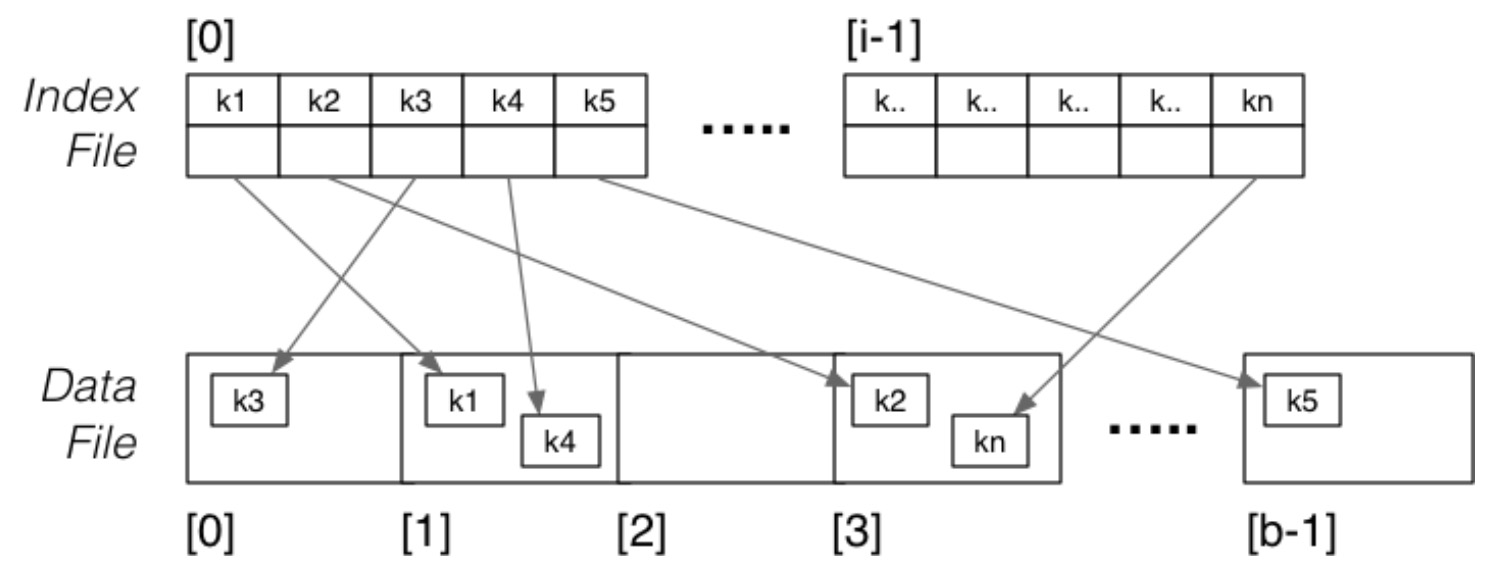
数据文件是未排序的，每个元组对应一个索引实体。

Sparse Primary Index

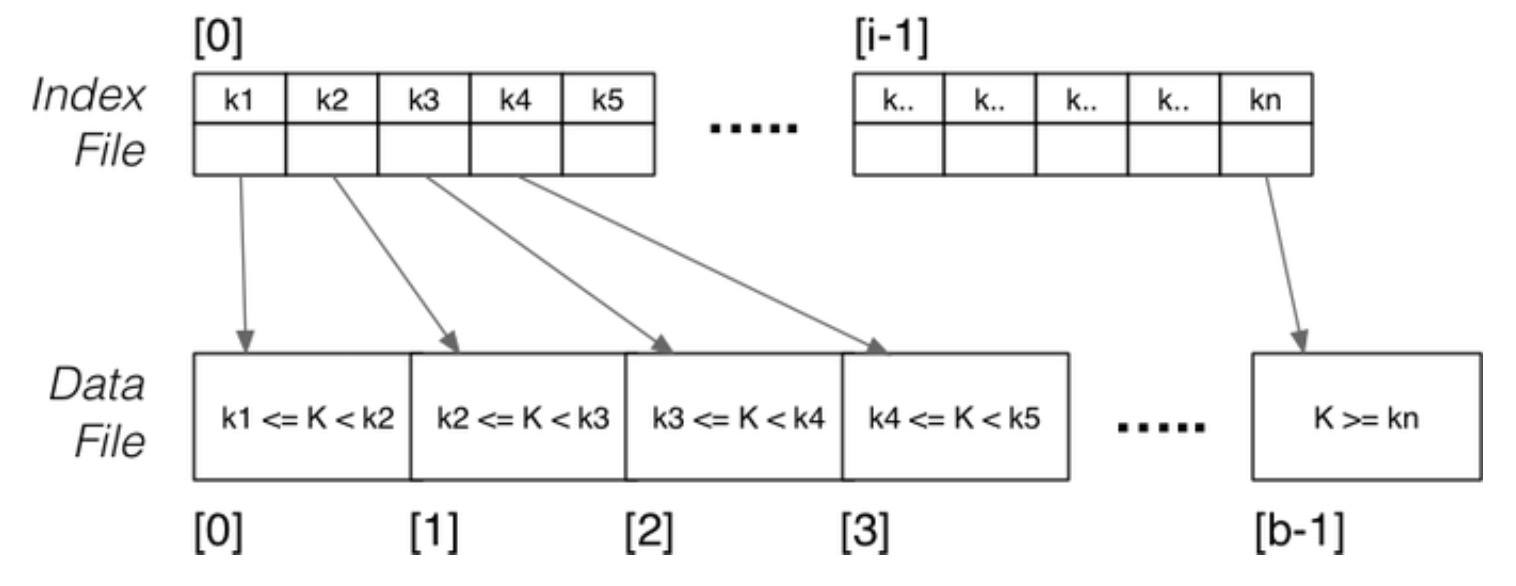
数据文件是排序的，每一个页面对应一个索引实体。

练习

一张关系表的参数如下：

• \(B=8192,R=128,r=100000\)
• 数据页面的头部信息占 \(256\) 字节
• 键是整数，数据文件按照该键排序
• 索引实体 \((keyVal,tupleID)\) 每个为 \(8\) 字节
• 索引页面的头部信息占 \(32\) 字节

问：Dense Index 需要多少个页面，Sparse Index 需要多少个页面？

每个页面大小为 \(8192\) 字节，索引头部占 \(32\) 字节，除去之后，剩余 \(8160\) 字节，每个索引实体又占 \(8\) 字节 ，所以索引页面可以存在 \(c_i=\frac{8160}{8}=1020\) 个索引实体。

数据页面的头部信息占 \(256\) 字节，除去之后，剩余 \(7936\) 字节，平均每个元组占 \(R=128\) 字节，因此数据页面可以存 \(c=\frac{7936}{128}=62\) 个元组，一共有 \(r=100000\) 个元组，所以需要 \(\lceil\frac{100000}{62}\rceil=1613\) 个页面。

Dense Index 需要 \(i=ceil(\frac{r}{c_i})=\lceil\frac{100000}{1020}\rceil=99\) 个页面

Sparse Index 需要 \(i=ceil(\frac{b}{c_i})\lceil\frac{1613}{1020}\rceil=2\) 个页面

Primary Index 中的选择

对于 One Typle Query，伪代码如下：

ix = binary search index for entry with key K
if nothing found { return NotFound }
b = getPage(pageOf(ix.tid))
t = getTuple(b,offsetOf(ix.tid))
   – may require reading overflow pages
return t

成本分析：最坏情况情况就是读 \(log_2i\) 个索引文件，加上读一个页面和它的所有溢出页面。

假设索引文件的页面大小等于数据文件的页面大小，所以两者读取页面的成本相同。因此，最终成本为 \(Cost_{one,prim}=log_2i+1+Ov\)

对于 Range Query，其大致思路为：

1. 使用索引进行查找，找到下界
2. 顺序读取索引，直到找到上界
3. 累计一组要检查的 Bucket
4. 检查每个 Bucket 以找到匹配的元组

伪代码如下：

// e.g. select * from R where a between lo and hi
pages = {} results = {}
ixPage = findIndexPage(R.ixf,lo)
while (ixTup = getNextIndexTuple(R.ixf)) {
	if (ixTup.key > hi) break;
	pages = pages ∪ pageOf(ixTup.tid)
}
foreach pid in pages {
	// scan data page plus ovflow chain
	while (buf = getPage(R.datf,pid)) {
		foreach tuple T in buf {
			if (lo<=T.a && T.a<=hi)
			results = results ∪ T
} 	}	 }

对于 Partial Match Retrieve，其操作和 One Type Query 基本一致。 如果一个查询不涉及主键，那么此时索引不会带来任何帮助，只能线性扫描整个数据文件。

Primary Index 中的插入

大致流程：首先将元组插入到合适的页面 P 的位置上，得到该元组的 ID，之后在索引文件中找到新实体的合适位置，将新的索引实体 \((k, tid)\) 插入到该位置。伪代码如下：

tid = insert tuple into page P at position p
find location for new entry in index file
insert new index entry (k,tid) into index file

这里存在一个重要的问题就是插入索引实体后，要保持索引实体的顺序不被打破。可以在索引文件中引入溢出页面，或者将插入位置之后的索引实体往后移动。后者重新排列的方法平均需要读/写一般的索引页面。其成本为：\(Cost_{insert,prim}=(log_2i)_r+\frac{i}{2}(1_r+1_w)+(1+Ov)_r+(1+\delta)_w\)

• \((log_2i)_r\)：使用二分查找找到新的索引实体应该被放置的索引页面的成本
• \(\frac{i}{2}(1_r+1_w)\)：重新排列所需的读/写一半的索引页面的成本
• \((1+Ov)_r\)：读取对应数据页面及其溢出页面以找到合适的插入位置的成本
• \((1+\delta)_w\) ：将更新后的页面写回磁盘的成本。这里的 \(\delta\) 可以是 \(0、1、1 + Ov\)

Primary Index 中的删除

大致流程：首先需要使用索引找到目标元组，之后将该元组标记为 “已删除”，最后将索引文件中对应该元组的索引实体删除。伪代码如下：

find tuple using index
mark tuple as deleted
delete index entry for tuple

而在删除索引实体时，同样也有两种选择，一个是进行标记，另一个就是进行重排。这两者的成本分别为：

• 标记：\(Cost_{delete,prim}=(log_2i)_r+(1+Ov)_r+1_w+1_w\)
• 重排：\(Cost_{delete,prim}=(log_2i)_r+(1+Ov)_r+\frac{i}{2}(1_r+1_w)+1_w\)

Clustering Index

数据文件是排序的，每个键值对应一个索引实体。

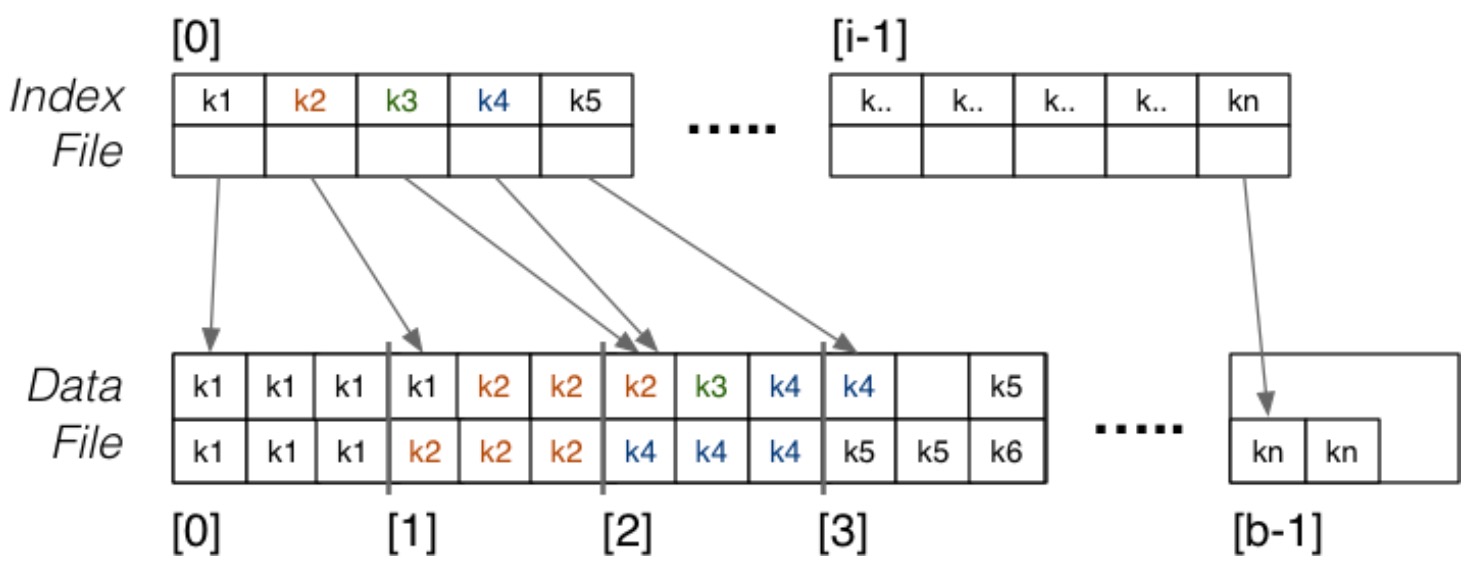
此时的索引不再基于主键。因此，此时的属性 A 会有重复的取值，索引文件中的每个实体只会指向重复取值的第一个页面。

此时的删除操作需要格外注意，因为具备相同键值的元组会有多个，因此必须等所有这些元组都被删除后，才能把索引文件中的对应索引实体删除。

Secondary Index

数据文件不是顺序的，同时属性 A 也不是主键。

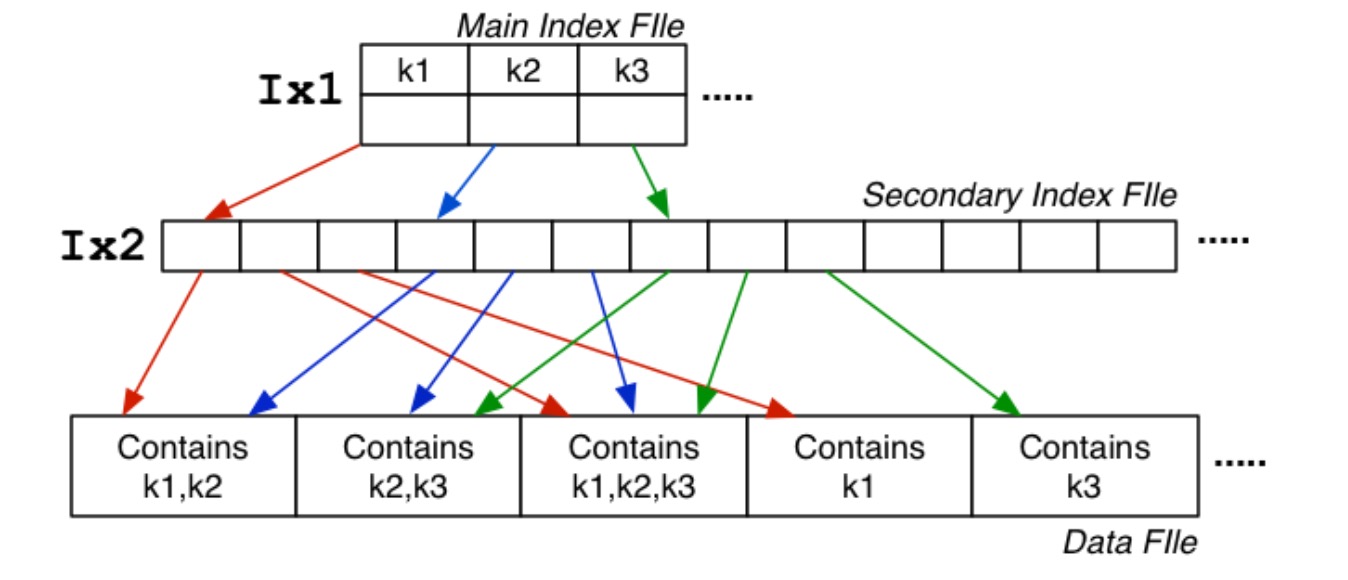
在上图中属性 A 有三种不同的取值，Main Index File 是这三种取值的索引，而 Secondary Index 则更进一步，对这三种取值的具体元组进行索引，在 3 个不同页面中具有 k1 取值的元组被 Secondary Index 索引了（红色）。 所以，当我们查询元组时，需要先搜索 Main Index File，然后再根据 Secondary Index 去找到元组的具体位置。其代价为：\(Cost_{pmr}=log_2i_{ix1}+a_{ix2}+b_q(1+Ov)\)

• \(log_2i_{ix1}\)：在 Main Index 中进行二分法搜索的成本
• \(a_{ix2}\)：在 Secondary Index 的连续页面中线性搜索的成本
• \(b_q(1+Ov)\)： 数据文件中那些包含目标元组的页面及其溢出页面搜索的成本

Multi-level Indexes

Secondary Index 使用两个索引文件可以提升搜索的效率，其中 \(b_{ix1} << b_{ix2} << b\)。这种方法还可以进一步提升。比如，可以把 \(ix1\) 变为 Sparse Index，因为 \(ix2\) 一定是有序的，此时 \(b_{ix1} = \lceil(\frac{b_{ix2}}{c_i})\rceil\)。Secondary index 是 Multi-level Index 的基本形式，可以增加更多的索引文件，但是一定要保证最顶层的索引是最小的，极限情况下，顶层索引可以只有一个页面，以下是一个三层索引的例子：

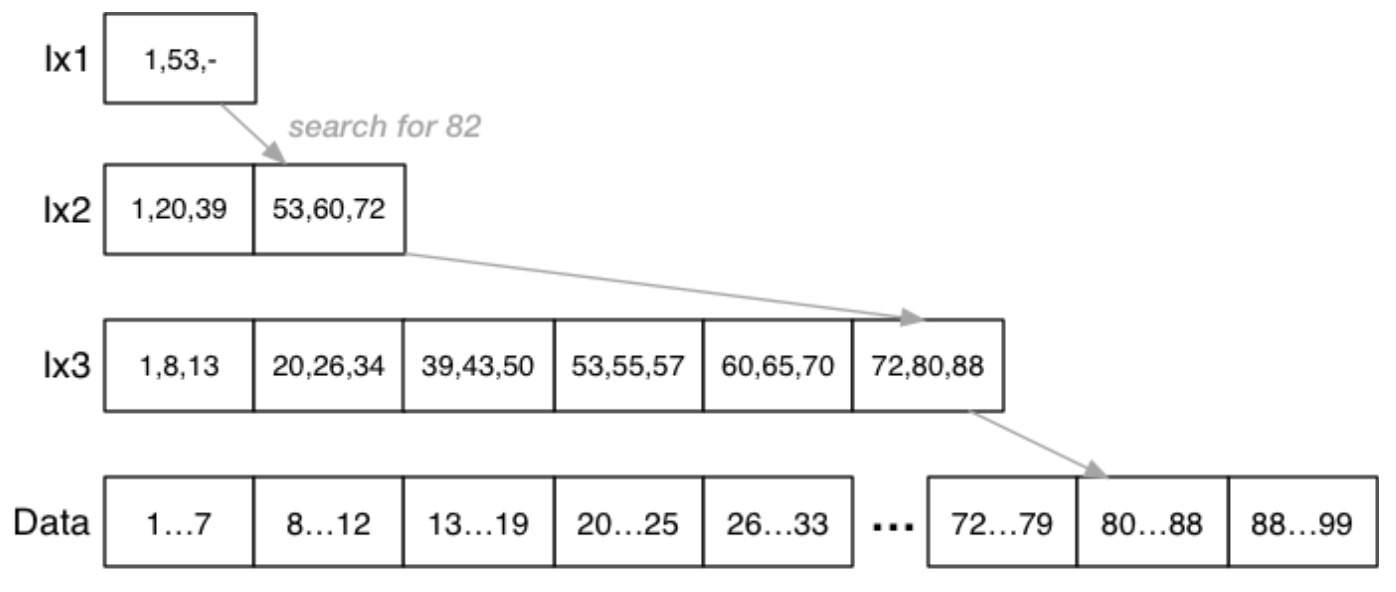
Multi-level Indexes 的选择

对于 One Type Query，其伪代码如下：

xpid = top level index page
for level = 1 to d {
	read index entry xpid
	search index page for J'th entry
		where index[J].key <= K < index[J+1].key
	if (J == -1) { return NotFound }
	xpid = index[J].page
}
pid = xpid // pid is data page index
search page pid and its overflow pages

成本分析：\(Cost_{one,mli}=(d+1+Ov)_r\)，这里的 \(d=\lceil log_{c_i}r\rceil\)，因为索引实体所占空间很小，索引 \(c_i\) 很大。

B-Trees

B 树简介

B 树是一个具有以下属性的多路搜索树：

• 它们进行更新时仍保持平衡
• 每个节点中至少有 \(\frac{n-1}{2}\) 个实体
• 每个树节点占据一整个磁盘页面

B 树插入和删除操作可以被很高效地实现，但是描述起来比较复杂。B 树相对于普通的多路搜索树具有以下优点：

• 更好的存储利用率（约有 \(\frac{2}{3}\) 是满的）
• 最坏情况下有更好的表现（树不高）

以下是 B 树的一个例子 \(depth=3,n=3\)，实际上是 B+ 树，与一般的 B 树不同的地方在于，B+树仅有左节点可以与数据页交互，而 B 树中的所有节点都可以与数据页交互：

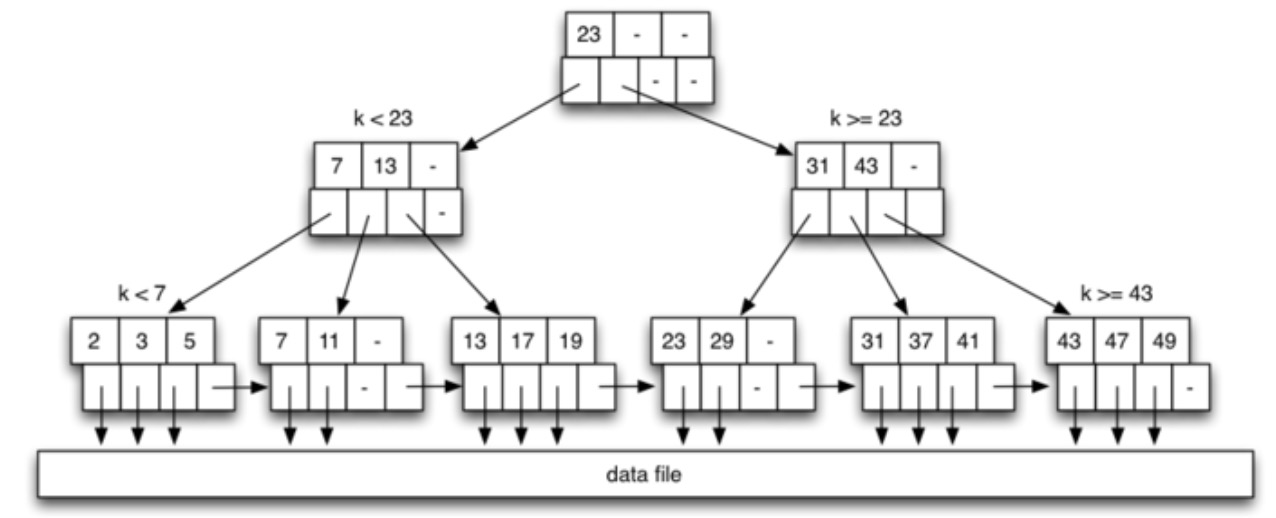
每个节点中，上半部分是键，下半部分是指针，根据条件指向不同的节点。在数据库中，节点就是页面。

B 树的深度

树的深度取决于有效的分支因子，即每个节点的满载程度。研究表明，一般的 B 树节点满载程度为 69% 左右。所以，负载 \(L_i=0.69*c_i\)，树的深度约为 \(\lceil log_{L_i}r\rceil\)。

B 树选择

对于 One Type Query，使用 B 树进行搜索只需要从根节点开始向下搜索，直到在某个叶节点找到满足要求的结果。其伪代码如下：

N = B-tree root node
while (N is not a leaf node)
   N = scanToFindChild(N,K)
tid = scanToFindEntry(N,K)
access tuple T using tid

成本为 \(Cost_{one}=(D+1)_r\)

对于 Range Query，对范围的下界进行树搜索，再得到某个叶节点之后，通过叶节点之间的联系（指针）向后继续搜索，直到找到上界。其伪代码如下：

search index to find leaf node for Lo
for each leaf node entry until Hi found {
		access tuple T using tid from entry
}

成本为 \(Cost_{one}=(D+b_i+b_q)_r\)

举个例子，现在执行 SELECT * FROM Relation r WHERE r.id ≥ 11 AND r.id < 25;，此时的 B 树如下所示：

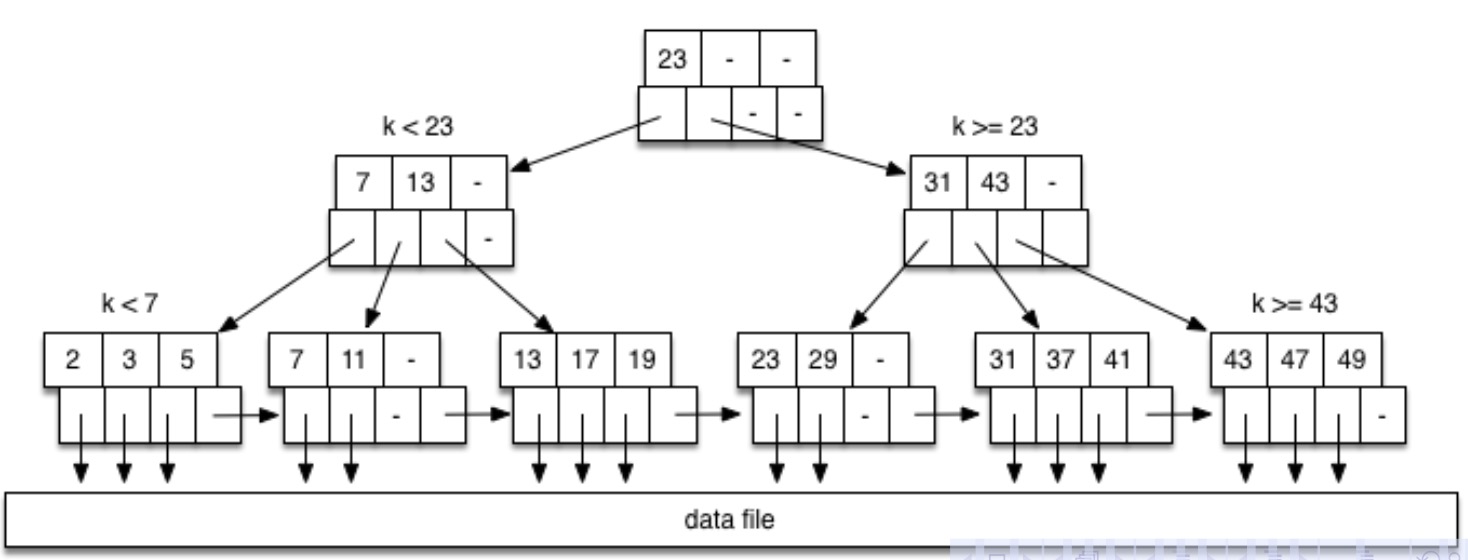
先搜索下界 11，此时到达第二个叶节点，在其中找到 11 之后，向后继续搜索下一个（右边）的叶节点，直到找到上界（第四个叶节点）。

B 树的插入

插入的大致流程：

1. 找到合适的叶节点和该叶节点中适合存放新键值的位置
2. 如果该节点未满，就直接将新键值插入
3. 如果该节点已满：
   1. 将中间元素提升为父元素
   2. 把该节点分割为两个半满节点
   3. 把新键值插入到合适的半满节点中
4. 如果父节点也满了，那就继续分割，向上操作（同上）
5. 如果已经到了根节点，并且根节点也没有空闲的位置了，那就向上创建一个新的根节点

例子：在下图的 B 树中插入 12, 15, 30, 10：

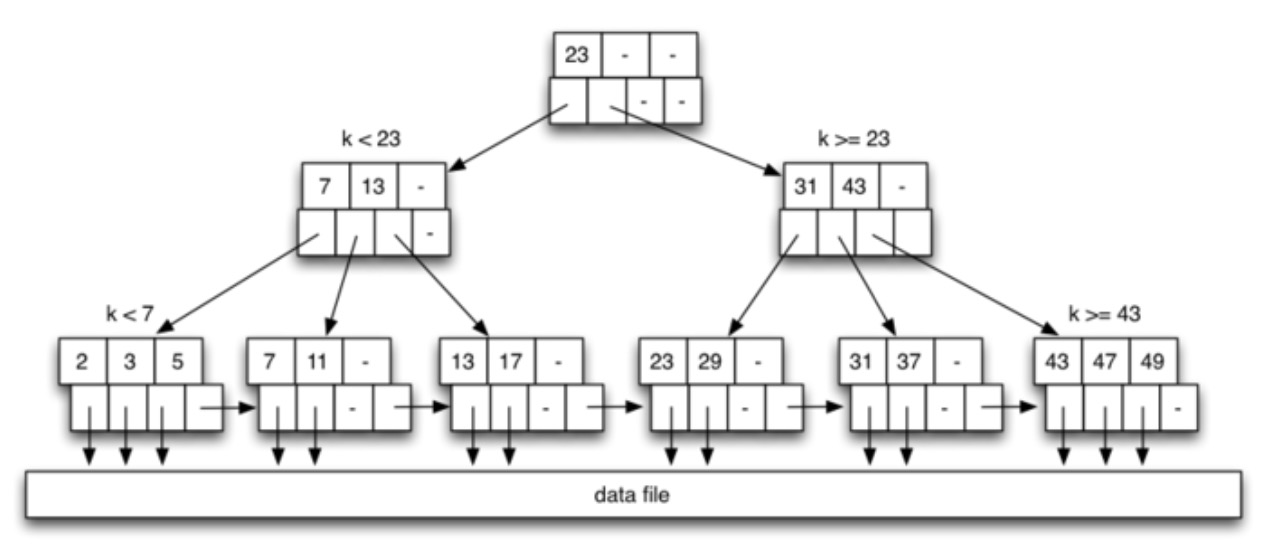
首先插入 12，从根节点开始搜索，找到第 2 个叶节点，该节点存在空闲空间，所以直接将 12 插入。接这插入 15，找到第 3 个叶节点，该节点存在空闲空间，所以直接将 15 插入，为了保证索引页面（节点）中的顺序不被打破，将其插入在 13 和 17 之间。再接着插入 30，找到第四个叶节点，该节点存在空闲空间，所以直接将 30 插入。插入前三个数之后，B 树如下所示：

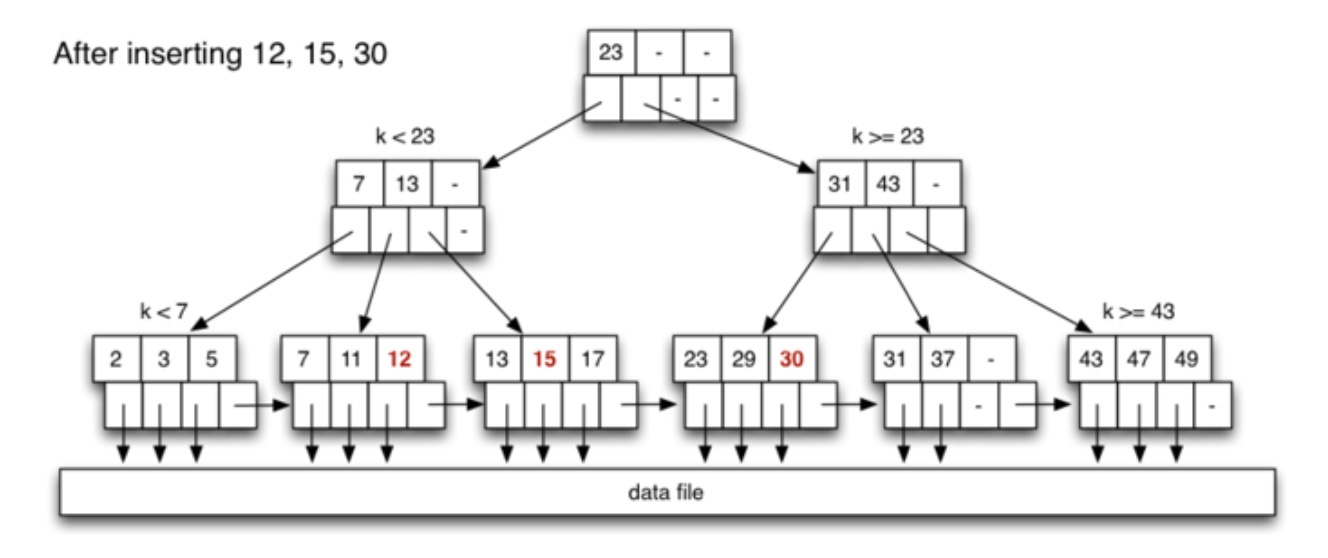
最后插入 10，同样先找到合适的叶节点，第 2 个叶节点，此时该节点已经满了，因此需要进行分割。将该节点中的中间元素 11 写到父节点中，并将叶节点划分会两个叶节点，如下所示：

成本分析：\(Cost=Cost_{treeSearch}+Cost_{treeInsert}+Cost_{dataInsert}\)

最好的情况：只需要写一个页面，也就是从根节点找到叶节点后，有空闲的位置。其成本为 \(Cost_{insert}=D_r+1_w+1_r+1_w\)

一般的情况：3 个节点需要写（两个半满节点+一个父节点），也就是从根节点开始遍历，把遍历的节点保存在缓冲区中，找到叶节点后，先读/写数据页面，再更新/写叶节点和父节点。其成本为 \(Cost_{insert}=D_r+3_w+1_r+1_w\)

最坏的情况：有 \(2D-1\) 个节点需要写（传播到根节点），也就是从根节点遍历到叶节点，读/写数据页面。更新/写叶节点和父节点，重复该操作 \(D-1\) 次。其成本为 \(Cost_{insert}=D_r+3D_w+1_r+1_w\)，优化后的成本为 \(Cost_{insert}=D_r+(2D-1)_w+1_r+1_w\)

PostgreSQL 中的 B 树

PostgreSQL 中的 B 树叫作 Lehman/Yao-style B-trees。是一个能在高并发环境下高效工作的变体。

• 实现在 backend/access/nbtree 目录下
• 存储所有相等键的实例（dense index）
• 在键等于页面中的最大键时进行右侧扫描以避免分裂
• 常见的插入情况是新键是整个数据结构中的最大键，可以高效地处理

在 PostgreSQL 版本 12 中有以下变化：

• 索引实体更小：为了复合键，只存储第一个属性，索引实体更小，因此 \(c_i\) 更大，因此树更浅。
• 在索引键中包含 TID：重复的索引条目按照“表顺序”存储，这使得扫描表文件以收集结果更有效。

N-dimensional Queries

多维查询简介

一维查询，例如 select * from R where a = K; 和 select * from R where a between Lo and Hi;，堆、哈希、索引都可作为高效实现的方式。

而多维查询通常会产生更少的结果，需要考虑更多的信息，成本也更高。

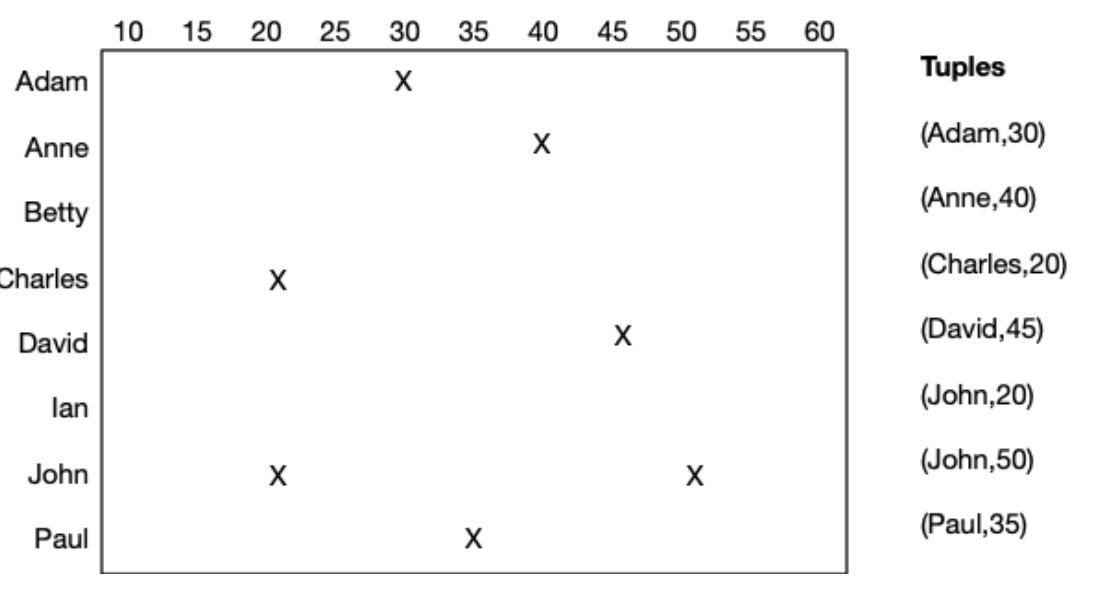
假设有一张如下的关系表：

create table Rel (
	X char(256),
	Y integer
);
# 样例元组就有：
# R(‘Adam’,30) R(‘Anne’,40) R(‘Charles’,20) R(‘David’,45)
# R(‘John’,20) R(‘John’,50) R(‘Paul’,35)

由上面的关系表可以得到元组空间，如下所示：

多维查询就是选择的条件中存在多余一个以上的属性，它又分为两种类型：

• Partial-Match Retrieval（PMR）：select * from Person where name = ’John’ and age = 50;
• Tuple-Space Queries（Space）：select * from Person where 20 ≤ age ≤ 50 and ’Charles’ ≤ name ≤ ’John’

通过 Heap 实现多维查询

对于 Heap file 可以通过标准方法来处理 PMR 和 Space 查询。其伪代码如下：

// select * from R where C
r = openRelation(”R”,READ);
for (p = 0; p < nPages(r); p++) {
		buf = getPage(file(r), p);
		for (i = 0; i < nTuples(buf); i++) {
				t = getTuple(buf,i);
				if (matches(t,C))
    				add t to result set
    } 
}

这种方法都是将数据页面按顺序都遍历了一遍，所以对两类查询的成本都一样 \(Cost_{pmr}=Cost_{space}=b\)。

通过 Multiple Indexes 实现多维查询

现在的数据库管理系统已经支持对一张表建立多个索引了。要构建哪些索引取决于查询。

create table R (a int, b int, c int);
create index Rax on R (a);
create index Rbx on R (b);
create index Rcx on R (c);
create index Rabx on R (a,b);
create index Racx on R (a,c);
create index Rbcx on R (b,c);
create index Rallx on R (a,b,c);

但是多个索引就需要更多的空间，以及数据更新时对索引的维护成本。

从广义角度来看，PMR 和 Space 查询就等价于以下 SQL：

select * from R
where a1 op1 C1 and...and an opn Cn;

• PMR：\(op_i\) 为等于
• Space：\(op_i\) 为范围

除了广义角度，对于多维查询还有以下可行的方法：

• 对某一个属性 \(a_i\) 建立索引，减少元组测试
• 对所有属性都建立索引，结果就是他们的交叉集

如果只使用一个索引，应该选择索引 \(a_i\)，经过 ai opi Ci 条件可以得到匹配的元组数量最少。

• 假设 \(a_i\) 属性值在其范围内是均匀分布的
• 主键的相等测试最多给出一个匹配
• 如果 \(a_i\) 属性值的范围是最广的，那么对于相等测试，其匹配的结果数量最少
• 如果 \(a_i\) 属性值的范围是最广的，那么对于范围测试，其匹配的结果数量最多

只使用一个索引的查询伪代码如下：

// Query:select*fromRwhere a1 op1 C1 and ... and an opn Cn; 
// 假设对 ai 建立索引最好
TupleIDs = IndexLookup(R,ai,opi,Ci)
//gives{ tid1 , tid2 ,...} for tuples satisfying ai opi Ci 
PageIDs = { }
foreach tid in TupleIDs
{ PageIDs = PageIDs ∪ {pageOf(tid)} }
// PageIDs = a set of b q ix page numbers ...

其成本为 \(Cost=Cost_{index}+b_{q_{ix}}\)，根据某个条件得到的结果页面集中有些页面不包含最终答案，因此 \(b_{q_{ix}}>b_q\)，DBMS 通常维护统计数据，以帮助确定选择哪个属性建立索引。

使用多个索引的查询伪代码如下：

// Query:select*fromRwhere a1 op1 C1 and...and an opn Cn;
// 假设 ai 是下标最小的一个索引
TupleIDs = IndexLookup(R,a1,op1,C1)
foreach attribute ai with an index {
		tids = IndexLookup(R,ai,opi,Ci)
		TupleIDs = TupleIDs ∩ tids 
}
PageIDs = { }
foreach tid in TupleIDs
{ PageIDs = PageIDs ∪ {pageOf(tid)} } 
// PageIDs = a set of b q page numbers

其成本为 \(Cost=kCost_{index}+b_q\)，这里的 \(k\) 就是索引的数量。

练习

现在有一张关系表，\(r=100000,B=4096\)，关系表的模式如下：

create table Students (
    id       integer primary key,
    name     char(10), – simplified
    gender   char(1),  – ’m’,’f’,’?’
    birthday char(5)   – ’MM-DD’
);

• 数据文件没有按照任意一个属性进行排序
• 对每一个属性都有一个 dense index
• 每一个数据页面或者索引页面的头部信息都占 \(96\) 字节

问题 1：计算数据文件和每个索引文件的大小

• id：整数类型，为 4 个字节
• name：字符类型，长度为 10 个字符，每个字符通常占用 1 个字节，共 10 个字节
• gender：共 1 个字节
• birthday：共 5 个字节

因此一个元组占 20 个字节。一个页面 4096 字节，去掉头部信息的 96 个字节，剩余 4000 个字节，可以存储 \frac{4000}{20}=200 个元组。因此数据文件有 \(\frac{100000}{200}=500\) 个页面，总大小为 \(500*4096=2048000\) 字节。

id 属性的索引：该属性为 4 个字节，因此索引实体为 4 字节，一个索引页面可以存储 \(\frac{4000}{4}=1000\) 个索引元组，需要 \(\frac{100000}{1000}=100\) 个页面，因此该索引文件的总大小为 \(100*4096=409600\) 字节。

其他属性同上，不再赘述，（不确定索引实体是否直接等于属性的大小，因为没有多余的信息）。

问题 2：描述每个属性的选择性

对于相等测试：\(id>name>birthday>gender\)

对于范围测试：\(id<name<birthday<gender\)

问题 3：现在执行 select * from Students where name=’John’ and birthday=’04-01’; SQL 语句，估计使用不同索引的成本。

• 只使用 name 索引，其成本为 \(Cost=Cost_{nameIndex}+b_{q_{John}}\)
• 只使用 birthday 索引，其成本为 \(Cost=Cost_{birthdayIndex}+b_{q_{04-01}}\)
• 同时使用上面两个索引，其成本为 \(Cost=Cost_{nameIndex}+Cost_{birthdayIndex}+b_q\)

Bitmap Indexes

Bitmap Indexes 的介绍

还有一种索引结构就是 Bitmap Indexes，它只专注于一组元组：

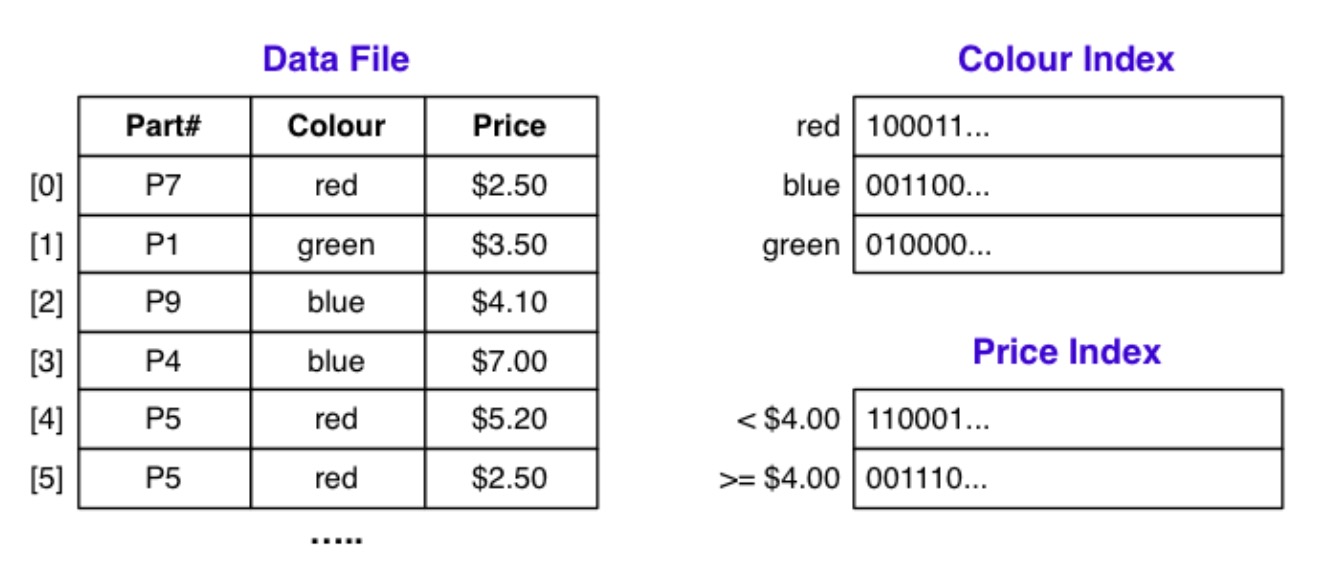
索引实体包含 \(r\) 比特的比特字符串，因为有 \(r\) 个元组，以颜色索引中 red 实体，其值为 \(100011..\)，这就表示第一个元组的颜色为红色，第二个不是红色，以此类推。还有一个 tids 文件，对应于每一个元组：

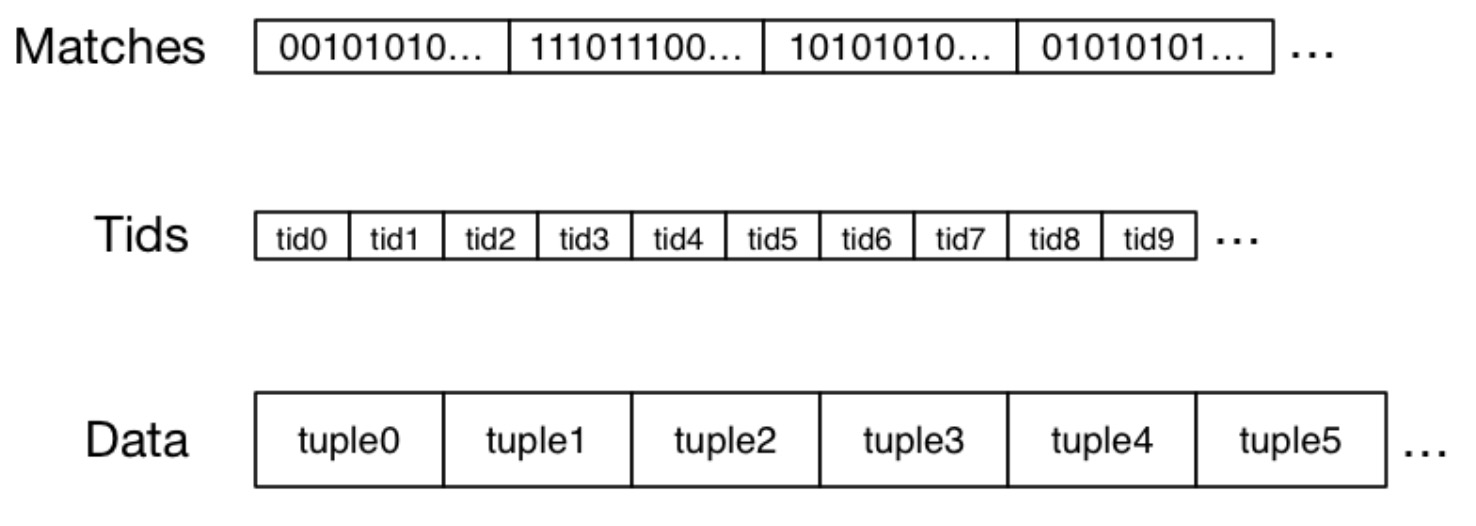
使用 bitmap index 进行查询的伪代码如下：

Matches = AllOnes(r)	// 将所有位设置为1，表示初始阶段元组都”符合“
foreach attribute A with index {
		// 根据与WHERE子句中A相关联的值选择第i个位串（即Bitmaps[A][i]）
  	// 并将其与Matches进行按位与操作。这将导致Matches中只有满足所有WHERE条件的元组对应的位被设置为1。
  	Matches = Matches & Bitmaps[A][i]
}
// 通过遍历0到r-1的索引i，检查Matches中的每个元素，如果为0，则跳过该元素。
foreach i in 0..r-1 {
		if (Matches[i] == 0) continue; 
  	Pages = Pages ∪ {pageOf(Tids[i])}
}
foreach pid in Pages {
    P = getPage(pid)
    extract matching tuples from P
}

位图索引的存储成本：

• 每个索引属性的每个值/范围的一个位图
• 每个位图都有长度 \(\lceil\frac{r}{8}\rceil\)c 个字节

位图索引的查询执行成本：

• 为查询中的每个索引属性读取一个位图
• 按位与操作（在内存中执行）
• 读取包含匹配元组的页面

位图可以索引页面，不一定非要元组，这样形成的位图更小。

练习

文件结构如下所示：

问题：以下查询是如何进行的？

我以前 6 个元组进行说明，最开始 Matches=111111

• select * from Parts where colour=’red’ and price < 4.00;：首先将 Matches 与红色的索引值进行按位与操作，得到结果 \(100011\)，然后将这个中间结果与价格小于 4 的索引值进行按位与操作，即 100011 & 110001 = 100001 ，这就表示第一个元组和第六个元组是符合查询的。
• select * from Parts where colour=’green’ or colour =’blue’;：简单来说就是 111111 & 010000 = 010000，111111 & 001100 = 001100，前者符合条件的是第二个元组，将其加入到结果集中，后者符合条件的是第三和第四个元组，由于是或操作，就将两个结果集合进行并操作。

Hashing for N-d Selection

MA.Hashing

对于 PMR 查询 select * from R where a1=C1 and...and an=Cn;来说：

• 如果某个属性 ai 是哈希键，那么查询会非常高效
• 如果某个属性 ai 不是哈希键，那么就需要线性遍历

因此，我们可以使用多属性哈希（mah）来提高效率。首先，形成一个包含所有属性的复合哈希值，然后在查询时，复合哈希的某些组件是已知的，这就允许我们缩小要检查的页面数量。MA.hashing 与任何动态哈希方案配合使用。

MA.hashing 参数：

• 文件大小 \(b=2^d\) 个页面，所以使用 \(d\) 比特的哈希值
• 关系有 \(n\) 个属性：\(a_1,...,a_n\)
• 属性 \(a_i\) 的哈希函数是 \(h_i\)
• 属性 \(a_i\) 贡献了 \(d_i\) 位（构成哈希值）
• 总共比特数 \(d=\sum_{i=1}^nd_i\)
• 一个选择向量声明了 k 位哈希值，我们需要知道其中每一部分的地址

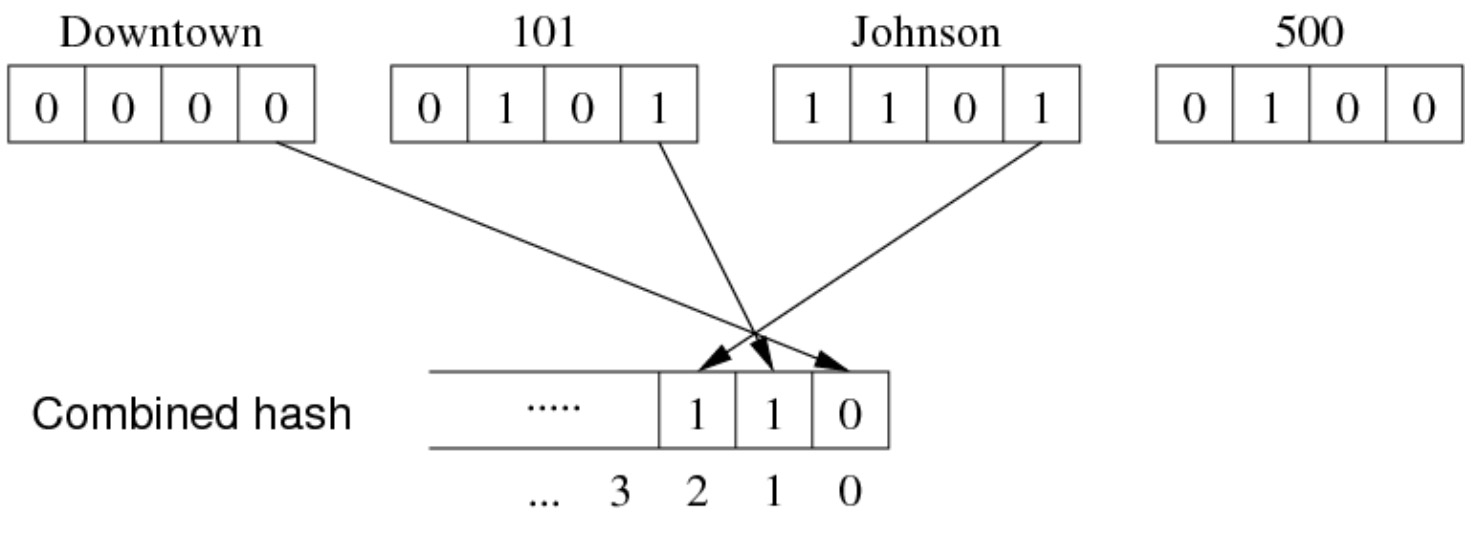
MA.hashing 的例子

有一个关系 Deposit(branch,acctNo,name,amount)，假设一个包含 8 个主要数据页（加上溢出页面）的小数据文件。哈希参数 \(d=3,d_1=1,d_2=1,d_3=1,d_4=0\)，这里忽略了 amount 属性，因为没有人会问 select * from Deposit where amount=533 这样的查询。

选择向量：

这个选择向量可以告诉我们以下信息：

• 哈希值中的 bit 0 来自 \(hash_1(d_1)\) 的 bit 0
• 哈希值中的 bit 1 来自 \(hash_2(d_2)\) 的 bit 0
• 哈希值中的 bit 2 来自 \(hash_3(d_3)\) 的 bit 0
• 哈希值中的 bit 3 来自 \(hash_1(d_1)\) 的 bit 1
• 以此类推

考虑一下这个元组：

复合哈希值（页面地址）的计算如下：

MA.Hashing 哈希函数

一些辅助定义：

# define MaxHashSize 32
typedef unsigned int HashVal;

// 提取哈希值第i比特
#define bit(i,h) (((h) & (1 << (i))) >> (i))
  
// 选择向量的元素
typedef struct { int attr, int bit } CVelem;
typedef CVelem ChoiceVec[MaxHashSize];

// 对单个属性的哈希函数
HashVal hash_any(char *val) { ... }

为元组 t 生成组合 d 比特的哈希值：

HashVal hash(Tuple t, ChoiceVec cv, int d)
{
		HashVal h[nAttr(t)+1];	// 用于存储每个属性的哈希值
    int i,a,b;
    for (i = 1; i <= nAttr(t); i++)
    		h[i] = hash_any(attrVal(t,i));	// 对每个属性值进行哈希计算
  	for (i = 0; i < d; i++) {
        a = cv[i].attr;	// 从选择向量中获取属性索引
        b = cv[i].bit;	// 从选择向量中获取位索引
        oneBit = bit(b, h[a]);	// 从属性的哈希值h[a]中提取第b位的值
        res = res | (oneBit << i);	// 将每个选择向量元素的oneBit值合并为最终的哈希值res
    }
		return res; 
}

练习：使用 MA.Hashing 的哈希函数计算元组 (’John Smith’,’BSc(CompSci)’,1990,99.5) 的哈希值。

• 哈希参数 \(d=6,d_1=3,d_2=2,d_3=1\)

• 选择向量为 \(cv=<(1,0),(1,1),(2,0),(3,0),(1,2),(2,1),(3,1),(1,3)...>\)

• \(hash_1(’John Smith’)=...0101010110110100\)

• \(hash_2(’BSc(CompSci)’)=...1011111101101111\)

• \(hash_3(1990)=...0001001011000000\)

选择向量第一个元素是 \((1,0)\) 表示选择第一个属性的哈希值的第 0 位，也就是 \(hash_1(’John Smith’)=...0101010110110100\) 中的 0。以此类推元组的哈希值为 \(110100\)

MA.Hashing 查询

对于 Partial Match Query，我们知道一部分属性的值，但是还有一部分未知。比如：

select amount
from Deposit
where branch = ’Brighton’ and name = ’Green’l;

此时我们知道 (Brighton, ?, Green, ?)。为了解决这类问题，我们首先来看一个更简单的问题：

select amount from Deposit where name=‘Green’;

此时我们只知道属性 name 的值为 Green，但是根据前面所说，我们需要构建一个复合哈希值，因此就有：

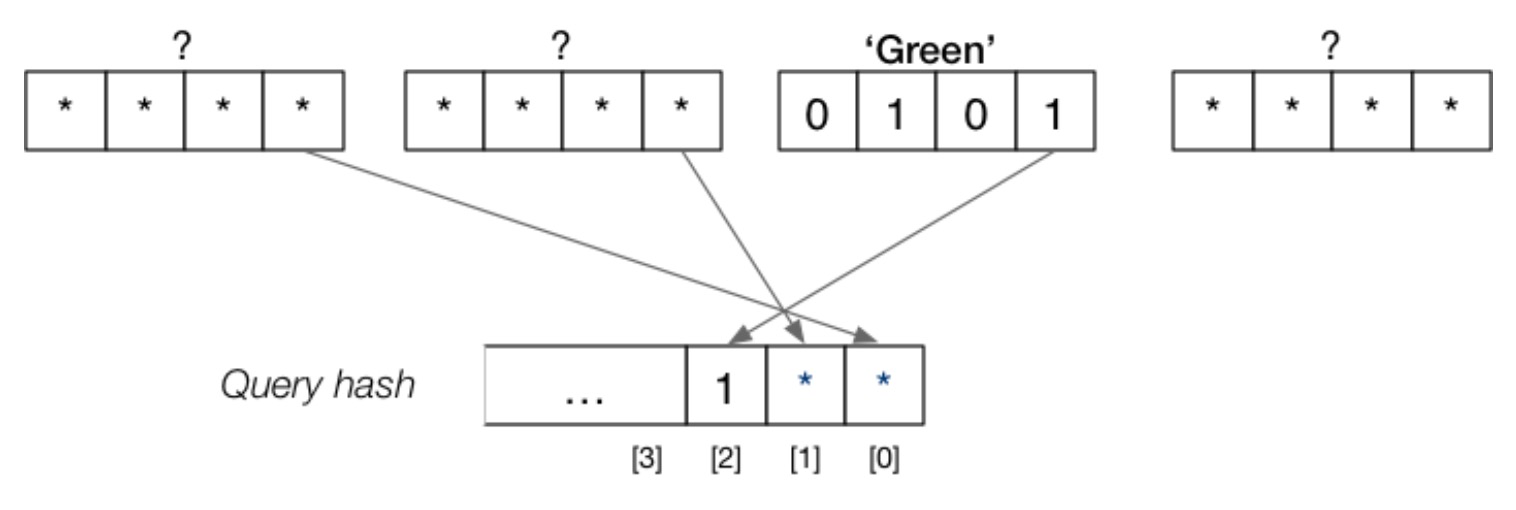
我们只知道复合哈希值的第 3 位是 1，因此，匹配的元组一定在 \(100,101,110,111\) 这几个页面中。

练习：\((a,b,c),(?,b,c),(a,?,?),(?,?,?)\) 这几个查询的部份哈希是什么？

• \(d=6,b=2^6,cv=<(0,0),(0,1),(1,0),(2,0),(1,1),(0,2),...>\)
• \(h(a)=...00101101001101\)
• \(h(b)=...00101101001101\)
• \(h(c)=...00101101001101\)

对于 \((a,b,c)\) 查询，哈希值为 \(101101\)

对于 \((?,b,c)\) 查询，哈希值为 \(*011**\)

对于 \((a,?,?)\) 查询，哈希值为 \(1***01\)

对于 \((?,?,?)\) 查询，哈希值为 \(******\)

MA.Hashing 查询算法的代码如下：

// 根据查询条件构建一个部分哈希值，并使用该部分哈希值找到候选页面。
// Treats query like tuple with some attr values missing
nstars = 0;
for each attribute i in query Q {	// 遍历查询Q的每个属性i
  	// 如果查询Q具有该属性的值（即属性值不为空），则使用选择向量和哈希函数计算属性值的哈希值，并将结果设置到组合哈希值中的相应位置。  
  	if (hasValue(Q,i)) {	
        set d[i] bits in composite hash
            using choice vector and hash(Q,i)
    } else {	// 如果查询Q缺少属性i的值（即属性值为空），则将相应位置的组合哈希值设置为*字符，并通过变量nstars跟踪字符的数量。
        set d[i] *’s in composite hash
            using choice vector
        nstars += d[i]
    }
} 

...
  
// 使用部分哈希值找到候选页面
r = openRelation(”R”,READ);
// 每次迭代时，将组合哈希值中的*字符替换为特定的值
for (i = 0; i < 2nstars; i++) {
    P = composite hash
    replace *’s in P
        using i and choice vector
    // 从关系R的文件中读取页面Buf，并对Buf中的每个元组T进行遍历。
    Buf = readPage(file(r), P);
    for each tuple T in Buf {
        if (T satisfies pmr query)
            add T to results
		} 
}

练习：将未知信息重新表示，MA.Hashing 引入了第三个值 \(*\)，这个符号表示未知。对于得到的复合哈希值 \(1011*1*0**010\) 如何进行还原？

使用枚举的方法，四个位置未知，每个位置有两种情况，因此，共 \(2^4=16\) 种情况。

成本分析

MA.Hashing 可以处理多种不同的查询，一个有 n 个属性的关系有 \(2^n\) 种不同的查询，而这些不同的查询就会有不同的代价：\(Cost(Q)=2^s\)，这里的 \(s=\sum_{i\notin Q}d_i\)。

查询分布可以大大帮助我们提升查询效率，所谓的查询分布会给出提出每种查询的概率 \(P_Q\)。可以用一个例子来看，假设对于某个关系有以下几种查询：

select * from R where a=1;
select * from R where d=2;
select * from R where b=3 and c=4;
select * from R where a=5 and b=6 and c=7;

其中第一种比较常见，而第三种比较少见，那么在复合哈希值中就可以给属性 a 更多的比特位，而后两种更少的比特位。现在来看具体的代价：

• 如果所有的属性值都已知，那么 \(MinCost_{pmr}=1\)
• 如果所有的属性值都未知，那么 \(MaxCost_{pmr}=2^d=b\)
• 平均代价为所有查询类型的加权求和，\(AvgCost_{pmr}=\sum_{P_Q}\prod_{i\notin Q}2^{d_i}\)

除了上述的查询分布，还有其他方法来优化多属性查询效率：

• Attribute Domain 的规模，比如一个属性的取值只有 4 个，那么就不会给他安排多于 2 个 bits
• Discriminatory Power，如果某个属性比其他属性更具辨识度，即取值更加不重复，那么就给他分配更多的 bits