数据库内核：PostgreSQL 关系操作与评估2

选择（Selection）

选择：select * from R where C，从一个关系 R 中过滤元组，得到符合条件 C 的子集。

选择操作根据选择条件可以分为三大类：

• 1-d：一维的，也就是选择条件只基于一个属性
• n-d：多维的，也就是选择条件基于多个属性
• similarity：近似匹配或者带有排序的

假设 \(r_q\) 为 匹配查询 q 的元组的数量，\(b_q\) 为包含匹配查询 q 的元组的页面的数量。选择有多种不同的策略：

• One Type Query：返回的结果至多只有一个，即 \(r_q = b_q = 1\)。例如 select * from R where id = 1234;。
• Partial Match Retrieve：基于单个或多个条件返回多个结果元组，即 \(0 \leq r_q \leq r, 0 \leq b_q \leq b+b_{ov}\)。例如 select * from R where age=65; (1-d) 和 select * from R where age=65 and gender=’m’; (n-d)。
• Range Queries：此时不再基于等性测试条件，而是基于范围，即 \(0 \leq r_q \leq r, 0 \leq b_q \leq b+b_{ov}\)。例如 select * from R where age&geq18 and age&leq21; (1-d) 和 select * from R where age between 18 and 21 and height between 160 and 190; (n-d)。
• Pattern-based Queries：基于模式的匹配，即 \(0 \leq r_q \leq r, 0 \leq b_q \leq b+b_{ov}\)。例如 select * from R where name like '%oo%';。

为了更有效率地进行选择，有几种比较基本的方法：

• 对元组进行排序 (Sorting) 或者哈希 (Hashing)
• 使用额外的索引结果，比如 Index Files、Signature

Heap Files

选择

在 Heap Files 中的选择，只有一种策略，就是通过线性扫描文件搜索匹配的元组：

// select * from R where C
for each page P in file of relation R {
    for each tuple t in page P {
        if (t satisfies C)
         	 add tuple t to result set
		} 
}

在 Heap Files 中的选择，需要从第一个页面扫描到最后一个页面：

成本分析：\(Cost_{range}=Cost_{pmr}=b\)

如果我们知道只有一个元组与查询匹配（一个查询），那么就可以在找到一个查询之后就不用继续扫描了。此时的成本为 \(Cost_{one}: best=1, average=\frac{b}{2},worst=b\)。

插入

只需要将新元组插入到文件最后一个页面，伪代码如下：

rel = openRelation(”R”, READ|WRITE); 
pid = nPages(rel)-1;
get_page(rel, pid, buf);
if (size(newTup) > size(buf))	// 检查新元组的大小是否超过缓冲区的大小
   { deal with oversize tuple }
else {
   if (!hasSpace(buf,newTup))	// 检查缓冲区是否有足够的空间来容纳新元组
      { pid++; nPages(rel)++; clear(buf); }
   insert_record(buf,newTup);
   put_page(rel, pid, buf);
}

成本分析：\(Cost_{insert}=1_r+1_w\)，如果加入的元组很大，则可能需要额外的写入，例如 PostgreSQL 的 TOAST。

其他策略：从R中找到任何有足够空间的页面，最好是已经加载到内存缓冲区的页面（而不一定非要是最后一页）。

PostgreSQL 中的策略：使用在缓冲池中最后一个被更新 (MRU) 的关系 R 的页。如果条件不满足，在缓冲池中寻找一个有足够空间的页，使用 FSM (Free Space Map) 来寻找这样一个满足条件的页，具体见 backend/access/heap/{heapam.c,hio.c}。

在 PostgreSQL 中的元组插入：

• heap_insert(Relation relation, HeapTuple newtup, CommandId cid, ...)
• 找到有足够的可用空间用于新元组的页面
• 确保页面加载到缓冲池并锁定
• 将元组数据复制到页面缓冲区，设置 xmin 等
• 将缓冲区标记为脏
• 将插入的详细信息写入事务日志
• 如果关系有 OID，则返回新元组的 OID

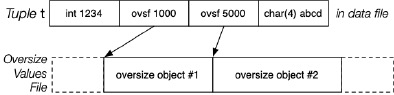
对于大元组的插入，这个时候我们需要一个独立于数据文件的额外文件（比如 PostgreSQL 的 Toasting）。比如在下图中，元组 t 的第二个属性的值无法存放在元组中，因此，我们会将该属性的值存放在一个额外的文件中，而在元组中的对应位置留下一个标记 (Marker) ，这个标记会告诉系统该属性值存放在额外文件中的哪个位置。

for i in 1 .. nAttr(t) {
	if (t[i] not oversized) continue
	off = appendToFile(ovf, t[i])
	t[i] = (OVERSIZE, off)
}
insert into buf as before

删除

伪代码：

rel = openRelation(”R”,READ|WRITE); 
for (p = 0; p < nPages(rel); p++) {
    get_page(rel, p, buf);
    ndels = 0;
    for (i = 0; i < nTuples(buf); i++) {
        tup = get_record(buf,i);
        if (tup satisfies Condition)
                    { ndels++; delete_record(buf,i); }
        }
    if (ndels > 0) put_page(rel, p, buf); 
  	if (ndels > 0 && unique) break;
}

在 PostgreSQL 中的元组删除：

• heap_delete(Relation relation, ItemPointer tid, ..., CommandId cid, ...)
• 将包含元组的页面放入缓冲池并锁定它
• 在元组中设置标志、命令 ID 和 xmax，标记为脏缓冲区
• 向事务日志写入删除指示

Vacuuming 最终会压缩每页的空间。

更新

对更新的分析类似于删除：需要遍历所有页面，替换每一个需要更新的元组（在每页内），将有修改的页面写回磁盘。

成本分析：\(Cost_{update}=b_r+b_{w}\)

注意：如果更新后的元组大小不再合适原有的页面，此时就需要先去重新排布页中的空闲空间，以求能有充足的空间来放置修改后的元组。

在 PostgreSQL 中的元组删除：

• heap_update(Relation relation, ItemPointer otid, HeapTuple newtup, ..., CommandId cid, ...)
• 本质上就是先进行 Deletion，再进行 Insertion
• 设置旧元组的 ctid 字段以引用新元组
• 如果没有引用交易，也可以就地更新

在 PostgreSQL 中的实现

默认情况下，PostgreSQL 将所有的关系（还有索引文件）都以 Heap File 进行存储。如果有需要使用其他形式（比如 Sorted, Hashed）的文件，PostgreSQL 可以生成一个符合形式的副本，可以使用关键字 create index...using hash，Heap file 在 PostgreSQL 中的实现在 src/backend/access/heap。

PostgreSQL 中的 Heap file 可能会使用多个物理文件，文件以相应表的 OID 命名，第一个数据文件简称为 OID，如果大小超过 1GB，就会创建一个名为 OID.1 的 fork，随着数据大小的增长添加更多 fork（每1GB一个 fork）。除了数据文件，还有 free space map（空闲空间映射，OID_fsm）、visibility map（OID_vm），另外如果有元组的属性非常大就还有 TOAST 文件。

Sorted Files

记录按某个字段 k（排序键）的顺序在文件中进行存储。这将是查找的效率提高，但是插入的效率降低。因此，为了缓解插入的成本，会使用溢出页面。

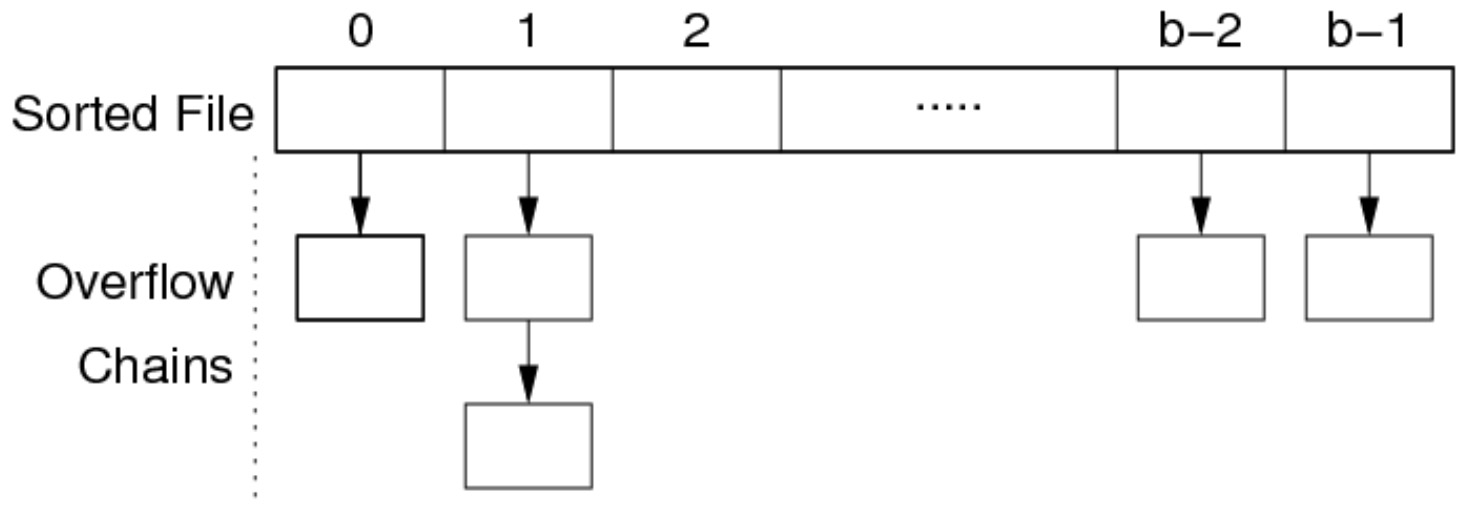
当某个页面满了之后，直接为该页面创建一个溢出页面，而不是将之后的元组顺延。假设溢出页面的总数为 \(b_{ov}\)，那么溢出链表的平均长度为 \(\frac{b_{ov}}{b}\)。我们称一个页面和它的溢出链表为一个 Bucket。

选择

如果查询结果只有一个，并且文件是按顺序存储的，因此查询可以使用二分查找。

// select * from R where k = val  (sorted on R.k)
// rel 表示 Relation
// mid, lo, hi 表示 Page Index
// k 表示条件属性 (The Sort Key)
// val, loval, hival 表示 k 的值
lo = 0; hi = b - 1; 
while (lo <= hi) {
    mid = (lo + hi) / 2;
    (tup, loVal, hiVal) = searchBucket(f, mid, x, val);
    if (tup != NULL) return tup;
    elseif(val < loVal) hi = mid - 1;
    elseif(val > hiVal) lo = mid + 1;
    else return NOT_FOUND;
}
return NOT_FOUND;

这里的二分法搜索先是以页面为单位的，首先找到 Middle Page，在该页面的 Bucket 中寻找有无目标元组，searchBucket() 就是进行该任务的，如果能知道满足条件的元组就直接返回，否则返回 NULL，同时还会返回该 Bucket 中，最小和最大的 Key Value，如果没有找到目标元组，则需要这两个值来向前或者向后进行后续的搜索。

searchBucket(f,p,k,val) {
    buf = getPage(f,p);	// 获取第 p 个页面
    (tup,min,max) = searchPage(buf,k,val,+INF,-INF) // 搜索这个页面，如果找到 k 的元组，则返回该元组，否则返回NULL，另外还要返回这个页面的最大、小值
    if (tup != NULL) return(tup,min,max);	// 如果找到元组就返回
    ovf = openOvFile(f);	// 没找到，就继续在溢出页面中搜索，先获取溢出文件的句柄
    ovp = ovflow(buf);	// 获取当前页面 buf 中的溢出页面号
		while (tup == NULL && ovp != NO_PAGE) {
        buf = getPage(ovf,ovp);
        (tup,min,max) = searchPage(buf,k,val,min,max) 
        ovp = ovflow(buf);
    }
    return (tup,min,max);
}

// 在给定页面 buf 中根据键 k 和值 val 进行搜索，并返回满足条件的元组以及键的最小值和最大值
searchPage(buf,k,val,min,max) {
    res = NULL;
    for (i = 0; i < nTuples(buf); i++) {
    		tup = getTuple(buf,i);
    		if (tup.k == val) res = tup; 
      	if (tup.k < min) min = tup.k; 
      	if (tup.k > max) max = tup.k;
    }
    return (res,min,max);
}

成本分析：上述方法都将每个桶视为一个大的页面。因此，最好的情况就是在第一个页面就找到了匹配的元组 \(Cost_{one}=1\)，最差情况就是执行完二分查找，最终还是没有找到想要的元组 \(Cost_{one}=log_2b+b_{ov}\)。平均情况需要根据数据的分布来确定，其成本 \(Cost_{one}=b_{examine}+b_{ov}\)。

练习：数据分布如下，\(b=5,c=4\)：

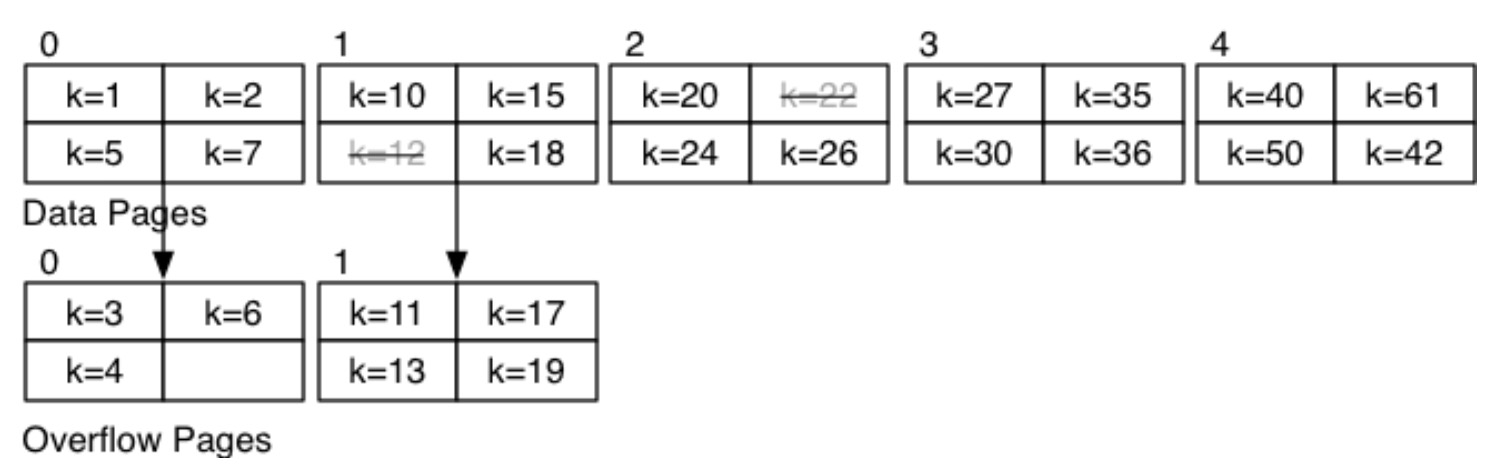
计算以下查询的成本：

• select * from R where k = 24;：首先搜索索引为 2 的页面，发现存在键为 24 的元组。因此，成本 \(Cost=1\)。
• select * from R where k = 3;：首先搜索索引为 2 的页面，未发现键为 3 的元组。而该页面最小值也大于 3。所以接下来检索索引为 0 的页面，在该页面未找到键为 3 的元组，但是存在溢出页面，所以加载溢出页面继续检索，在第一个溢出页面找到元组。因此，成本 \(Cost=3\)。
• select * from R where k = 14;：首先搜索索引为 2 的页面，未发现键为 3 的元组。接下来检索索引为 0 的页面，在该页面未找到键为 3 的元组。检索索引为 0 的溢出页面，也未找到。最后，检索索引为 1 的页面和其溢出页面，均为找到。二分查找终止，其成本 \(Cost=5\)。
• select max(k) from R;：因为数据是按照顺序来存储的，因此最大值在最后一页，所以直接检索最后一页，由于没有溢出页面，所以其成本 \(Cost=1\)。

对于 Partial Match Retrieve ，由于目标属性 k 的取值会有重复，因此有可能具备相同值的元组分布在多个不同的页面中，如 select * from R where k = 2;：

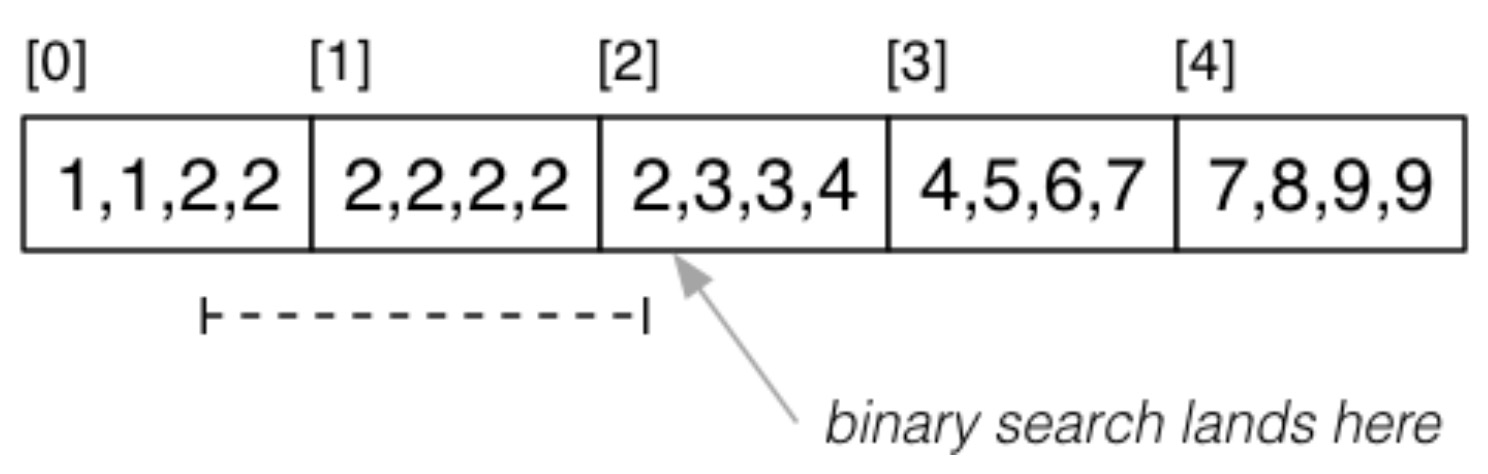
此时当我们使用二分法查找时，会首先找到索引为 2 的页面，但索引为 1、3 的页面都有可能包含符合条件的元组。此时代价为 \(Cost_{pmr}=Cost_{one}+(b_q-1)\cdot(1+b_{ov})\)。

对于 Range Query ，首先来看目标属性 k 的取值不会有重复时的情况，如 select * from R where k >= 5 and k <= 13;：

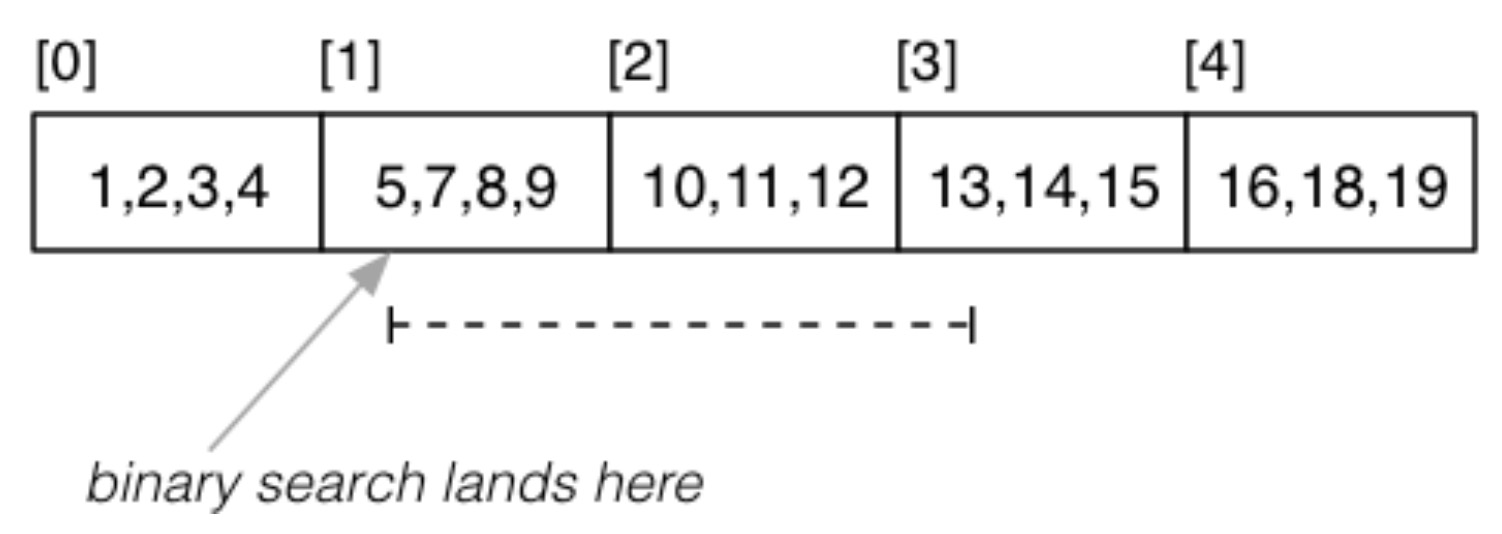
首先用二分查找的方式找到下界，然后按照顺序遍历直到上界。因此其成本为 \(Cost_{range}=Cost_{one}+(b_q-1)\cdot(1+b_{ov})\)。

另外一种情况就是目标属性 k 的取值存在重复的情况，如 select * from R where k >= 2 and k <= 6：

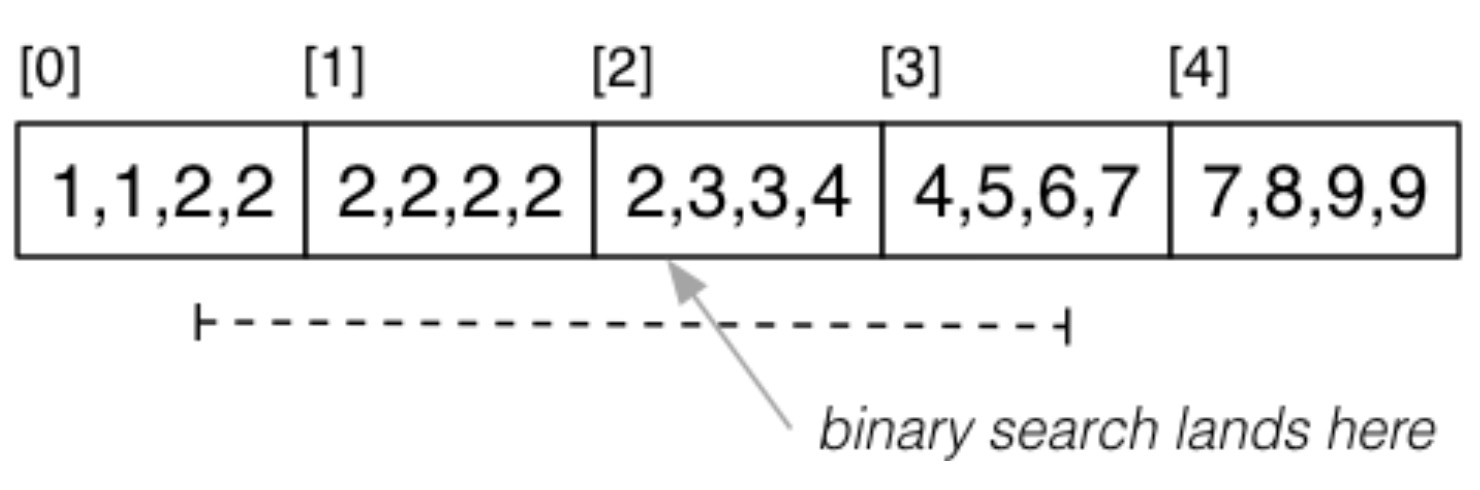
首先用二分查找的方式找到下界，因为有重复的情况，所以需要继续向前搜索，找到真正的“下界”，即第一个下界元组所在的页面，然后开始向后查找，直到找到上界。因此其成本为 \(Cost_{range}=Cost_{one}+(b_q-1)\cdot(1+b_{ov})\)。

以上考虑的所有情况都是在属性 k 为排序键的情况，那么，如果条件属性不是排序键的话，此时检索的方式就跟 heap files 相同。

插入

思路：通过二分查找的方式找到适合插入的页面， 如果该页面没有满，就直接插入，如果满了，就插入到溢出页面。因此其成本为 \(Cost_{insert}=Cost_{one}+\delta_w\)，这里的 \(\delta_w\) 要么为 1 要么为 2。

练习：当数据分布如下时：

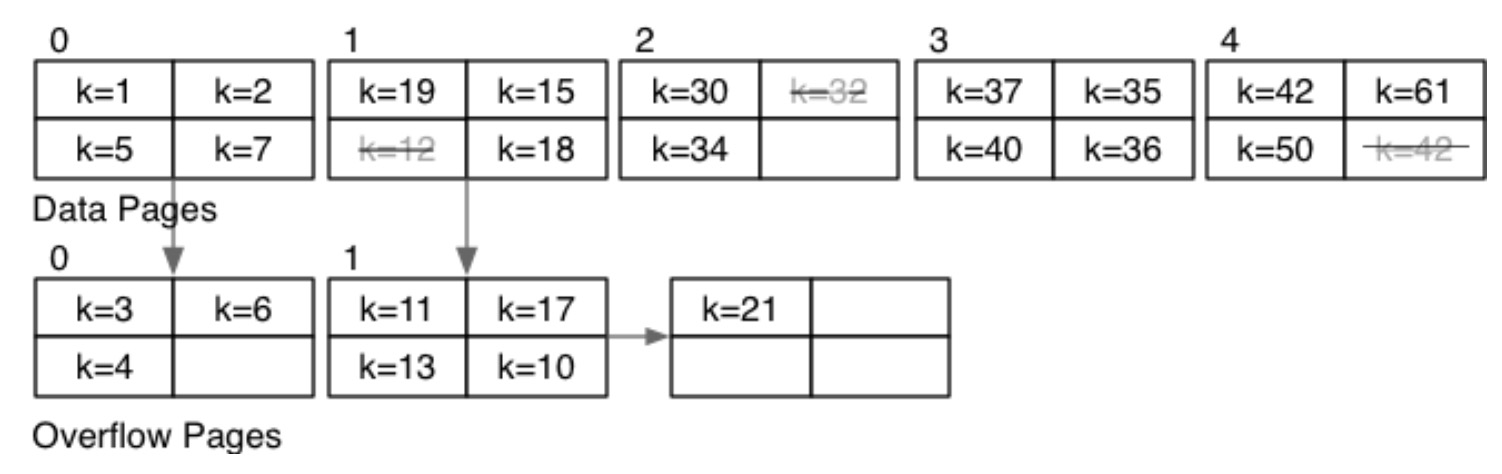
• 插入 \(k=33\)：根据二分查找，首先检索索引为 2 的页面，该页面最大值为 34，最小值为 30，因此插入到这个页面，由于有空闲位置，所以其成本为 \(Cost_{insert}=Cost_{one}+\delta_w=1+1=2\)。
• 插入 \(k=25\)：根据二分查找，首先检索索引为 2 的页面，其最小值大于 25，接着找索引为 0 的页面，以及其溢出页面，最大值都小于 25。接着检索索引为 1 的页面，以及其溢出页面，最大值都小于 25，但是已经二分查找完了，因此 25 插入到索引为 1 的页面中。因此其成本为 \(Cost_{insert}=Cost_{one}+\delta_w=6+1=7\)。
• 插入 \(k=99\)：根据二分查找，首先检索索引为 2 的页面，其最大值小于 99。接着遍历索引为 3 的页面，其最大值小于 99。再接着遍历索引为 4 的页面，其最大值小于 99，但是由于最后一页了，所以就插入到该页面。因为该页面满了，所以其成本为 \(Cost_{insert}=Cost_{one}+\delta_w=3+2=5\)。

删除

基本操作依旧与选择一样，先找到对应的页面，然后找到对应的元组，将其标记为 Deleted。它的代价同样和 \(b_q\) 相关，如果 k 取值没有重复，则 \(b_q = 1\)，如果有重复，\(b_q > 1\)。

其代价为 \(Cost_{delete}=Cost_{select}+b_{qw}\)。

Hashed Files

简介

基本思想：使用键的哈希值来计算元组的页面地址。

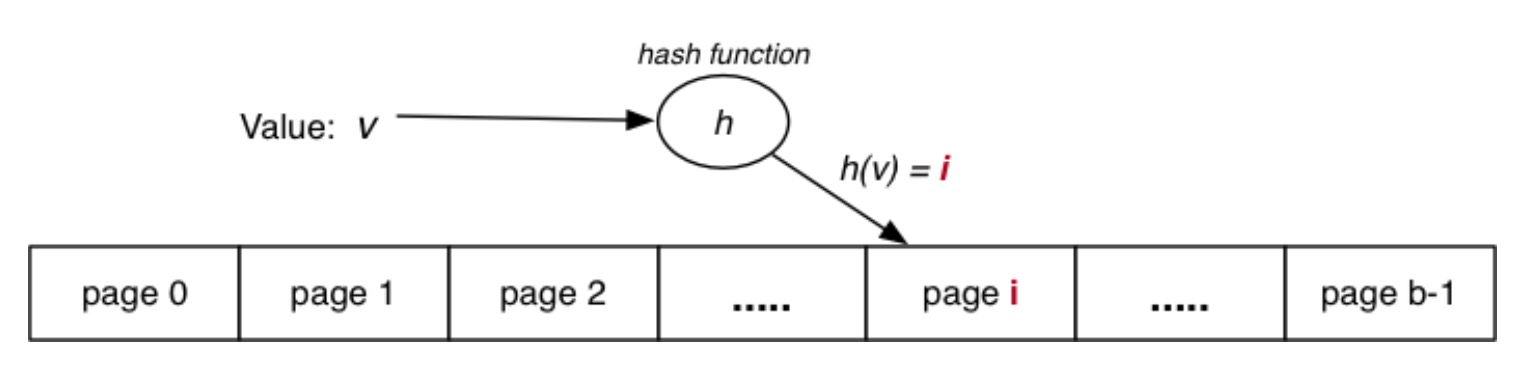
因此，哈希函数需要能将键值的范围映射到 \([0,b-1]\) 中。哈希函数函数将键值（任何类型）转换为整数值，该值与页面的索引相对应，可以将整数值视为位字符串。

在 PostgreSQL 中的哈希函数如下，可以将任意一种类型的值映射为一个 32 bit 的整数值：

// backend/access/hash/hashfunc.c
Datum hash_any(unsigned char *k, register int keylen) {
   register uint32 a, b, c, len;
   /* Set up the internal state */
   len = keylen;  a = b = c = 0x9e3779b9 + len + 3923095;
   /* handle most of the key */
   while (len >= 12) {
       a += ka[0]; b += ka[1]; 
     	 c += ka[2]; mix(a, b, c);
       ka += 3; len -= 12;
   }
   /* collect any data from last 11 bytes into a,b,c */
	 mix(a, b, c);
   return UInt32GetDatum(c);
}

有两种方法将 hash_any 函数计算得到的原始哈希值转换为页面的地址。

• 如果 \(b=2^k\)，进行 “位与” 操作

uint32 hashToPageNum(uint32 hval) { 
  	uint32 mask = 0xFFFFFFFF;
		return (hval & (mask >> (32-k)));
}

• 否则，使用取余操作

uint32 hashToPageNum(uint32 hval) {
    return (hval % b);
}

这么做有两个目的。第一，可以将元组均匀地分布在各个哈希桶中；第二，会使得每个哈希同尽可能存满，不浪费空间。所以此时：

• 最好的情况：每个哈希桶有几乎数量一致的元组
• 最坏的情况：所有的元组都被映射到同一个哈希桶中
• 通常情况：一部分哈希桶有着更多的元组

使用溢出页面处理“超满”桶，每个桶中的所有元组必须具有相同的哈希值。

性能

对于 Hashed Files，有两个重要的评估指标：

• 负载因子（load factor）：\(L=\frac{r}{bc}\)，\(r\) 是元组的总数；\(b\) 是页面的总数；\(c\) 是每个页面的容量。所以 \(bc\) 就是理论最多能容纳的元组的数量。我们用 \(L\) 来表示每个页面被填充的程度，最理想的就是 \(r = bc\)，即 \(L=1\)，此时存储的元组刚好为理论最大，每个页面存储的元组数量相同。
• 平均溢出页面长度：\(Ov=\frac{b_{ov}}{b}\)

根据元组在 Hashed Files 中的分布，分为三种情况：

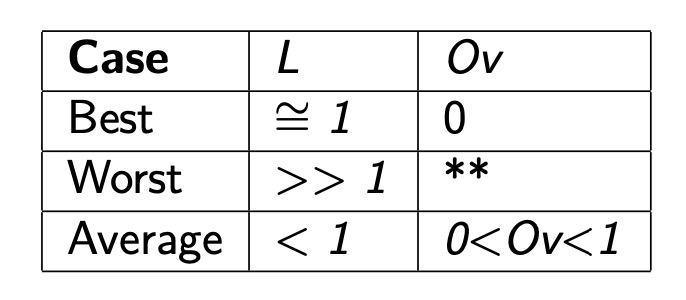
这里的 \(**\) 表示与 Heap Files 性能一样。通常情况下，我们期望保持 \(0.75 < L < 0.9\)。

选择

首先来看 One Type Query：只需要对键值使用哈希函数，得到目标页面 P，接着在该页面及其溢出页面中搜索即可，其伪代码如下：

// select * from R where k = val
pid,P = getPageViaHash(val,R)
for each tuple t in page P {
    if (t.k == val) return t
}
for each overflow page Q of P {
    for each tuple t in page Q {
        if (t.k == val) return t
		}
}

成本分析：

• 最好情况：\(Cost_{one}=1\)
• 最坏情况：\(Cost_{one}=1+max(Ovlen)\)
• 平均情况：\(Cost_{one}=1+\frac{Ov}{2}\)

再看 Partial Match Retrieve：因为结果不唯一，所以要找到所有的结果，其伪代码如下：

// select * from R where nk = val
pid,P = getPageViaHash(val,R)
for each tuple t in page P {
    if (t.nk == val) add t to results
}
for each overflow page Q of P {
    for each tuple t in page Q {
        if (t.nk == val) add t to results
    }
}
return results

其成本为 \(Cost_{pmr}=1+Ov\)。

最后看 Range Query：因为 Hash Files 是完全无序的，所以需要扫描所有的页面去找到符合条件的元组。其成本为 \(Cost_{range}=b+b_{ov}\)。而对于那些不是键的属性的搜索，则和 Heap Files 完全一样，其成本为 \(Cost_{one}=Cost_{pmr}=Cost_{range}=b+b_{ov}\)。

插入

插入操作则与 One Type Query 差不多，其伪代码如下：

// insert tuple t with key=val into rel R
pid,P = getPageViaHash(val,R)
if room in page P {
    insert t into P; return
}
for each overflow page Q of P {
    if room in page Q {
        insert t into Q; return
		}
}
add new overflow page Q 
link Q to previous page 
insert t into Q

成本分析：

• 最好的情况：找到的页面有足够的空间用于插入，其成本为 \(Cost_{insert}=1_r+1_w\)。
• 最坏的情况：寻遍该页面的所有溢出页面没有足够的空间，因此需要再创建一个新的溢出页面，其成本为 \(Cost_{insert}=1_r+max(Ovlen)_r+2_w\)。

练习：一个 Hashed files，其 \(b=4,c=3,d=2,h(x)=bits(d,hash(x))\)。使用以下键的哈希值按照字母顺序插入 Hashed files 中，哈希值是完整 32位 哈希中的 5 个低位。

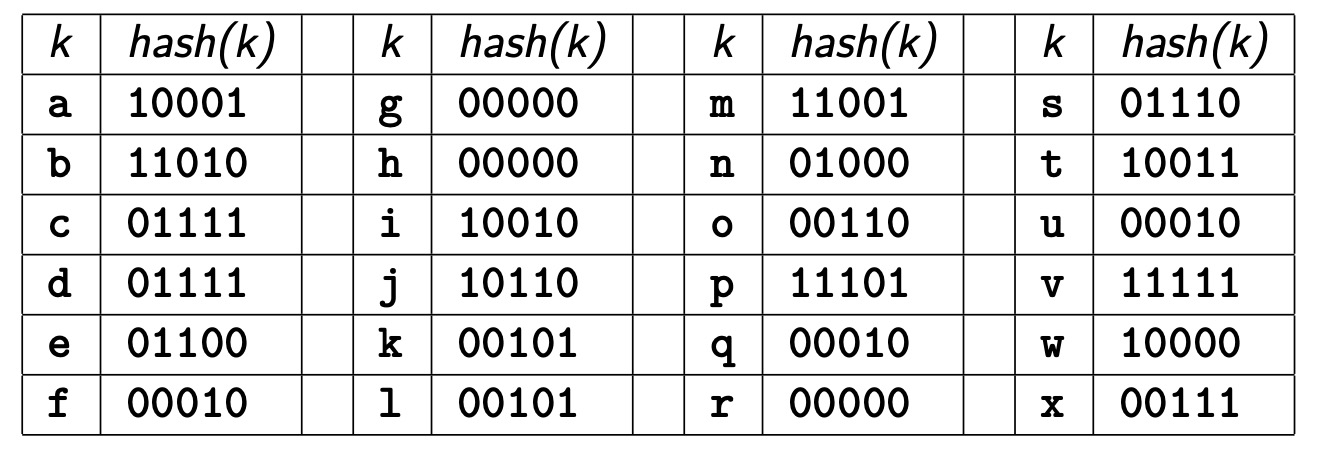
页面 0：e	g	h	n			溢出页面 0：r	w

页面 1：a	k	l	m			溢出页面 0：p

页面 2：b	f	i	j			溢出页面 0：o	s	u

页面 3：c	d	t	v			溢出页面 0：x

删除

删除与与目标属性取值有重复的查询类似，区别仅在与最后要将修改过的页面写回磁盘：

// delete from R where k = val; 
pid,P = getPageViaHash(val,R)	// 根据val的哈希值找到存储该值的数据页的页号pid和页P
ndel = delTuples(P,k,val)	// 删除页P中满足条件k=val的记录
if (ndel > 0) putPage(f,P,pid)	// 有需要删除的元组，将修改后的页P写回数据文件f中的对应页号
for each overflow page qid,Q of P {	// 处理溢出页面
    ndel = delTuples(Q,k,val)
		if (ndel > 0) putPage(ovf,Q,qid) 
}

哈希的问题

到目前为止，对哈希的讨论都是在固定的文件大小的前提下进行的。因此哈希的性能会随着溢出页面的增加而降低。当然，我们可以将文件的固定大小设置的非常大，这样就可以避免溢出页面增长速度过快的问题，但是大量的空闲页面会造成浪费。

所以，为了克服上面的问题，文件的大小就不能固定。而大小不固定就需要一个不固定的哈希函数，有两种方法：

• 可扩展哈希，动态哈希 (Extendible hashing, Dynamic hashing)：这种方法需要 Directory，且 Directory 会随着文件尺寸的增长不断增长，但是不需要溢出页面。
• 线性哈希 (Linear Hashing)：系统性地扩展文件，不需要 Directory，但是需要溢出页面。该方法更加推荐。

所有可变哈希方法，都将哈希值作为一个 32 位的位字符串。哈希函数发生变化时，实际上就是使用更多或者更少的位字符串。

首先使用哈希函数将数值转换为一个 32 位的位字符串：uint32 hash(unsigned char *val)

然后，使用一个函数从其中提取 d 位的子串： unit32 bits(int d, uint32 val)

使用这个子串来表示页面的地址。

练习：位操作

写一个函数将 uint32 的值显示为二进制字符串表示。

char *showBits(uint32 val, char *buf) {
    uint32 mask = 1 << (sizeof(uint32) * 8 - 1);  // // 从最左边的位开始，将1左移动31位，，mask就是10000000000000000000000000000000
    // 遍历每一位
    for (int i = 0; i < sizeof(uint32) * 8; i++) {
        if (val & mask) {	// 将val和mask进行与操作，只有当两个位都为1时，结果位才为1
            *buf = '1';  // 将缓冲区中对应的位设为'1'
        } else {
            *buf = '0';  // 将缓冲区中对应的位设为'0'
        }
        buf++;	// 移动到缓冲区中的下一个字符
        mask >>= 1;	// 将掩码向右移动1位
    }
    *buf = '\0';	// 在缓冲区末尾添加空字符，表示字符串的结束
    return buf;
}

写一个函数来提取一个 uint32 值的 d 位，如果 d > 0，提取低位的 d 位；如果 d < 0，提取高位的 d 位。

uint32 bits(int d, uint32 val) {
    if (d > 0) {	// 提取低位
        uint32 mask = (1 << d) - 1;	// 将1左移d位并减去1得到一个最右边d位为1其余为0的32位数
        return val & mask;
    } else if (d < 0) {	// 提取高位
        int numBits = sizeof(uint32) * 8;
        uint32 mask = ((1 << (-d)) - 1) << (numBits - (-d));	// 得到左边d位为1其余为0的32位数
        return (val & mask) >> (numBits - (-d));
    } else {
        return 0;
    }
}

分割

可变哈希的一个重要的概念就是“分割”。因为同一个页面的所有元组的哈希值都相同，因此可以通过考虑额外的位来重新计算元组的页地址。比如，当前的页面是 101，那么新的页面的哈希值就可以是 0101 和 1101。然后原来在 101 页面的元组一部份保留，101 页面也就是 0101，另一部份移动到新的页面 1101 中。也要对 101 这个页面的溢出页面进行相同的操作。

结果：可扩展的数据文件，就不需要全部推倒进行重建了，只需要对部份页面进行修改就可以实现扩展的功能。

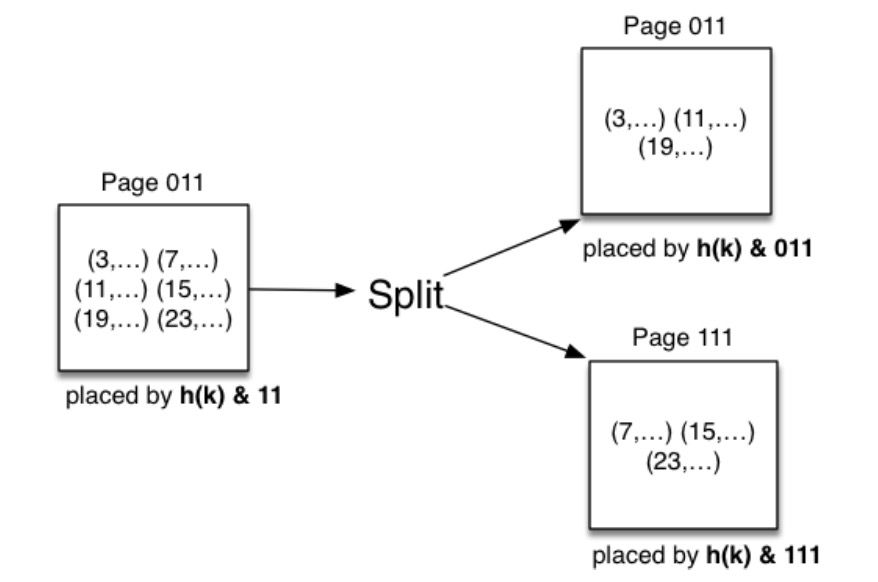
线性哈希（Linear Hashing）

文件的组织

• 主要数据块的文件
• 溢出数据块的文件
• 用于存储分割的指针（sp）的寄存器

使用系统的方法来增长数据文件，哈希函数需要“适应”地址范围的变化，系统的分割来控制溢出页面的长度。优点就是不需要目录的辅助存储，而缺点则是需要溢出页面。

线性哈希

文件线性增长（每一次扩充只增加一个块，定期增长）。线性哈希中的文件扩展分为以下几个阶段：

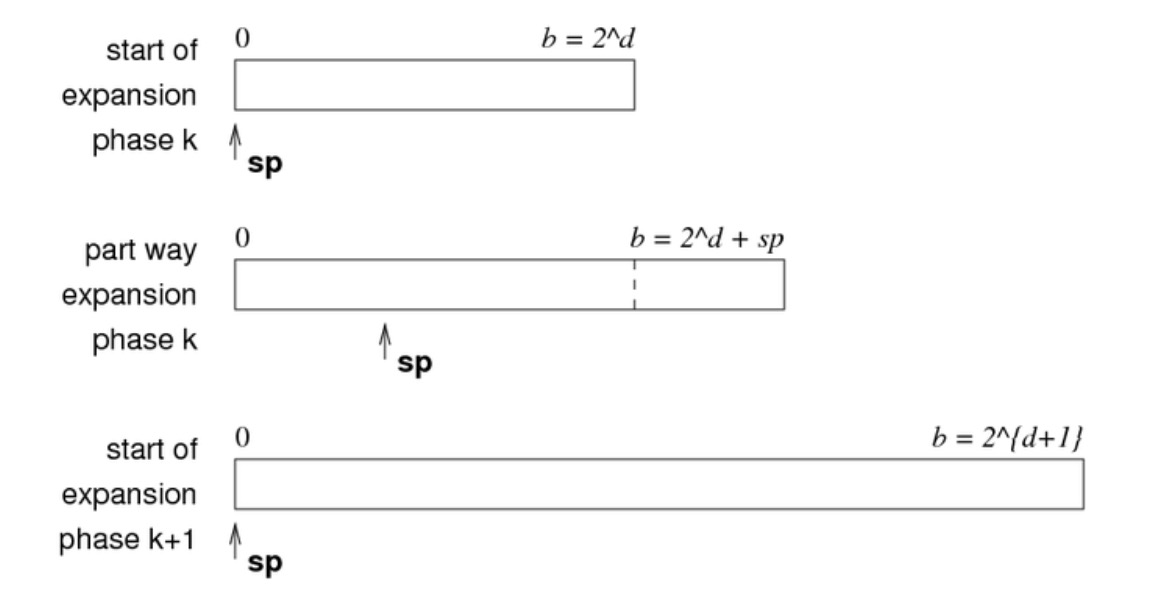
• 在最初的阶段，只有原文件，此时共有 \(b=2^d\) 个页面
• 当不断添加页面时，sp 会不断增大，增大的具体数值等于新加入的页面数量
• 当 \(sp = 2^d\) 时，此时整个文件的尺寸翻倍，就需要将 sp 重新置于开头

选择

如果 \(b=2^d\)，该文件的行为与标准哈希完全相同，使用 d 位哈希来计算页面地址。

// select * from R where k = val;
h = hash(val);
P = bits(d,h);  // 取d位
for each tuple t in page P and its overflow pages {
    if (t.k == val) return t;
}

成本分析：\(Cost_{average}=1+Ov\)。

如果 \(b!=2^d\)，此时 sp 一定不会在整个文件的开头，因此需要用不同的方式来对待文件的不同部分。

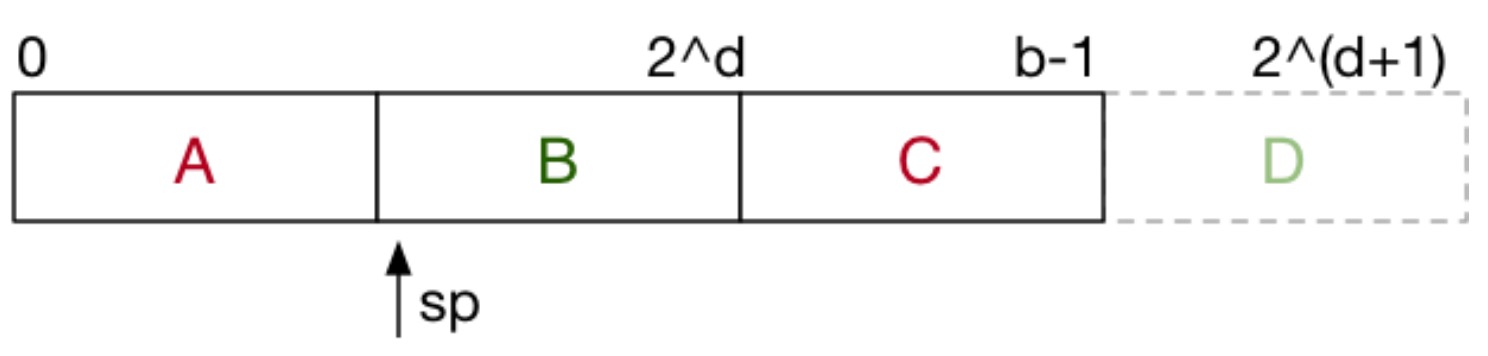
此时的 Part A 和 Part C 被当做一个规模为 \(2^{d+1}\) 的文件部分（Part A 和 Part C 的地址哈希值只差了一位，比如一个是 0101，一个是 1101）。Part B 被当做一个规模为 \(2^d\) 的文件部分。也就是说，如果通过哈希函数得到的地址哈希值小于 sp，那么，就需要地址哈希值需要多取一位才行，这样才能确认该元组是在 Part A 还是 Part C 之中。而 Part B 是跟该元组不关联的页面，因此可以直接根据地址哈希来判断元组是否在其中。Part D 目前还不存在，但随着不断增加页面，直到整体规模为 \(2^k\) 时，Part D 就形成了。

因此，调整后的搜索算法如下：

// select * from R where k = val
h = hash(val);
p = bits(d,h);
if (P < sp) { p = bits(d+1,h); } // 多取一位
P = getPage(f, p)
for each tuple t in page P and its overflow blocks {
    if (t.k == val) return R;
}

以下是线性哈希对文件尺寸进行扩展的例子：

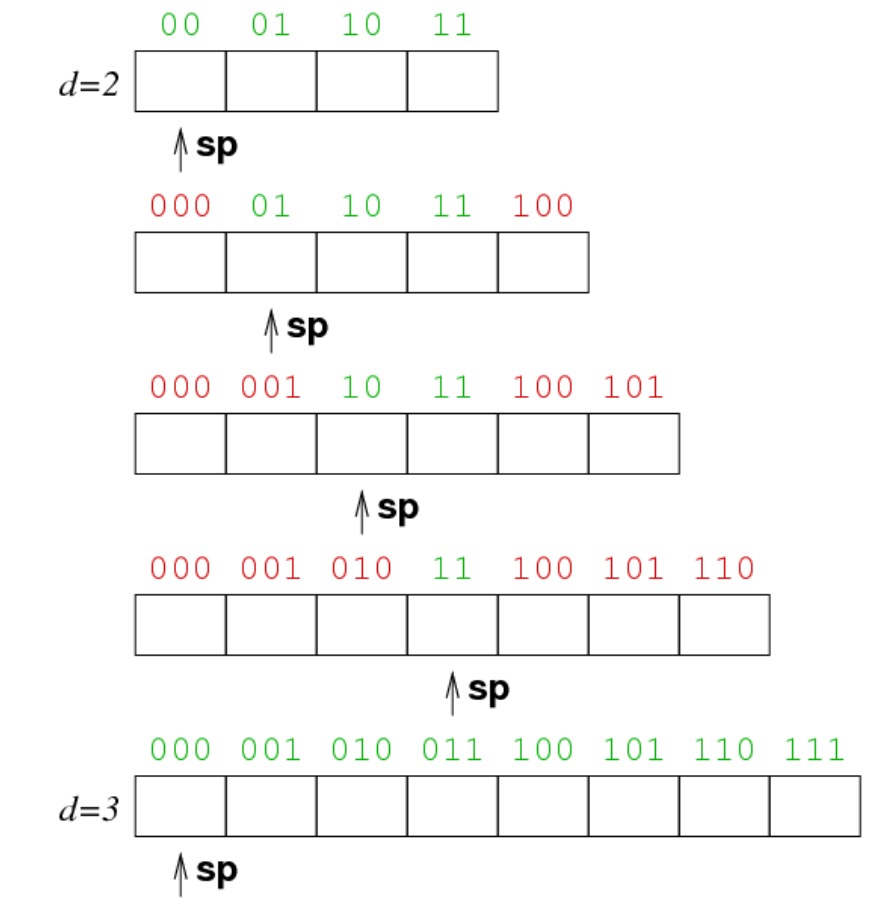
插入

插入操作和一般的 Hash File 一样，只是需要多检查一位哈希值，同时，还需要进行分割，其伪代码如下：

p = bits(d,hash(val));
if (p < sp) P = bits(d+1,hash(val));
// bucket P = page P + its overflow pages P = getPage(f,p)
for each page Q in bucket P {
		if (space in Q) { 
      	insert tuple into Q 
        break
		} 
}
if (no insertion) {
		add new ovflow page to bucket P 
    insert tuple into new page
}
if (need to split) {
		partition tuples from bucket sp into buckets sp and sp+2^d
		sp++;
		if (sp == 2^d) { d++; sp = 0; } 
}

成本分析：

如果不需要分割，成本与标准哈希相同。

此时成本为 \(Cost_{best}=1_r+1_w,Cost_{average}=(1+Ov)_r+1_w,Cost_{worst}=(1+max(Ov))_r+2_w\)。

如果发生了分割，插入成本还需要加上分割的成本：

• 读取 sp 所指的页面（包括其溢出页面）
• 写 sp 所指的页面（包括其新产生的溢出页面）
• 写 \(sp+2^d\) 所指的页面（包括其新产生的溢出页面）

因此，平均来讲，分割的成本为 \(Cost_{split}=(1+Ov)_r+(2+Ov)_w\)

分割

有两种方式来触发分割：

• 每当有一个元组插入到一个已满的页面时
• 当负载因子达到一定的阈值时，比如每进行 k 次插入时

注意：分割总是发生在 sp 当前指向的页面，即使该页面未满或者当前插入的页面不是 sp 所指的页面。

分割可以减少每个溢出页面的长度，有助于保持短的平均溢出页面长度。

以下是分割的图示：

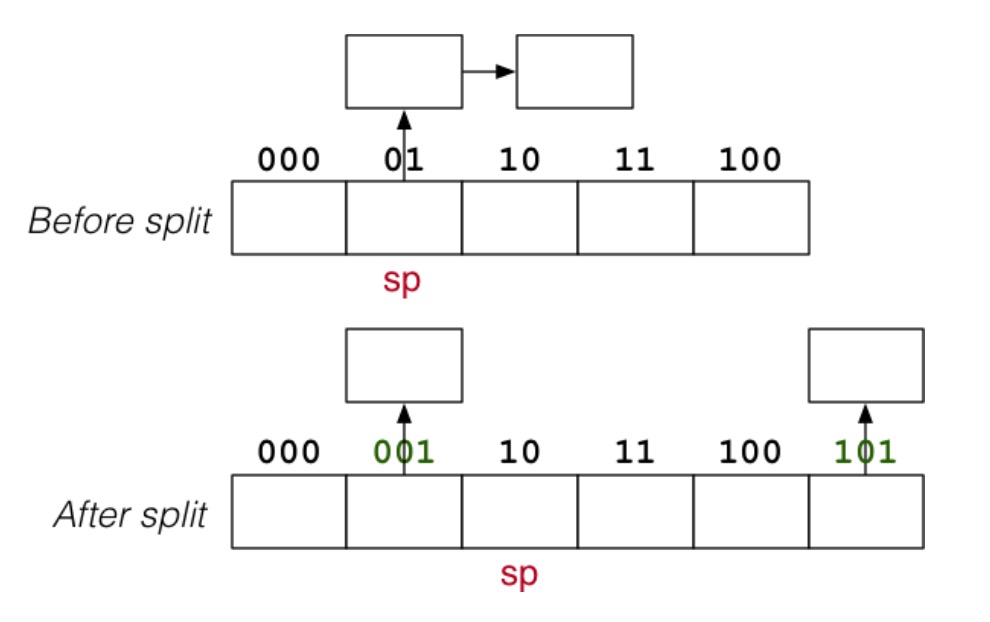
以下是分割的算法：

// partition tuples between two buckets
newp = sp + 2^d; oldp = sp;
for all tuples t in P[oldp] and its overflows {
    p = bits(d+1,hash(t.k));
    if (p == newp)
        add tuple t to bucket[newp]
    else
        add tuple t to bucket[oldp]
}
sp++;
if (sp == 2^d) { d++; sp = 0; }

删除

删除操作和一般静态哈希文件一样。但是，当删除足够的元组时，需要压缩文件。因为当 r 缩小后，而 b 依旧很大，这就浪费了空间。 此时需要进行 Splitting 的反操作，将最后一个哈希桶移除，将这个哈希桶中的元组和其相关哈希桶中的元组进行合并，放入后一个未删除的哈希桶中。

练习

将下面元组按照字母的顺序插入到哈希文件中，哈希文件的 \(b=4,c=3,d=2,sp=0,h(x)=bits(d,hash(x))\)

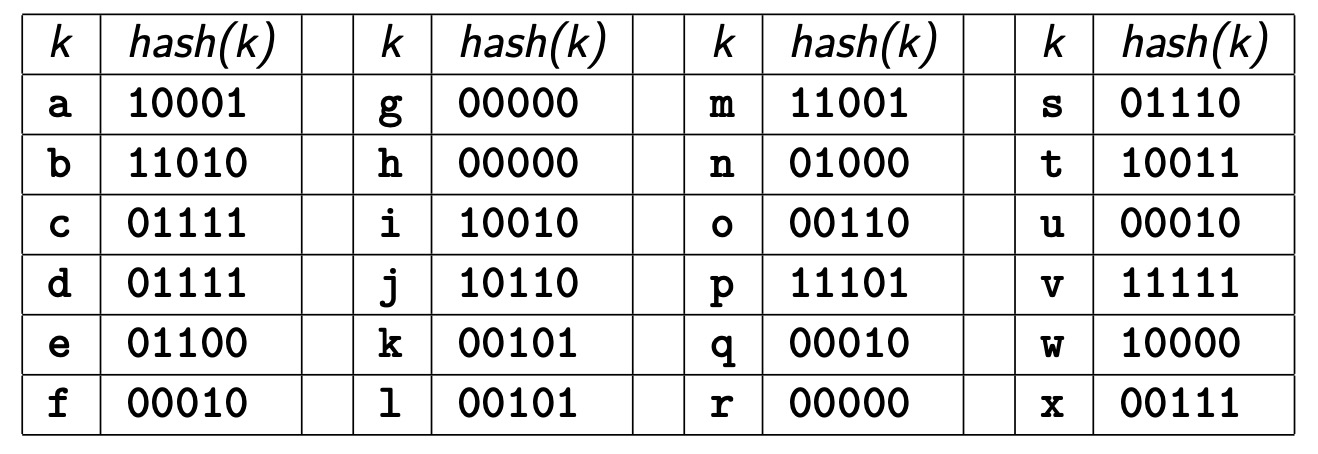
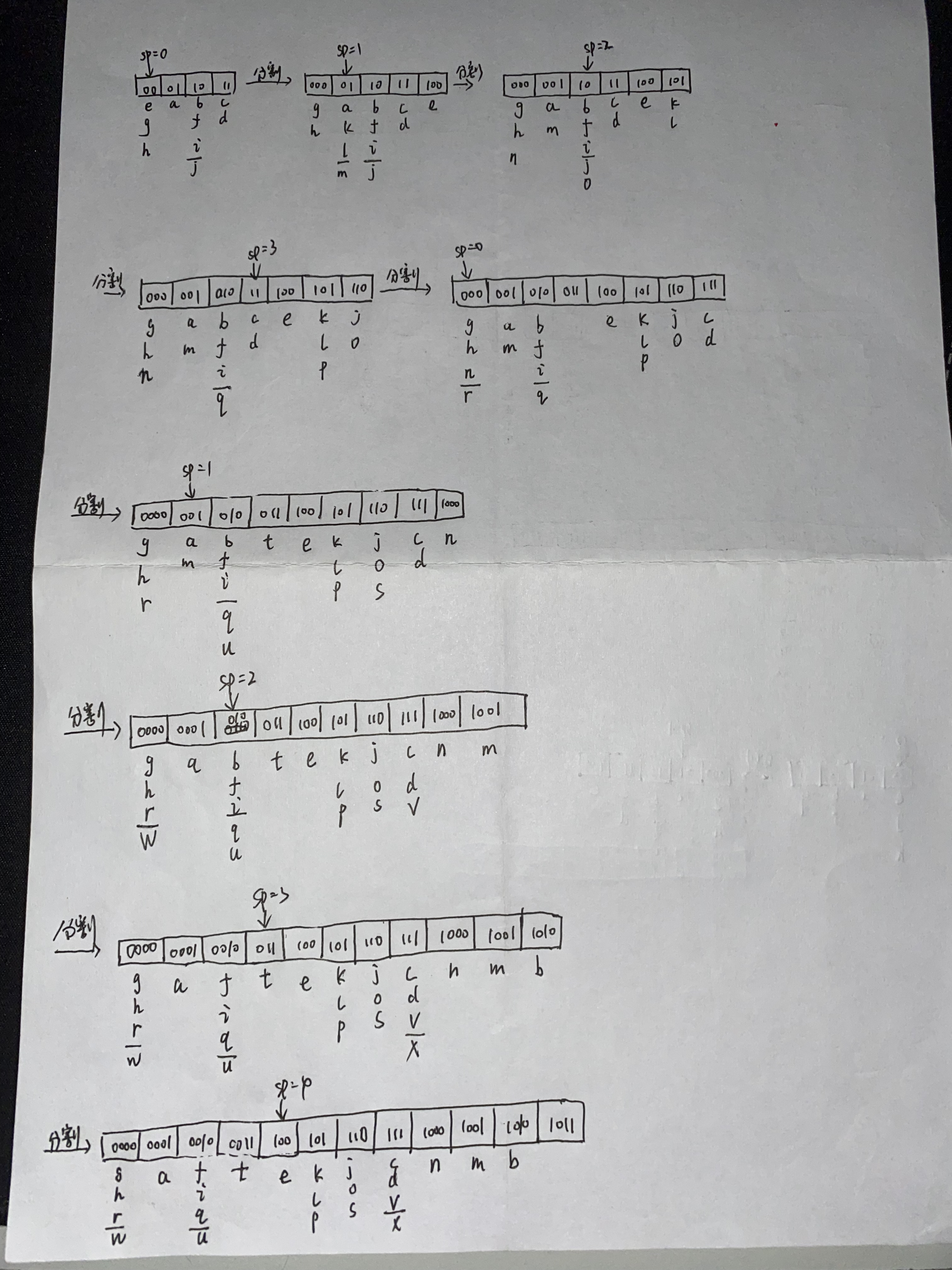
PostgreSQL 中的 Hash Files

PostgreSQL 在以下表上使用线性哈希：create index Ix on R using hash (k);

哈希文件的实现在 backend/access/hash 目录下：

• hashfunc.c：包含所需的哈希函数
• hashinsert.c：插入操作，包括溢出页面
• hashpage.c：一个工具函数和用于分割的函数
• hashsearch.c：哈希文件的搜索相关的函数

PostgreSQL 使用略微不同的文件组织：

• 一个文件包含了 Header (Metadata)，Main (Regular Data Pages), Overflow Pages
• Main Pages 分为多个组，每个组的尺寸为 \(2^n\)
• 在 Header 中保存了指向这多个组的 Pointers
• 每个 Pointer 指向每个组的开头

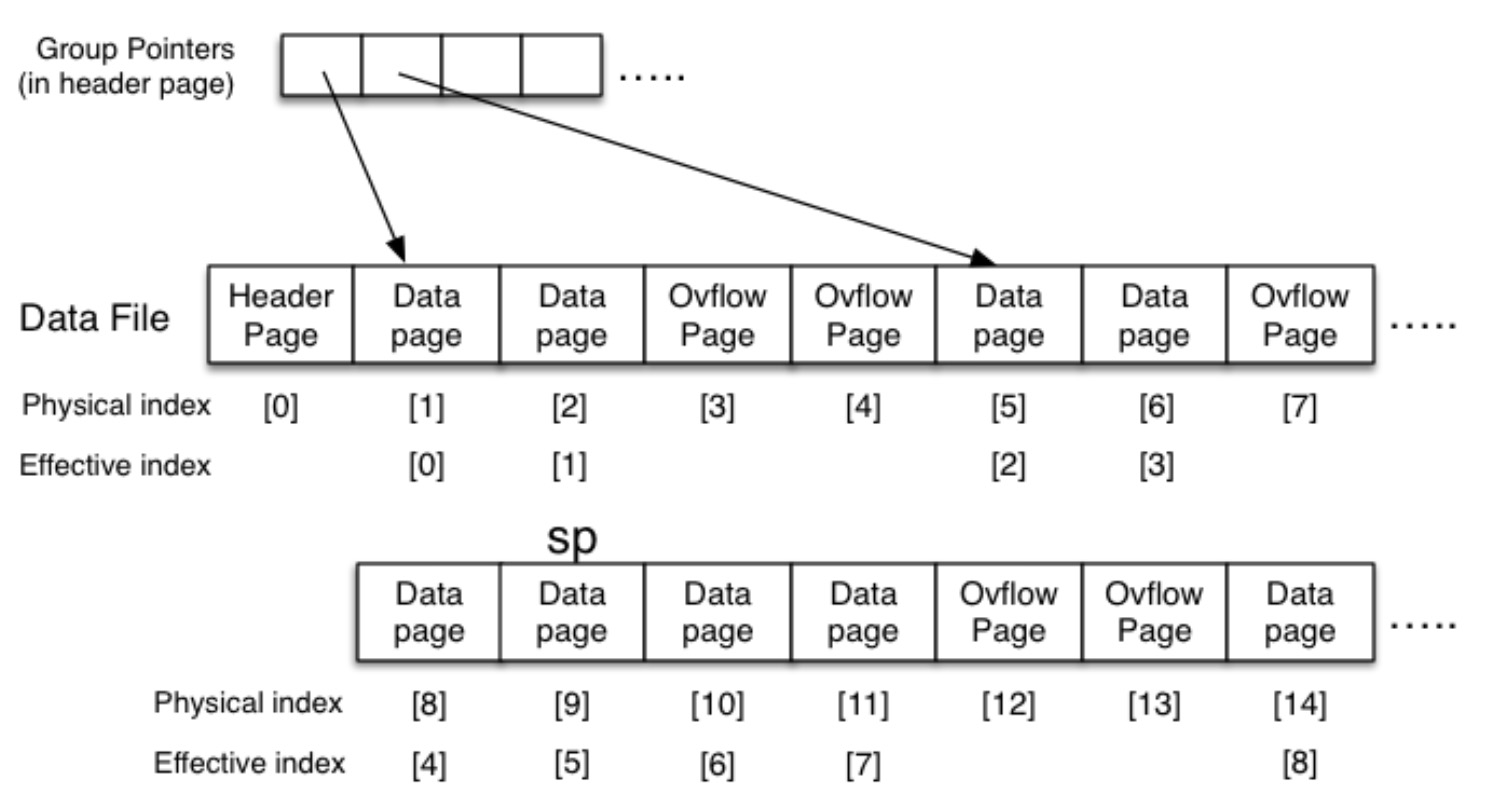
物理索引和 Bucket 索引实际上是不同的。我们需要一个函数将 Bucket Index 转换为物理索引。

// which page is primary page of bucket`
uint bucket_to_page(headerp, B) {
	uint *splits = headerp->hashm_spares;
	uint chunk, base, offset, lg2(uint);
	chunk = (B<2) ? 0 : lg2(B+1)-1;
	base = splits[chunk];
	offset = (B<2) ? B : B-(1<<chunk);
	return (base + offset);
}
// returns ceil(log_2(n))
int lg2(uint n) {
	int i, v;
	for (i = 0, v = 1; v < n; v <<= 1) i++;
	return i;
}