数据库内核:PostgreSQL 关系操作与评估
关系操作
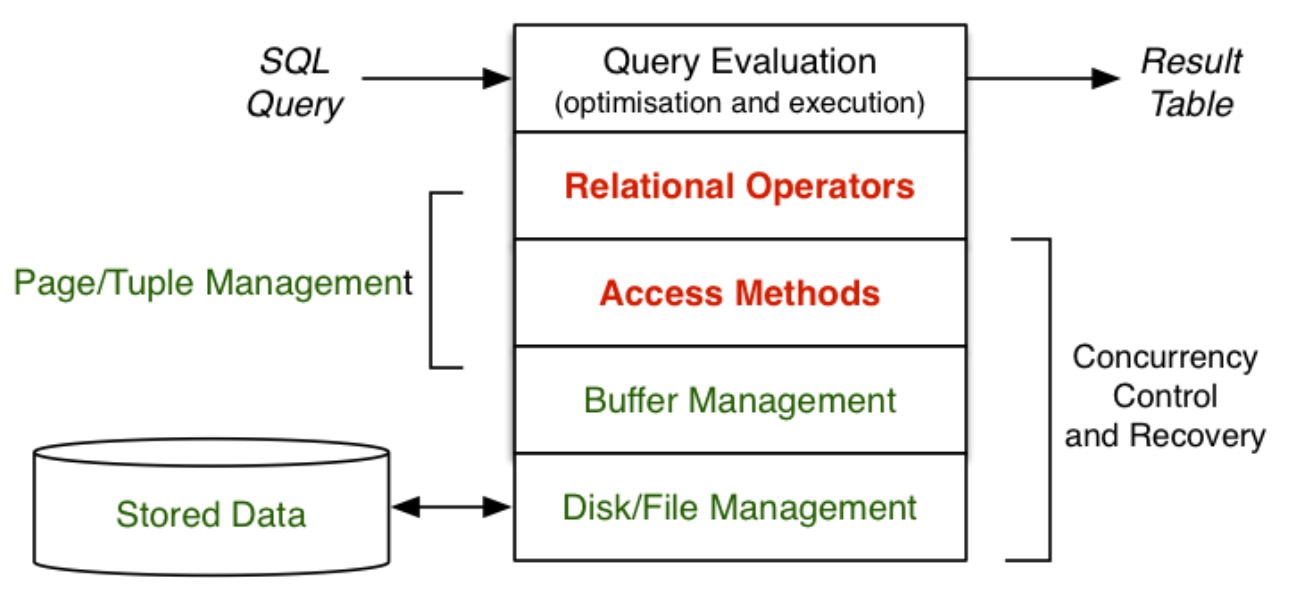
关键术语:
- 元组(tuple)= 在某些模式下收集数据值 \(\cong\) 记录(record)
- 页(page)= 块(block)= 元组集合 + 管理数据 = 输入/输出(I/O)的基本单元
- 关系(relation)= 表(table)\(\cong\) 文件(file)= 元组集合
两个维度:
- 关系操作(选择、投影、关联、排序等等)
- 访问方法(文件结构:堆、索引、哈希等等)
每个查询方法都涉及一个运算符和一个文件结构,除了查询成本外,还要考虑更新成本(插入/删除)。
成本分析
成本模型
成本可以用以下两个方面进行衡量
- 时间成本:执行方法所需的总时间
- 页面成本:页面读写的数量
成本模型的前提假设
- 内存(RAM)是小的,快速的,读取是以字节为单位的
- 磁盘存储是非常大,速度慢,读取是以分页为单位的
- 每个页面请求都会导致一些 I/O
- 一个关系有 \(r\) 个元组,每个元组平均大小为 \(R\) 字节
- 一个关系的所有元组存储在磁盘中需要 \(b\) 个数据页面
- 每个页面 \(B\) 字节,包含 \(c\) 个元组
- 查询 \(q\) 的结果元组集包含在 \(b_q\) 这几个数据页面中
- 数据是以整张页面在磁盘和内存之间传输的,其成本 \(T_{r/w}\) 很高
时间成本的影响因素
- I/O 设备的读取速度
- 不同机器速度不一样
因此,不考虑成本模型不考虑时间成本。用页面成本来比较方法会更好。但是页面成本的估计会受缓冲区的影响,所以通过多个并发操作和缓冲来估算成本会很困难。
文件结构的例子
在描述文件结构时,用一个大盒子来表示一个页面,使用小盒子或 \(tup_i\)(或 \(rec_i\))来表示元组,有时也通过它们的键来表示元组。大多数情况下,键对应于“主键”的概念,有时,在选择条件下键意味着“搜索键”。
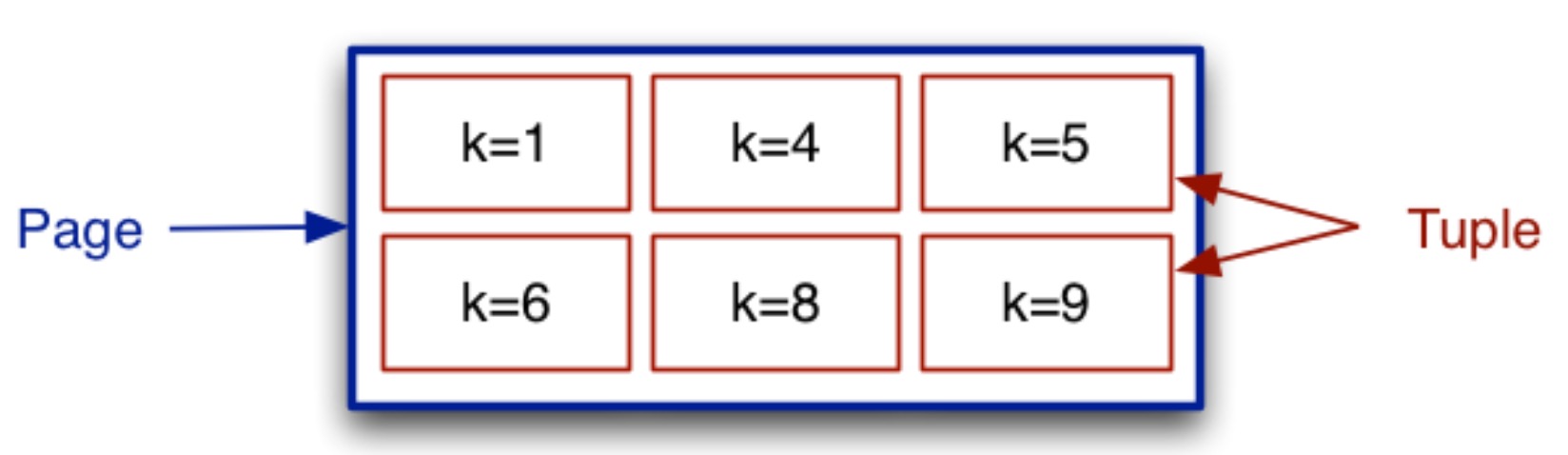
考虑三种简单的文件结构:
- heap file:元组添加到任意有空间的页面中
- sorted file:元组按照键的顺序在文件中排列
- hash file:元组根据哈希函数的值存放在页面中
所有的文件都由 \(b\) 个主要块/页构成,每个页中的一些记录被标记为 “deleted”。
操作成本例子
问题描述
假设一个文件头部包含了 \(r,R,b,B,c\) 和可用空间的第一页索引(和可用空间列表)。每个页面都包含一个标题和目录以及元组,没有缓冲区。
对于 heap file、sorted file、hash file 三种文件结构,插入和删除操作带来的页面读与写次数分别是多少?
heap file
假设 \(b=4,c=4\):
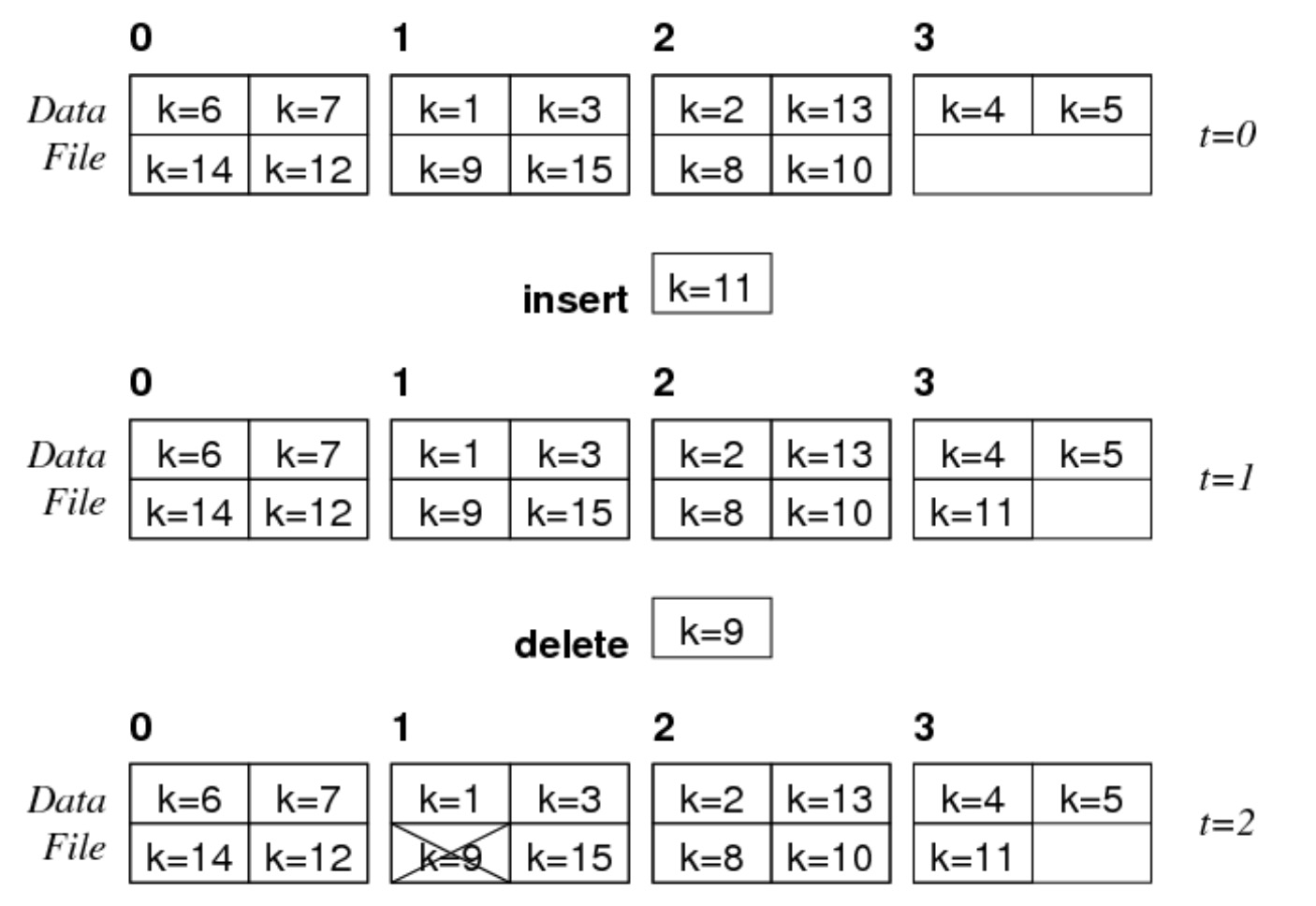
- 当插入一个元组时,直接插入到第一个空闲的位置中
- 当删除一个元组时,直接给元组打上删除的标记
sorted file
假设 \(b=4,c=4\):
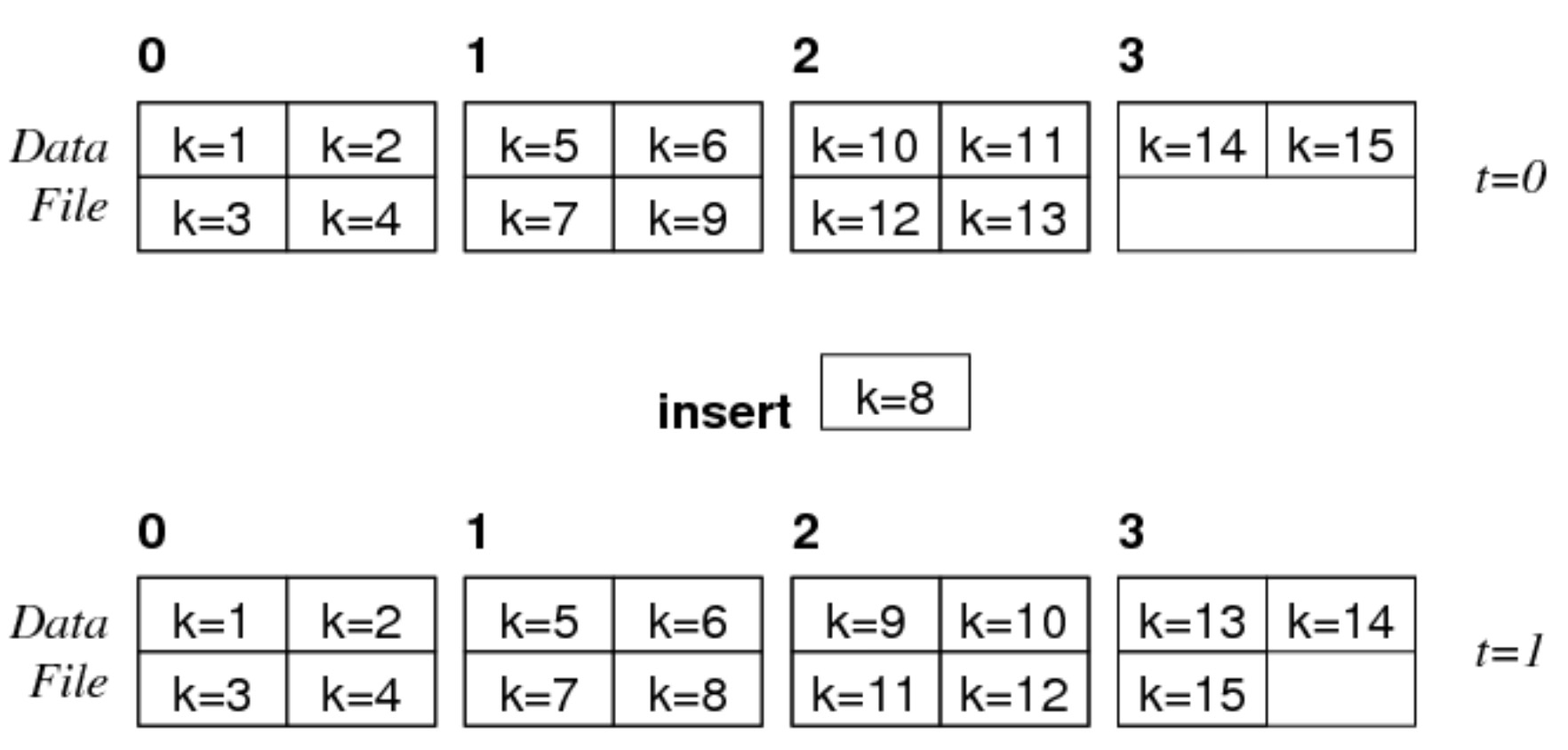
- 当插入一个元组时,需要保证键的顺序,因此要将键大于 8 的元组都往后挪一个元组的位置
- 删除同 heap file
hash file
假设 \(b=3,c=4,h(k)=k%3\):
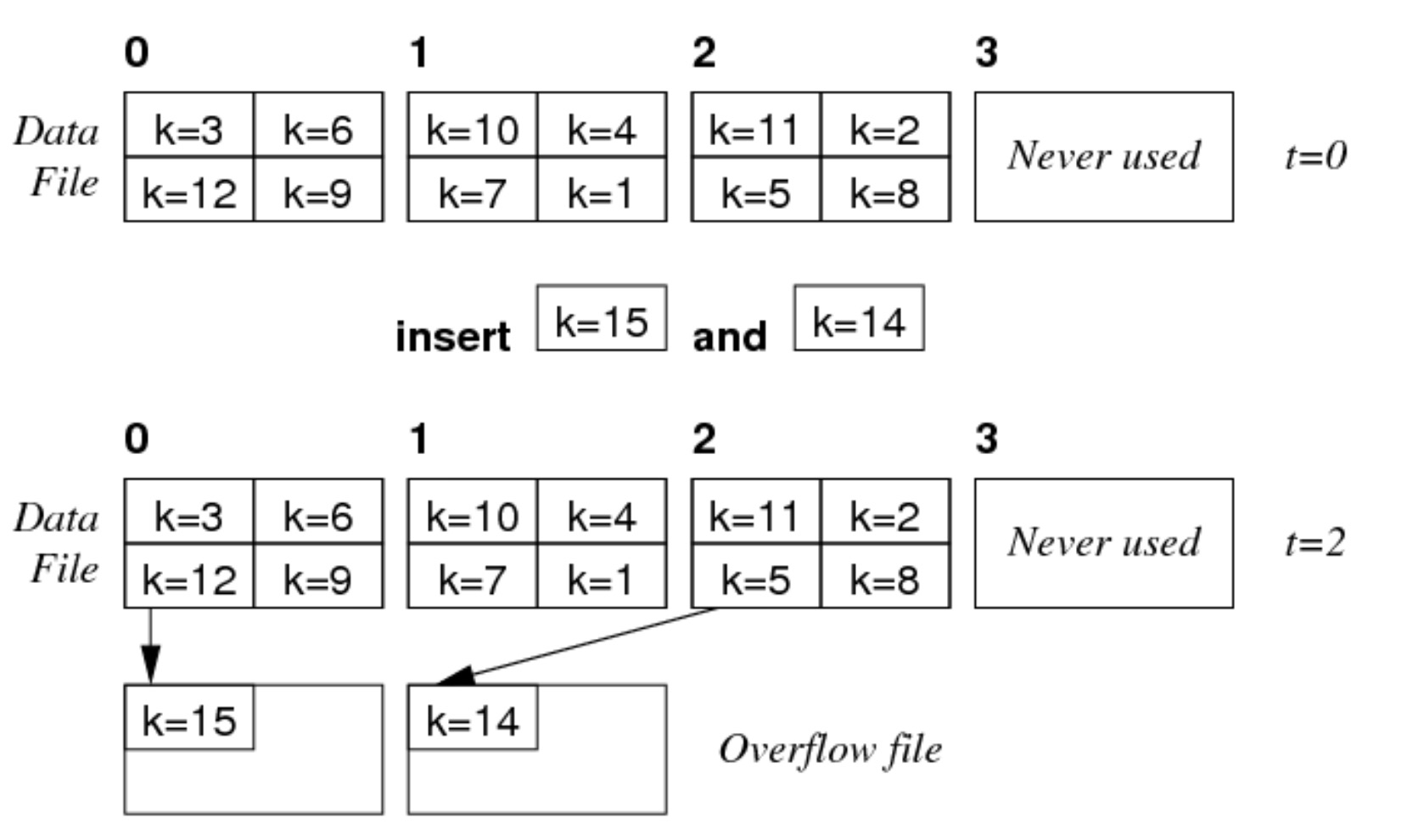
- 当插入键为 15 的元组时,其哈希值为 0,需要插入到索引为 0 的页中,但是该页面已经满了,所以插入相应的溢出页面。
- 删除同 heap file
扫描(Scanning)
select * from Rel;
这个查询操作的伪代码:
for each page P in file of relation Rel {
for each tuple t in page P {
add tuple t to result set
}
}
成本分析:每个页面读取一次,其时间成本为 \(b\cdot T_r\),页面成本 \(b\)(读取 \(b\) 个页面)。
当文件有溢出页面,扫描的方式如下:
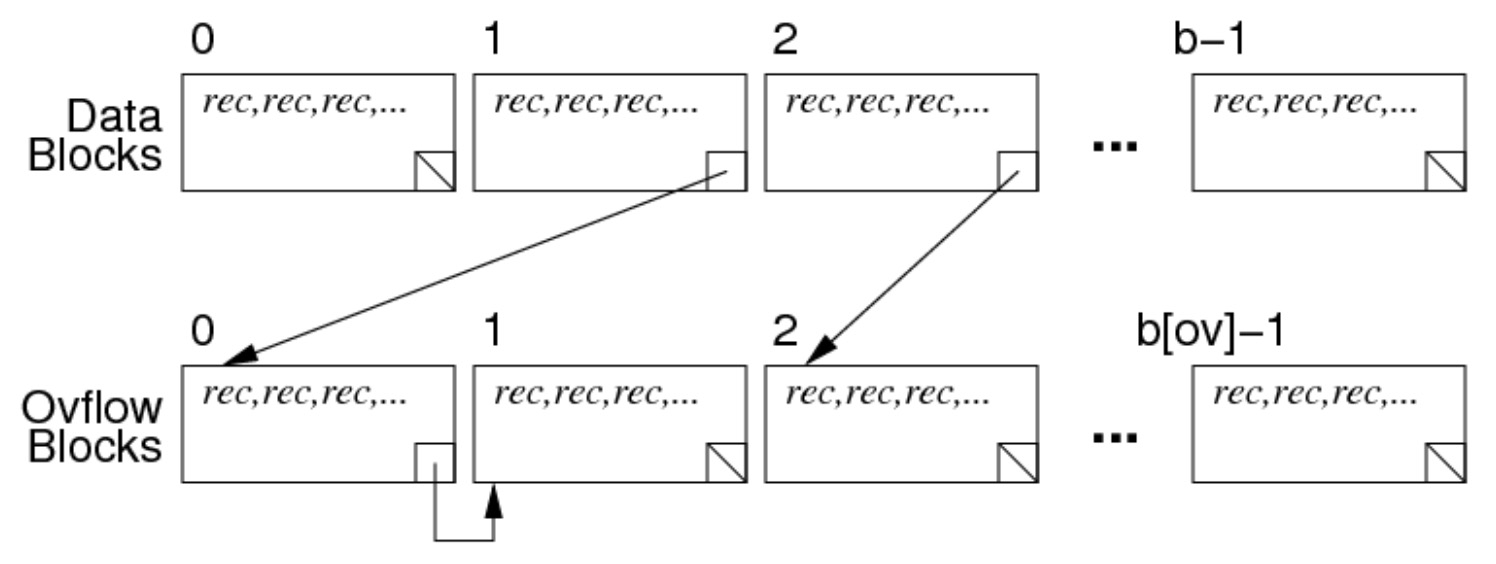
首先按顺序扫描页面,如果当前页面结尾有指向溢出页面的地址,则扫描溢出页面中的内容(溢出页面可以有多个),扫描完之后回到主线继续扫描。
因此,对于存在溢出页面的查询操作伪代码如下:
for each page P in data file of relation Rel {
for each tuple t in page P {
add tuple t to result set
}
for each overflow page V of page P {
for each tuple t in page V {
add tuple t to result set
}
}
}
成本分析:每个页面和溢出页面都读取一次,其页面成本为 \(b+b_{ov}\)
select * from Employee where id = 762288;
在没有顺序的文件中,搜寻满足查询的元组方式:

该查询的伪代码如下:
for each page P in relation Employee {
for each tuple t in page P {
if (t.id == 762288) return t
}
}
成本分析:
- 最好情况:读第一个页面就找到结果
- 最差情况:读到最后一个页面才找到结果(或者没找到),需要读 \(b\) 个页面
- 平均情况:读取一半的页面 \(\frac{b}{2}\)
因此,页面成本:\(Cost_{avg}=\frac{b}{2},Cost_{min}=1,Cost_{max}=b\)
哈希文件的搜索成本
假设哈希文件中 \(b=10,c=4,h(k)=k\%10\)

对于查询语句 select * from R where k = 51;:
- \(h(51)=51\%10=1\),因此只需要扫描索引为 1 的页面以及相应的溢出页面。
- 最好的情况就是索引为 1 的第一个页面就找到了,最差情况是读遍索引为 1 的页面及其溢出页面。
对于查询语句 select * from R where k > 50;:
- 则需要扫描所有页面和溢出页面。
- 最好情况,读索引为 0 的第一个页面就找到结果,最差情况遍历所有的页面和溢出页面。
迭代器
扫描通常会使用迭代器:
Scan s = start_scan(Relation r, ...):开始扫描关系 r,扫描可能包括实现 WHERE 的条件,通过文件保存进度数据(例如当前页面)。Tuple next_tuple(Scan s):返回上次访问的元组之后的元组,如果关系中没有更多元组,则返回 NULL。
以 select name from Employee 为例,其实现如下:
DB db = openDatabase(”myDB”);
Relation r = openRelation(db,”Employee”,READ);
Scan s = start_scan(r);
Tuple t; // current tuple
while ((t = next_tuple(s)) != NULL)
{
char *name = getStrField(t,2);
printf(”%s\n”, name);
}
其中 Scan 的数据结构如下:
typedef struct {
Relation rel;
Page *curPage; // Page buffer
int curPID; // current pid
int curTID; // current tid
} ScanData;
关系复制
例如执行 create table T as (select * from S); 语句时,其伪代码如下:
make empty relation T
s = start scan of S
while (t = next_tuple(s)) {
insert tuple t into relation T
}
复制之后,T 关系可能比 S 关系所占页面要少。因为 S 关系中未使用的可用空间(元组被移除的空间)会被重新利用,因此 T 关系是紧凑的。
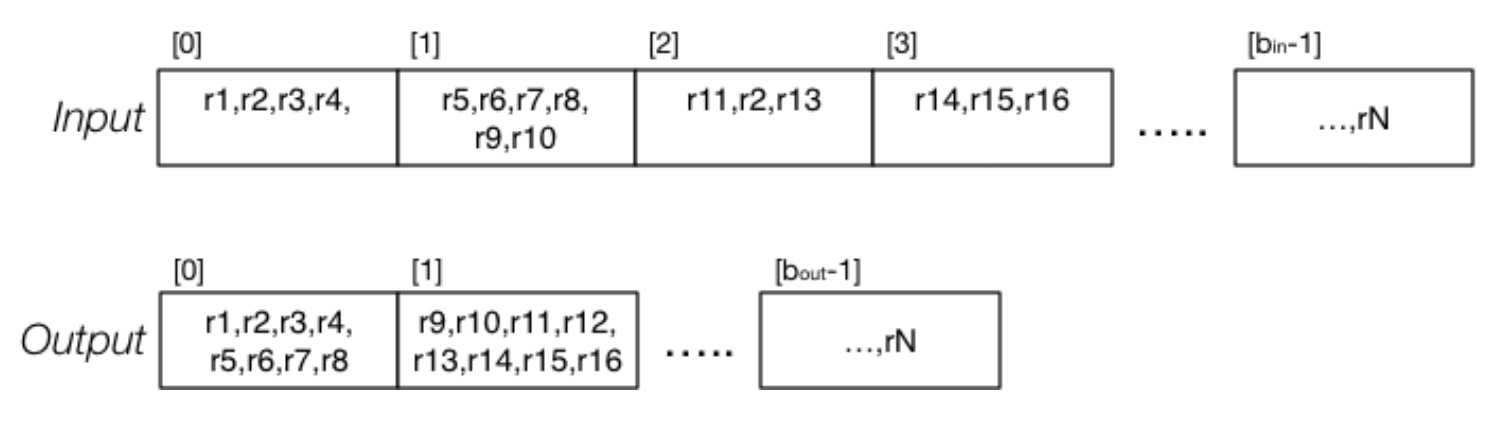
就现有关系/页面/元组操作而言,关系复制操作的代码如下:
Relation in; // 输入关系
Relation out; // 输出关系
int ipid,opid,tid; // 页面和记录遍历所需的索引
Record rec; // 当前元组
Page ibuf,obuf; // 输入/输出文件缓冲区
in = openRelation(”S”, READ);
out = openRelation(”T”, NEW|WRITE);
clear(obuf);
opid = 0;
for (ipid = 0; ipid < nPages(in); ipid++) {
ibuf = get_page(in, ipid); // 获取页面
for (tid = 0; tid < nTuples(ibuf); tid++) {
rec = get_record(ibuf, tid); // 获取元组
if (!hasSpace(obuf,rec)) { // 检查输出缓冲区 obuf 是否有足够的空间容纳当前记录 rec
put_page(out, opid++, obuf); // 如果输出缓冲区空间不足,将输出缓冲区的内容写入目标关系的页面,并清空输出缓冲区。
clear(obuf);
}
insert_record(obuf,rec);
}
}
if (nTuples(obuf) > 0) put_page(out, opid, obuf);
假设:输入文件有 r 个元组,每页有 c 个元组,\(b_{in}\) 表示输入文件的页面数,输入文件的某些页面并不是填满的,而输出文件希望所有页面都是满的(最后一页可以不满)。
成本分析:
- 如果输入和输出文件的结构都是 heap file,输入文件的页面数量为 \(b_{in}\),也就是说要读 \(b_{in}\) 个页面,而写页面的数量则为 \(\lceil r/c \rceil\),因此成本为 \(b_{in}+\lceil r/c \rceil\)。
- 如果输入文件结构是 sorted file,输出文件结构是 heap file,成本同上一种情况。
- 如果输入文件结构是 heap file,输出文件结构是 sorted file,???
Scanning 在 PostgreSQL 中的实现
backend/access/heap/heapam.c- 实现迭代器数据/操作
HeapScanDesc:包含迭代状态的结构scan = heap_beginscan(rel,...,nkeys,keys):扫描 heap 第一个元组tup = heap_getnext(scan, direction):获取下一个扫描元组heap_endscan(scan):释放扫描结构res = HeapKeyTest(tuple,...,nkeys,keys):在元组上执行 ScanKeys 测试,判断它是否为结果元组
typedef HeapScanDescData *HeapScanDesc; // 堆扫描的描述符
typedef struct HeapScanDescData {
Relation rs_rd; // 要扫描的堆关系
Snapshot rs_snapshot; // 确定扫描期间的元组可见性
int rs_nkeys; // 确定扫描期间的元组可见性
ScanKey rs_key; // 扫描时的过滤条件
...
PageNumber rs_npages; // 扫描的页面总数
PageNumber rs_startpage; // 从哪个页面开始进行扫描
...
HeapTupleData rs_ctup; // 当前在扫描中的元组
PageNumber rs_cpage; // 当前正在扫描的页面
Buffer rs_cbuf; // 当前在扫描中使用的缓冲区
...
} HeapScanDescData;
排序(Sorting)
排序在其他操作中内部使用的作用:
- 在投影中消除重复元组
- 排序文件以提高选择的效率
- 实现各种风格的连接
- 在
group by中形成元组分组
快速排序等排序方法是为内存数据设计的。对于磁盘上的大型数据,需要外部排序,如归并排序。
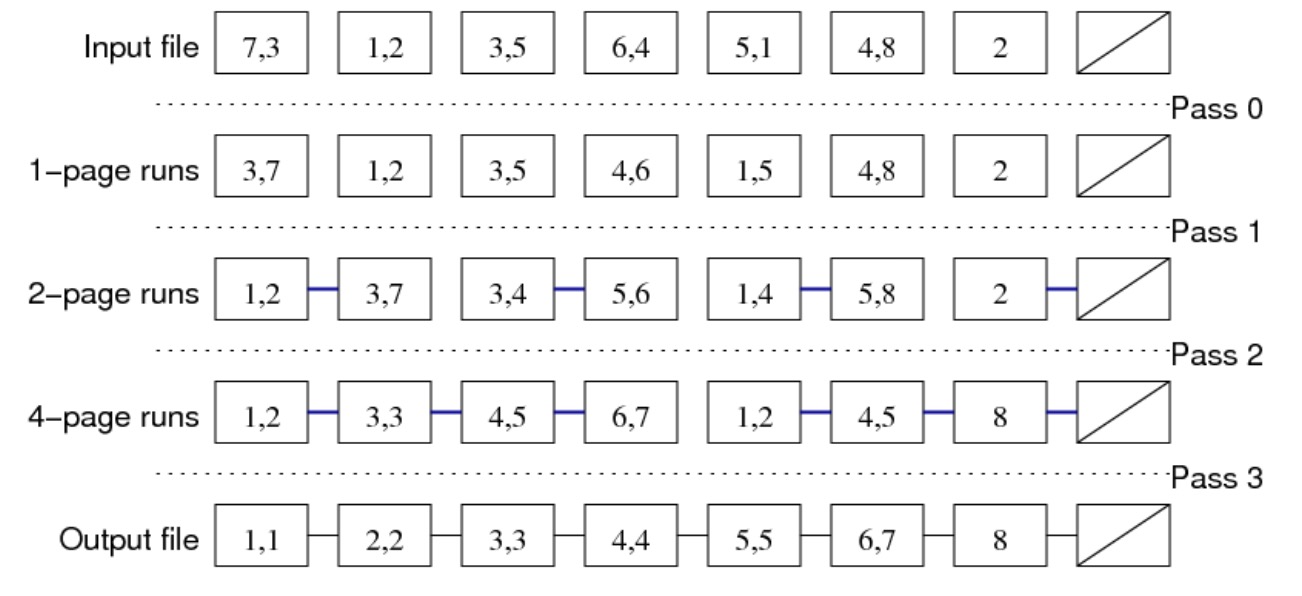
二路归并排序
内存中至少需要三个缓冲区:
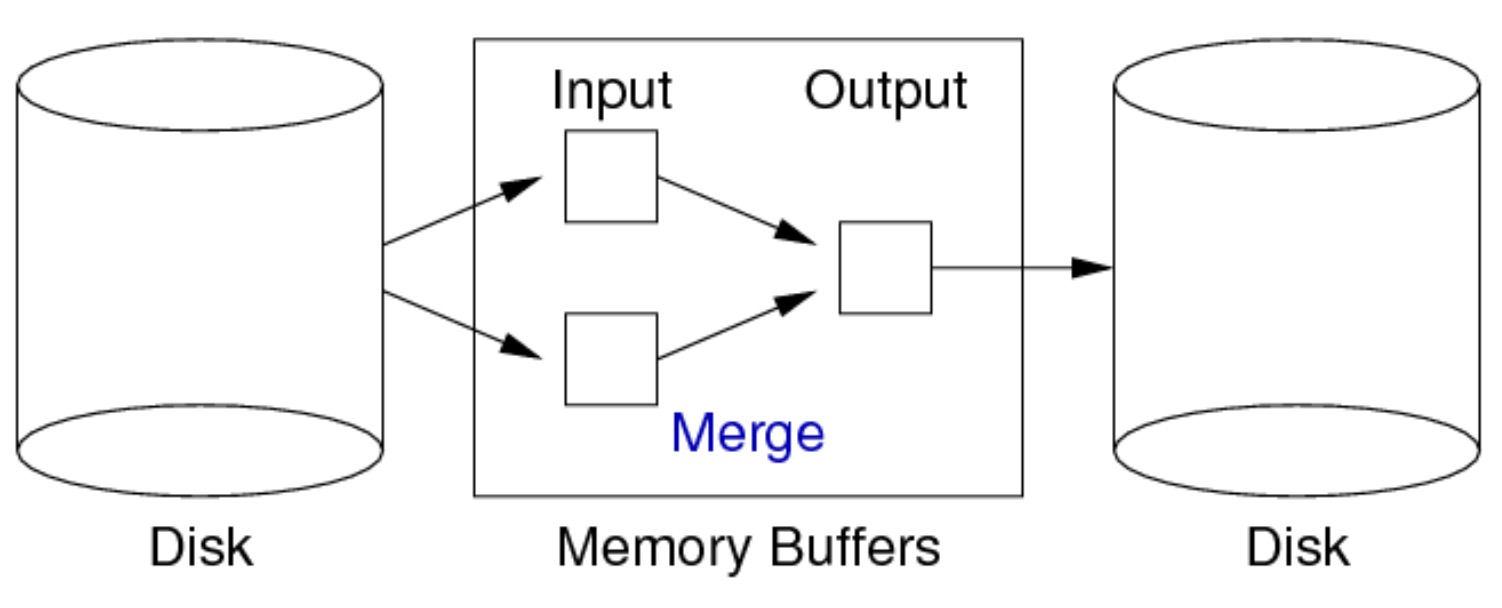
假设两个缓冲区进行归并的成本为 0,归并时的函数如下:
int tupCompare(r1,r2,f)
{
if (r1.f < r2.f) return -1;
if (r1.f > r2.f) return 1;
return 0;
}
实际上,需要对多个属性进行排序,并且排序分为 ASC/DESC,例如以下 SQL:
select * from Students
order by age desc, year_enrolled
多属性排序函数的简易代码如下:
int tupCompare(r1,r2,criteria) {
foreach (f,ord) in criteria {
if (ord == ASC) {
if (r1.f < r2.f) return -1;
if (r1.f > r2.f) return 1;
}
else {
if (r1.f > r2.f) return -1;
if (r1.f < r2.f) return 1;
}
}
return 0;
}
成本分析:对于一个包含 \(b\) 个页面的文件,需要 \(ceil(log_2b)\) 轮排序,每一轮需要读取 \(b\) 个页面,写出 \(b\) 个页面。因此总成本为 \(2b\cdot\lceil log_2b\rceil\)。
n 路归并排序
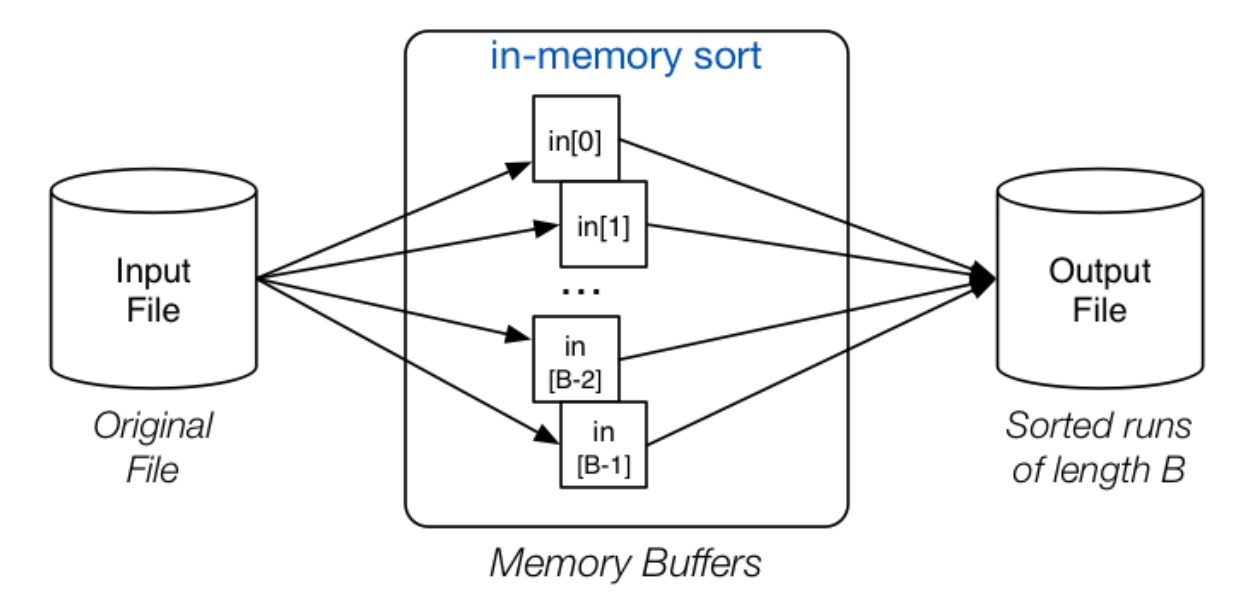
在这一轮操作中,使用全部的 B 个 Buffer 来读取文件中的 pages,之后对读取的这些 pages 进行内排序,之后将排序后的结果整体打包,存入文件,该文件中,每一个 Run 的尺寸即为 B pages。这一环节就被称为初始 Runs 的生成。输出文件中会有 \(\lceil\frac{b}{B}\rceil\) 个这样的 Runs。
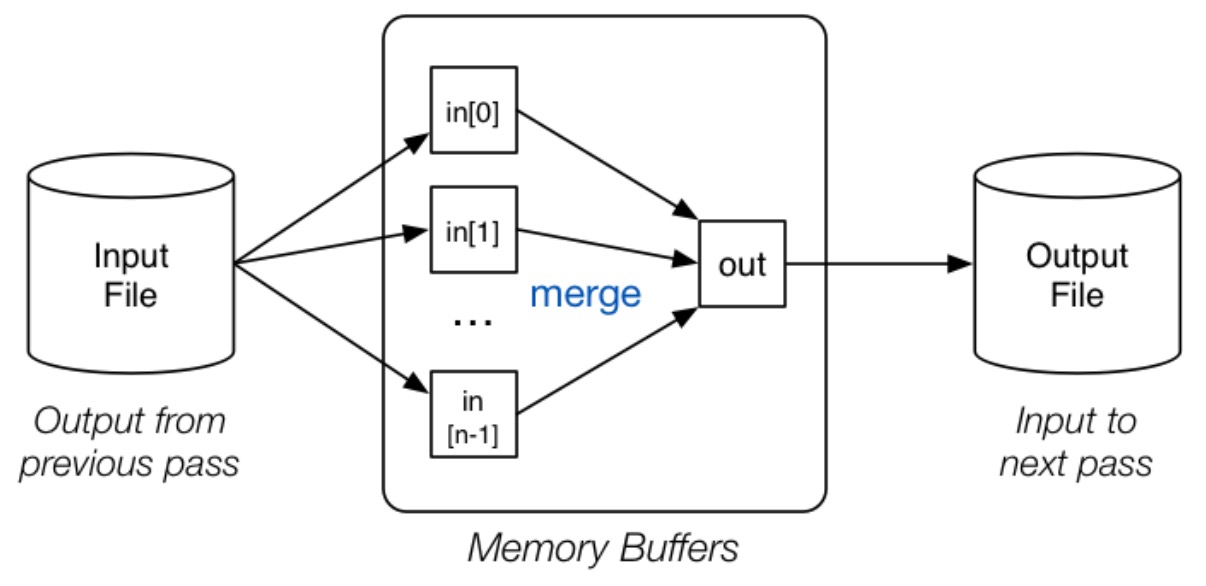
接下来,进行递归的合并操作。此时不再使用全部的 B 个 Buffer,而是使用 B- 1 个 Buffer,这样将 B - 1 个 Runs 进行合并,得到一个新的排好序的 Run,也就是 B-1 路归并,每个新的 Run 的尺寸即为 B*(B - 1) Pages。之后不断重复此操作,最终得到一个排好序的文件。
// 分组,每次 B 个页面,将页面中的元组进行排序并写出到Temp临时文件
for each group of B pages in Rel {
read B pages into memory buffers
sort group in memory
write B pages out to Temp
}
// 归并
numberOfRuns = ceil(b/B) // 进行归并的运行组数
while (numberOfRuns > 1) {
// 进行 n 路归并操作,n = B - 1
for each group of n runs in Temp {
merge into a single run via input buffers
write run to newTemp via output buffer
}
numberOfRuns = ceil(numberOfRuns/n) // 按照 n 路归并后的运行组数重新计算
Temp = newTemp // 使新的临时文件成为下一次归并的输入文件
}
成本分析:
例子:假设 \(b=4096,B=16\),也就是说 4096 个页面,16 个缓冲区。
- 第 0 轮:进行排序,256 个 Runs,每个 Run 的尺寸为 16 个页面
- 第 1 轮:对尺寸为 16 个页面的 Runs 进行 15 路归并,得到 18 个新 Runs,其尺寸为 240 个页面
- 第 2 轮:对尺寸为 240 个页面 Runs 进行 15 路归并,得到 2 个新 Runs,其尺寸为 3600 个页面
由上面的例子总结可以得到以下结论,对于 \(b\) 个数据页面,\(B\) 个缓冲区:
- 第 0 轮:读/写 \(b\) 个页面,得到 \(b_0=\lceil\frac{b}{B}\rceil\) Runs
- 接下来需要进行 \(\lceil log_nb_0\rceil\) 轮排序,这里的 \(n=B-1\),表示 n 路归并,每一轮排序都需要读/写 \(b\) 个页面。
因此,总的成本为 \(2b(1+\lceil log_nb_0\rceil)\)。
练习题
前提条件:
- \(r=1048576=2^{20}\) 个元组
- 每个元组 \(R=62\) 字节(固定大小)
- 每个页面 \(B=4096\) 字节
- 每个页面的头部信息占 \(H=96\) 字节
- 页面目录中为每个元组使用 \(D=1\) 个存在位
第一问:当存在 \(B=9\) 个缓冲区,其中 8 个作为输入缓冲区,1 个作为输出缓冲区,此时成本为多少?
解:每个页面除去头部信息,用于存元组的空间为 4000 字节,可以存 64 个元组(64 比特+64*64字节不大于4000字节)。因此,需要 \(b=16384\) 个页面。\(b_0=\lceil\frac{b}{B}\rceil=\lceil\frac{16384}{9}\rceil=1821\),\(n=8\),带入成本公式 \(2b(1+\lceil log_nb_0\rceil)=2*16384*(1+\lceil log_81821\rceil)=163840\)
第二问:当存在 \(B=33\) 个缓冲区,其中 32 个作为输入缓冲区,1 个作为输出缓冲区,此时成本为多少?
解:\(b_0=\lceil\frac{b}{B}\rceil=\lceil\frac{16384}{33}\rceil=497\),\(n=32\),带入成本公式 \(2b(1+\lceil log_nb_0\rceil)=2*16384*(1+\lceil log_{32}497\rceil)=98304\)
第三问:当存在 \(B=257\) 个缓冲区,其中 256 个作为输入缓冲区,1 个作为输出缓冲区,此时成本为多少?
解:\(b_0=\lceil\frac{b}{B}\rceil=\lceil\frac{16384}{257}\rceil=64\),\(n=256\),带入成本公式 \(2b(1+\lceil log_nb_0\rceil)=2*16384*(1+\lceil log_{256}64\rceil)=65536\)
投影(Projection)
当执行 select distinct name,age from Employee; 语句时,如果 Employee 关系表如下:
(94002, John, Sales, Manager, 32)
(95212, Jane, Admin, Manager, 39)
(96341, John, Admin, Secretary, 32)
(91234, Jane, Admin, Secretary, 21)
那么返回的结果为:
(Jane, 21) (Jane, 39) (John, 32)
这里的 (John,32) 有重复,只会保留一个(如果使用 distinct 关键词),可以用 sorting 或者 hashing 两种方式来实现。
基于排序的投影
需要一个临时文件/关系
for each tuple T in Rel {
T’ = mkTuple([attrs],T)
write T’ to Temp
}
sort Temp on [attrs]
for each tuple T in Temp {
if (T == Prev) continue
write T to Result
Prev = T
}
练习:考虑以下 \(R(x,y,z)\) 关系
Page 0: (1,1,’a’) (11,2,’a’) (3,3,’c’)
Page 1: (13,5,’c’) (2,6,’b’) (9,4,’a’)
Page 2: (6,2,’a’) (17,7,’a’) (7,3,’b’)
Page 3: (14,6,’a’) (8,4,’c’) (5,2,’b’)
Page 4: (10,1,’b’) (15,5,’b’) (12,6,’b’)
Page 5: (4,2,’a’) (16,9,’c’) (18,8,’c’)
假设执行 SQL create T as (select distinct y from R),3 个缓冲区,2 个输入缓冲区,1 个输出缓冲区。页面和缓冲区都可以放 \(c_R=3\) 个 R 关系的元组,\(c_T=6\) 个元组。
基于排序的投影过程:首先,遍历 R 关系的元组并且进行投影写入临时文件中,结果如下:
Page 0: (1) (2) (3) (5) (6) (4)
Page 1: (2) (7) (3) (6) (4) (2)
Page 2: (1) (5) (6) (2) (9) (8)
然后进行排序,结果如下:
Page 0: (1) (1) (2) (2) (2) (2)
Page 1: (3) (3) (4) (4) (5) (5)
Page 2: (6) (6) (6) (7) (8) (9)
然后再从头遍历到尾,过滤掉与前一个元组相同的元组,结果如下:
Page 0: (1) (2) (3) (4) (5) (6)
Page 1: (7) (8) (9)
成本分析,假设有 \(B=n+1\) 个缓冲区用于排序:
- 扫描原始关系成本:\(b_R=6\)
- 写入临时关系成本:\(b_T=3\)
- 对临时关系进行排序成本:\(2b_T(\lceil log_nb_0\rceil)=2*3*\lceil log_{2}(6/3)\rceil=6\)
- 扫描临时关系,并排出重复元组成本:\(b_T=3\)
- 写出结果成本:\(b_{out}=2\)
总成本就是所有相加即可。
基于哈希的投影
分区阶段:
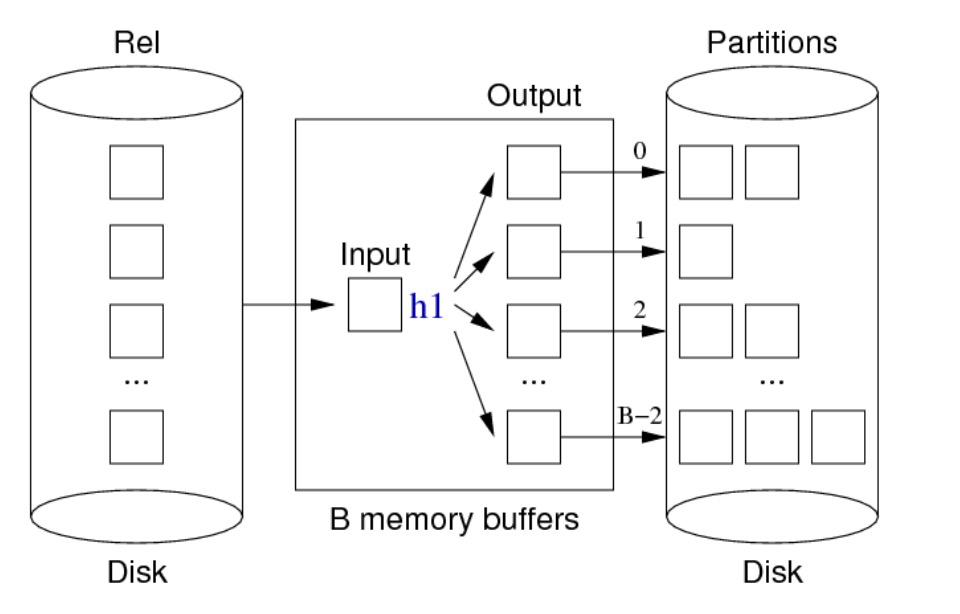
重复元组过滤阶段:
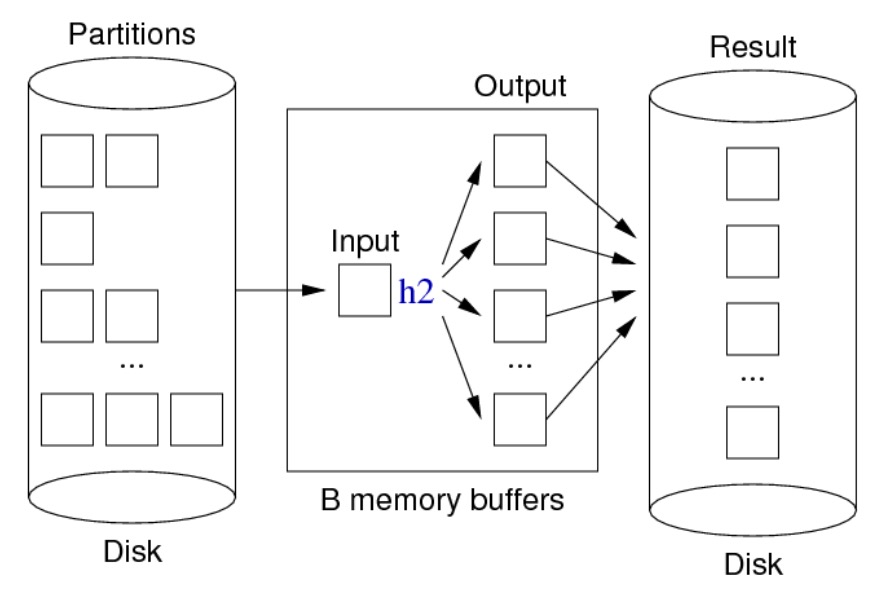
伪代码:
for each tuple T in relation Rel {
T’ = mkTuple([attrs],T)
H = h1(T’, n)
B = buffer for partition[H]
if (B full) write and clear B
insert T’ into B
}
for each partition P in 0..n-1 {
for each tuple T in partition P {
H = h2(T, n)
B = buffer for hash value H
if (T not in B) insert T into B
// assumes B never gets full
}
write and clear all buffers
}
练习:考虑以下 \(R(x,y,z)\) 关系
Page 0: (1,1,’a’) (11,2,’a’) (3,3,’c’)
Page 1: (13,5,’c’) (2,6,’b’) (9,4,’a’)
Page 2: (6,2,’a’) (17,7,’a’) (7,3,’b’)
Page 3: (14,6,’a’) (8,4,’c’) (5,2,’b’)
Page 4: (10,1,’b’) (15,5,’b’) (12,6,’b’)
Page 5: (4,2,’a’) (16,9,’c’) (18,8,’c’)
假设执行 SQL create T as (select distinct y from R),4 个缓冲区,3 个用于分区 ,1 个用于输入。页面和缓冲区都可以放 \(c_R=3\) 个 R 关系的元组,\(c_T=4\) 个元组。哈希函数 \(h_1(k)=k\%3,h_2(k)=(k\%4)\%3\).
基于哈希的投影过程:首先,根据哈希值进行分区,得到结果如下:
分区 0:
Page 0: (3) (6) (3) (6)
Page 1: (6) (9)
分区 1:
Page 0: (1) (4) (7) (4)
Page 1: (1)
分区 2:
Page 0: (2) (5) (2) (2)
Page 1: (5) (2) (8)
然后逐个对每个分区的每个页面进行过滤操作,结果如下:
# 对第一个分区进行过滤
分区 0:
Page 0: (3)
分区 1:
Page 0: (9)
分区 2:
Page 0: (6)
# 对第二个分区进行过滤
分区 0:
Page 0: (3) (4) (7)
分区 1:
Page 0: (9) (1)
分区 2:
Page 0: (6)
# 对第三个分区进行过滤
分区 0:
Page 0: (3) (4) (7) (8)
分区 1:
Page 0: (9) (1) (5)
分区 2:
Page 0: (6) (2)
成本分析,假设有 \(B=n+1\) 个缓冲区用于排序:
- 扫描原始关系成本:\(b_R=6\)
- 写分区成本:\(b_P=6\)
- 重新读分区成本:\(b_P=6\)
- 写出结果成本:\(b_{out}=3\)
总成本就是所有相加即可。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号