算法总结
前言:
有关于算法的一切的大合集
基本数据结构及排序方法手撸
-
完全二叉树/满二叉树
-
红黑树
- 节点分为红色或者黑色;
- 根节点必为黑色;
- 叶子节点都为黑色,且为null;
- 连接红色节点的两个子节点都为黑色(红黑树不会出现相邻的红色节点);
- 从任意节点出发,到其每个叶子节点的路径中包含相同数量的黑色节点;
- 新加入到红黑树的节点为红色节点;
-
AVL树
-
B树/B+树,为什么B+树做数据索引
-
B树:在非叶子节点中也存在值,搜索有可能直接结束。
-
B+树:非叶子节点不存储数据,固定为log n.并且支持范围查询,叶子节点之间有指针连接
-
B树只适合随机检索,而B+树同时支持随机检索和顺序检索;
优点:
- B+树空间利用率更高,(非叶子节点无值)
- B+树查询效率更加稳定(值都在叶子节点上)
- 范围查询更优:根据空间局部性原理:如果一个存储器的某个位置被访问,那么将它附近的位置也会被访问
- 增删文件效率更高
- B+树在一次IO里面,能读出的索引值更多。从而减少查询时候需要的IO次数!
-
-
sizeof指针大小?
对于32位系统,指针大小是4个字节,\(2^{32}\)约为\(4G\),对于64位系统,指针大小是8个字节,可寻址空间为\(2^{64}\).
-
\(\textcolor{OrangeRed}{内存对齐}\)
-
冒泡排序?是交换排序的一种,其他还有快速排序, 每次遍历相邻的两个元素,大元素往下沉
void bubbleSort(vector<int>& nums){ // 每次交换相邻的两个 bool flag = false; int n = nums.size(); for(int i=0; i<n; i++){ // 每次遍历将最大的元素移到最后 for(int j=0; j<n-i-1; j++){ if(nums[j] > nums[j+1]){ swap(nums[j], nums[j+1]); flag = true; } } if(!flag) break; } } -
插入排序?前面是已经排好序的数组,从后面未排序的数组中取第一个插入到前面排序数组中,然后依次将数值往后移动。
void insertionSort(vector<int>& nums) { int n = nums.size(); for(int i=1; i<n; ++i){ //已排好序的id (i-1) int value = nums[i]; int j = i-1; while(j >= 0 && nums[j] > value){ nums[j+1] = nums[j]; // 往后移动 j--; } nums[j+1] = key; } } -
选择排序?与插入排序有点相似,只不过实现从未排序数组中找一个最小元素插入到已排序的后面
void selectionSort(vector<int>& nums) { int n = nums.size(); for (int i = 0; i < n - 1; ++i) { // i是当前未排序的开头 int minIndex = i; for (int j = i + 1; j < n; ++j) { if (nums[j] < nums[minIndex]) { minIndex = j; } } if (minIndex != i) { swap(nums[i], nums[minIndex]); } } } -
归并排序?
void merge(vector<int>& nums, int low, int high, int mid){ // mid是属于前半部分 if(low >= high) return low; int i=low, j=mid+1; vector<int> temp(nums.size()); int index=low; while(i <= mid && j <= high){ if(nums[i] <= nums[j]){ temp[index++] = nums[i++]; } else { temp[index++] = nums[j++]; } } while(i <= mid) temp[index++] = nums[i++]; while(j <= high) temp[index++] = nums[j++]; // 再把temp复制到原数组中 for(int i=low; i<=high; i++){ nums[i] = temp[i]; } } void mergeSort(vector<int>& nums, int i, int j){ if(i >= j) return; int mid = i + (j - i) / 2; mergeSort(nums, i, mid); mergeSort(nums, mid+1, j); merge(nums, i, j, mid); } -
堆排序?
- 对某一个叶子节点的调整操作
- 从最后一个非叶子节点开始调整,直至建堆完成
- 每次互换堆根与堆尾
void maxHeapify(vector<int>& nums, int idx, int rangeLimit){ int lChild = idx*2+1 < rangeLimit ? idx*2+1: idx; int rChild = idx*2+2 < rangeLimit ? idx*2+2: idx; int maxId = nums[lChild] > nums[rChild] ? lChild: rChild; if(nums[idx] >= nums[maxId]) return; swap(nums[idx], nums[maxId]); maxHeapify(nums, maxId, rangeLimit); } void initHeap(vector<int> nums){ // 对每一个非叶子节点调整,调整好就是堆了 for(int i=nums.size()/2 - 1; i>=0; --i){ maxHeapify(nums, i, nums.size()); } } void headSort(vector<int> nums){ initHeap(nums); for(int i = nums.size()-1; i>0; --i){ // 首尾交换 swap(nums[0], nums[i]); maxHeapify(nums, 0, i); } }// 小根堆 void minHeapify(vector<int>& nums, int idx, int rangeLimit){// 小根堆化操作 // 调整某一个非叶子节点,直至不再调整 int l = 2 * idx + 1 < rangeLimit? 2*idx+1 : idx; int r = 2 * idx + 2 < rangeLimit? 2*idx+2 : idx; int minIdx = nums[l] <= nums[r] ? l: r; if(nums[idx] <= nums[minIdx]) return; swap(nums[idx], nums[minIdx]); minHeapify(nums, minIdx, rangeLimit); } void initHeap(vector<int>& nums){ // 初始化堆从最后一个非叶子节点开始递归操作 for(int i = nums.size()/2 - 1; i >= 0; i--){ minHeapify(nums, i, nums.size()); } } void heapSort(vector<int>& nums){ initHeap(nums); for(int i = nums.size() - 1; i > 0; i--){ swap(nums[i], nums[0]); // 堆首堆尾互换再调整直至堆大小为1 minHeapify(nums, 0, i); } } -
快速排序?
void quickSort(vector<int> nums, int left, int right){ // 返回枢纽 if(left >= right) return; int pivot = nums[left]; int i=left, j=right; while(i < j){ while(i < j && nums[j] >= nums[i]) --j; nums[i] = nums[j]; while(i < j && nums[i] < nums[j]) ++i; nums[j] = nums[i]; } nums[i] = pivot; quickSort(nums, left, i-1); quickSort(nums, i+1, right); } -
希尔排序(原理):增量每次选择k = n/2, 对子数组进行插入排序


-
计数排序:对一千万个整数排序,整数范围在[-1000,1000]间
- 用来计数的数组C的长度取决于待排序数组中数据的范围(等于待排序数组的最大值与最小值的差加上1),这使得计数排序对于数据范围很大的数组,需要大量时间和内存。
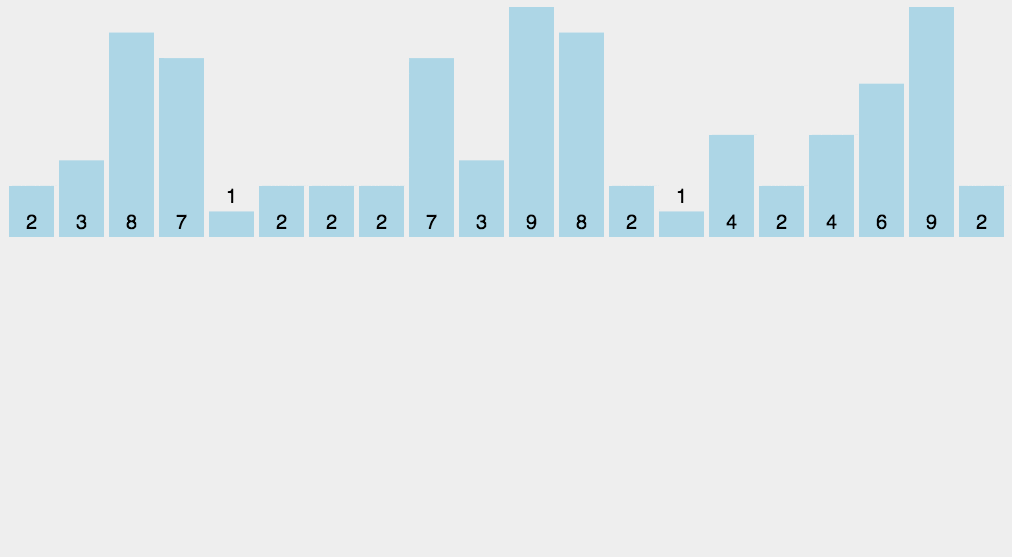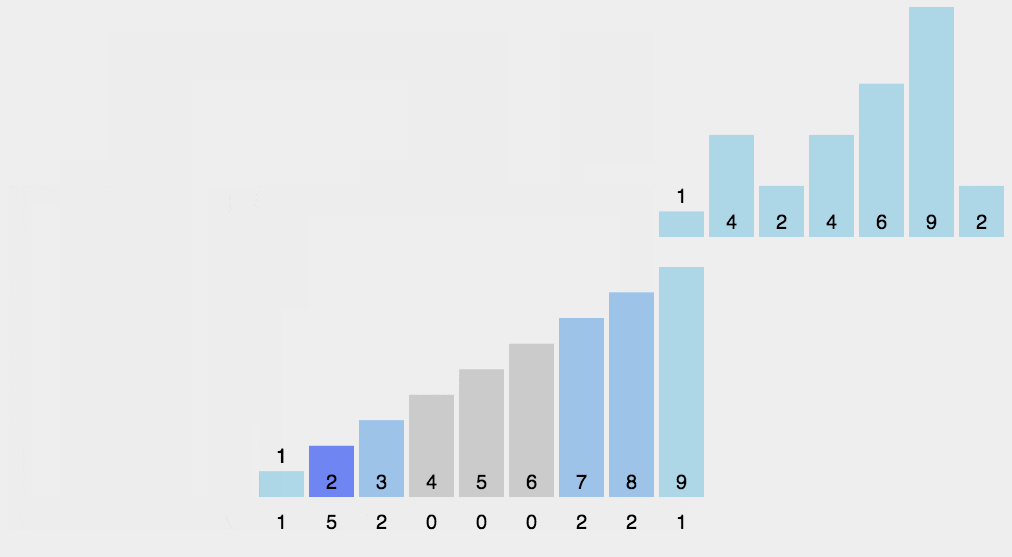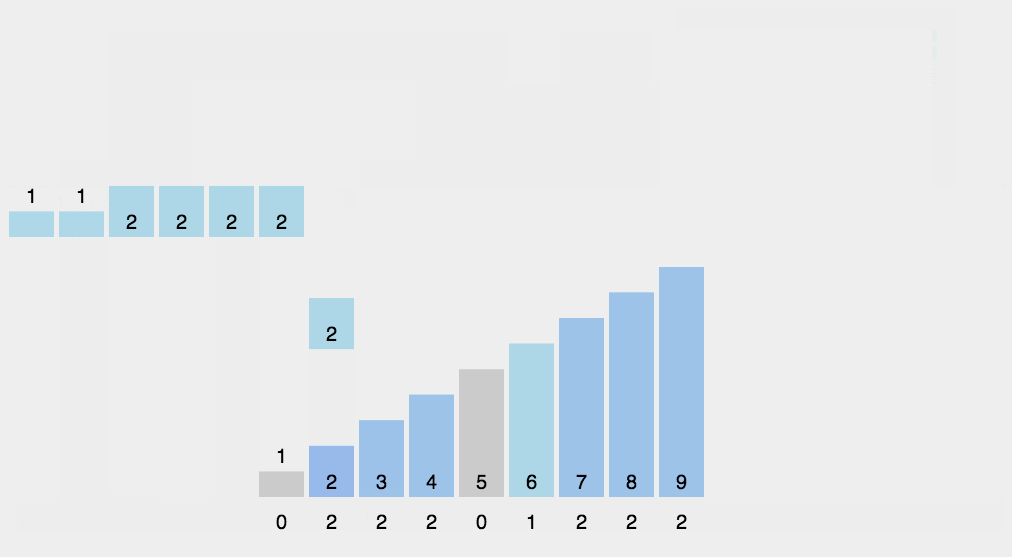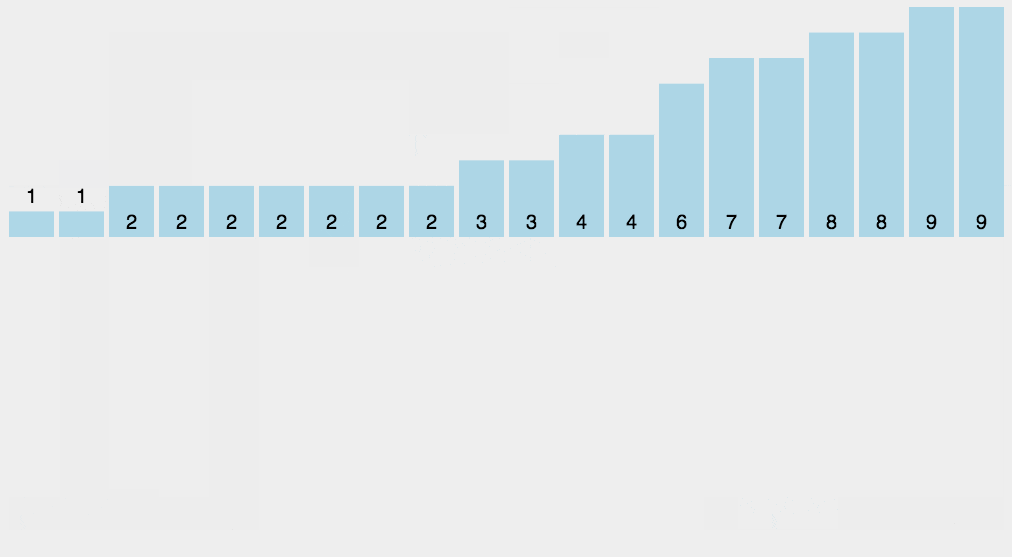
-
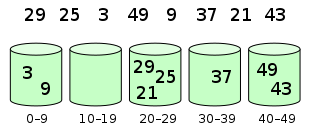
桶排序:是计数排序的升级版
映射函数一般是 f = array[i] / k; k^2 = n; n是所有元素个数
将数组中的数按照映射函数放到对应的桶中,桶内排序,然后再拼接起来
桶中一般使用链表,设置节点结构体;
-
基数排序
按照从低位到高位依次匹配进十个桶中,桶先进先出,可以设置为队列形式:

-
排序算法怎么选择?
数据量规模较小,考虑直接插入或直接选择。当元素分布有序时直接插入将大大减少比较和移动记录的次数,如果不要求稳定性,可以使用直接选择,效率略高于直接插入。
数据量规模中等,选择希尔排序。
数据量规模较大,考虑堆排序(元素分布接近正序或逆序)、快速排序(元素分布随机)和归并排序(稳定性)。
一般不使用冒泡:涉及太多的交换操作耗时
-
LRU算法实现:最近最少使用
常见其他清理缓存(页面置换算法)方式:LFU,最不频繁使用
主要数据结构:
- 双向链表
- map<int, Node*>用来定位到地址
- 虚拟头尾节点
- 队头为最先使用,队尾为最晚使用
- get()要将该元素移至队首
- put()也要放到队首,重复元素直接使用get,非重复元素放到链表头再操作
缓存应该从键映射到值(允许你插入和检索特定键对应的值),并在初始化时指定最大容量。当缓存被填满时,它应该删除最近最少使用的项目。
它应该支持以下操作: 获取数据
get和 写入数据put。获取数据
get(key)- 如果密钥 (key) 存在于缓存中,则获取密钥的值(总是正数),否则返回 -1。
写入数据put(key, value)- 如果密钥不存在,则写入其数据值。当缓存容量达到上限时,它应该在写入新数据之前删除最近最少使用的数据值,从而为新的数据值留出空间。struct DLinkedNode { int key, value; DLinkedNode* prev; DLinkedNode* next; DLinkedNode(): key(0), value(0), prev(nullptr), next(nullptr) {} DLinkedNode(int _key, int _value): key(_key), value(_value), prev(nullptr), next(nullptr) {} }; class LRUCache { private: unordered_map<int, DLinkedNode*> cache; // key-->DlinkedNode* DLinkedNode* head; DLinkedNode* tail; int size; int capacity; public: LRUCache(int capacity) { this->capacity = capacity; head = new DLinkedNode(); tail = new DLinkedNode(); head->next = tail; tail->prev = head; this->size = 0; } void print(){ DLinkedNode* node = head->next; while(node != tail){ cout<<node->key<<" "<<node->value<<" | "; node = node->next; } cout<<"over"<<endl; } int get(int key) { if(cache.find(key) != cache.end()){ auto node = cache[key]; node->prev->next = node->next; node->next->prev = node->prev; node->prev = head; node->next = head->next; head->next = node; node->next->prev = node; return node->value; } return -1; } void put(int key, int value) { int store_value = get(key); if(store_value == -1){ if(this->size == this->capacity){ // delete the last element auto delete_node = tail->prev; delete_node->prev->next = delete_node->next; delete_node->next->prev = delete_node->prev; cache.erase(delete_node->key); delete(delete_node); this->size--; } DLinkedNode* new_node = new DLinkedNode(key, value); new_node->prev = head; new_node->next = head->next; head->next = new_node; new_node->next->prev = new_node; cache[key] = new_node; this->size++; } else if(store_value == value){ return; } else{ cache[key]->value = value; } } }; -
Redis跳表实现:
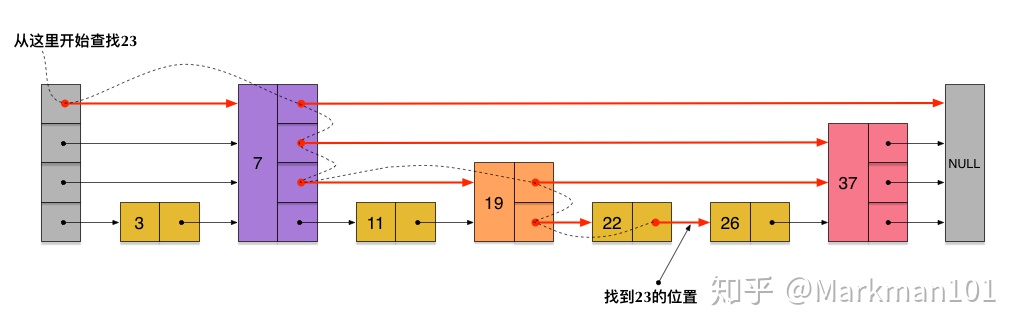
-
接雨水
C++算法题常用技巧
1. C++ lambda表达式:
std::sort(vec.begin(), vec.end(),
[] (const Item& v1, const Item& v2) { return v1.a < v2.a; });
std::for_each(vec.begin(), vec.end(),
[] (const Item& item) { std::cout << item.a << " " << item.b << std::endl; });
[]中填写需要的变量,或者=,&,=表示值传递,&表示引用;
具体细节:C++ Lambda表达式的完整介绍 - 知乎 (zhihu.com)
另外对set / map / priority_queue 自定义排序,可以重写()运算符:
struct intComp {
bool operator() (const int& lhs, const int& rhs) const{
return lhs > rhs;
}
};
set<int, intComp> s1
注意不同的是sort函数中的比较参数传入的是一个函数指针,而容器类的比较参数传入的是类。
priority_queue也可以使用lambda来自定义排序,但定义方式略有不同:
auto myFun = [](int a, int b){
return a < b; // 大根堆, 这与sort的不一样,sort这样是升序排序。因为这里a是父节点,b是子节点,意思是a<b即做交换,所以是 大根堆
};
priority_queue<int, vector<int>, delctype(myFun)> list_heap(myFun);
需传入元素类型,元素载体,以及使用的lambda函数的类型,最后构造函数中还需要传入该lambda函数;
2. string
-
2.0 基本迭代器
begin(),end() -
2.1
push_back(char),append(string) -
2.2
substr(i, length) -
2.3
[],at都可以获取某位置的char -
2.4
back(),front() -
2.5
std::size_t pos = str.find("live"); -
2.6
insert(pos, str); -
2.7
erase(pos, len), erase(it1*, it2*), erase(it*);
3.二分法(面/笔):
3.1 lower_bound:查找大于等于某个数的第一个位置
3.2 upper_bound:查找大于某个数的第一个位置;
int num[6]={1,2,4,7,15,34};
sort(num,num+6); //按从小到大排序
int pos1=lower_bound(num,num+6,7)-num; //返回数组中第一个大于或等于被查数的值
int pos2=upper_bound(num,num+6,7)-num; //返回数组中第一个大于被查数的值
cout<<pos1<<" "<<num[pos1]<<endl;
cout<<pos2<<" "<<num[pos2]<<endl;
sort(num,num+6,cmd); //按从大到小排序
int pos3=lower_bound(num,num+6,7,greater<int>())-num; //返回数组中第一个小于或等于被查数的值
int pos4=upper_bound(num,num+6,7,greater<int>())-num; //返回数组中第一个小于被查数的值
原文链接:https://blog.csdn.net/qq_40160605/article/details/80150252
注:若需要查找小于等于某个数的最后一个位置,使用
upper_bound(num, num+n, x)-num-1;
//手写实现二分法
#include<iostream>
#include<vector>
using namespace std;
int quick1(vector<int>& nums, int left, int right, int target){
//找到第一个大于等于某数的二分法
while(left <= right){
int mid = (left+right) / 2;
if(nums[mid] < target)
left = mid+1;
else{
right = mid-1;
}
}
return left;
}
int quick2(vector<int>& nums, int left, int right, int target){
//找到第一个大于某数的二分法
while(left <= right){
int mid = (left+right) / 2;
if(nums[mid] <= target)
left = mid+1;
else{
right = mid-1;
}
}
return left;
}
int quick3(vector<int>& nums, int left, int right, int target){
//找到最后一个小于等于某数的二分法
while(left <= right){
int mid = (left+right) / 2;
if(nums[mid] > target)
right = mid - 1;
else{
left = mid + 1;
}
}
return right;
}
//总结:如果mid值不满足条件,此时移动的是哪个指针就返回哪个指针,因为如果当left==right
// 但是不满足条件的时候一定是邻接着满足条件的那个值。
int main(){
vector<int> array = {1,2,3,4,4,4,5,6,8,8,9,10};
int ans1 = quick1(array, 0, array.size()-1, 4); //大于等于
int ans2 = quick2(array, 0, array.size()-1, 4); //大于
int ans3 = quick3(array, 0, array.size()-1, 7); //小于等于
return 0;
}
4.位运算(笔)
4.1 异或xor ^
a ^ b = c ==>b ^ c = aa ^ 0 = aa ^ 1 = !aa ^ a = 0
5. 堆的创建与调整(面)
在STL中:priority_queue容器底层使用堆实现
class Solution {
public:
void minHeapify(vector<int>& nums, int idx, int rangeLimit){
int l = 2 * idx + 1 < rangeLimit? 2*idx+1 : idx;
int r = 2 * idx + 2 < rangeLimit? 2*idx+2 : idx;
int minIdx = nums[l] <= nums[r] ? l: r;
if(nums[idx] <= nums[minIdx]) return;
swap(nums[idx], nums[minIdx]);
minHeapify(nums, minIdx, rangeLimit);
}
void initHeap(vector<int>& nums){
for(int i = nums.size()/2 - 1; i >= 0; i--){
minHeapify(nums, i, nums.size());
}
}
void heapSort(vector<int>& nums){
initHeap(nums);
for(int i = nums.size() - 1; i > 0; i--){
swap(nums[i], nums[0]); // 堆首堆尾互换再调整直至堆大小为1
minHeapify(nums, 0, i);
}
}
int findKthLargest(vector<int>& nums, int k) {
heapSort(nums);
return nums[k -1];
}
};
6.快速选择(面/笔)
/*选择第K大的元素*/
class Solution {
int qselect(int l, int r, int k, vector<int> &nums) {
if (l == r) return nums[l];
int x = nums[l], i = l, j = r;
while (i < j) {
while(i < j && nums[j] >= nums[i]) --j;
swap(nums[i], nums[j]);
while(i < j && nums[i] <= nums[j]) ++i;
swap(nums[i], nums[j]);
}
if(k == j) return nums[k];
else if (k < j) return qselect(l, j-1, k, nums);
else return qselect(j + 1, r, k, nums);
}
public:
int findKthLargest(vector<int> nums, int k) {
int n = nums.size();
return qselect(0, n - 1, n - k, nums);
}
};
7. 一个比较有用的用于分割字符串的方法(以空格分割)
#include<iostream>
#include<sstream>
#include<string>
using namespace std;
int main(){
string strin = "I am a student.";
string str;
istringstream in_str(strin);//将strin定义成流类型
while(in_str >> str){//将流输入到str变量中,将以空格分割
cout<<str<<endl;
}
}
/*
I
am
a
student.
*/
8.归并排序(面试):
class Solution {
public:
void merge(vector<int>& nums, int left, int mid, int right, int &ans){
if(left == right)
return;
int i=left, j=mid+1;
int *temp=new int[right-left+1]; //temp数组暂存合并的有序序列
if(temp == nullptr) return;
int k = 0;
while(i <= mid && j<=right){
// if(nums[i] == nums[j]) {
// temp[k++] = nums[i++];
// temp[k++] = nums[j++];
// }
if(nums[i] <= nums[j]){
temp[k++] = nums[i++];
ans += (j-(mid+1));
}
else{
temp[k++] = nums[j++];
}
}
while(i <= mid){
temp[k++] = nums[i++];
ans += (j-(mid+1));
}
while(j <=right){
temp[k++] = nums[j++];
}
k=0;
for(int i=left; i<=right; ++i){
nums[i] = temp[k++];
}
delete []temp;
}
void mergeSort(vector<int>& nums, int low, int high, int &ans){
if(low < high){
int mid = (low+high)/2;
mergeSort(nums, low, mid, ans);
mergeSort(nums, mid+1, high, ans);
merge(nums, low, mid, high, ans);
}
}
int reversePairs(vector<int>& nums) {
int ans = 0;
mergeSort(nums, 0, nums.size()-1, ans);
return ans;
}
};
9.欧拉筛(笔试)
bool isnp[MAXN];
vector<int> primes; // 质数表
void init(int n)
{
for (int i = 2; i <= n; i++)
{
if (!isnp[i])
primes.push_back(i);
for (int p : primes)
{
if (p * i > n)
break;
isnp[p * i] = 1;
if (i % p == 0)
break;
}
}
}
算法学习笔记(17): 素数筛 - 知乎 (zhihu.com)
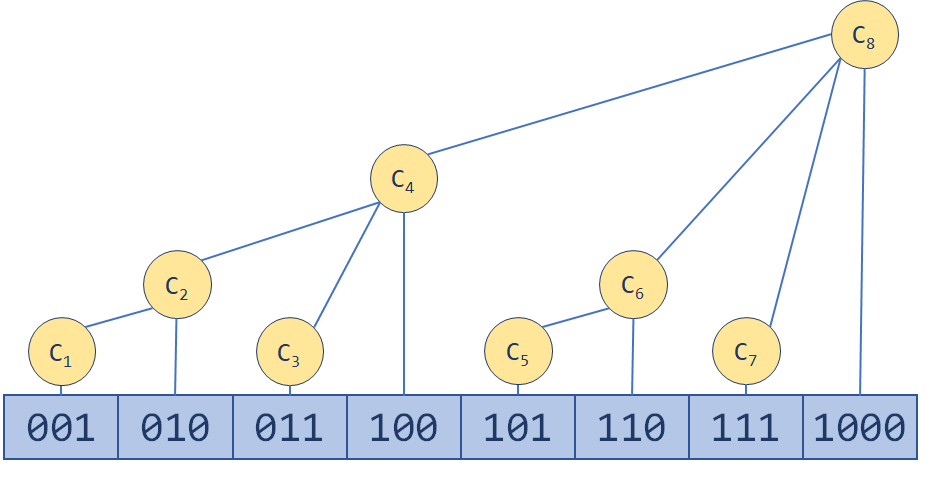
10. 树状数组(笔试)
其中一类查询要求 更新 数组 nums 下标对应的值
另一类查询要求返回数组 nums 中索引 left 和索引 right 之间( 包含 )的nums元素的和。
class NumArray {
private:
vector<int> arr;
vector<int> treefix;
int max_size;
public:
int lowbits(int x){ // 得到最低位1
return x & (-x);
}
NumArray(vector<int>& nums) {
max_size = nums.size();
arr.resize(max_size);
treefix.resize(max_size+1, 0);
for(int i=0; i<max_size; i++){
arr[i] = nums[i];
for(int pos=i+1; pos<=max_size; pos+=lowbits(pos)){
treefix[pos] += arr[i];
}
}
}
void update(int index, int val) {
for(int pos=index+1; pos<=max_size; pos+=lowbits(pos)){
treefix[pos] += (val-arr[index]);
}
arr[index] = val;
}
int prefix(int index){
// 前index项和
int ans = 0;
for(int pos = index+1; pos > 0; pos -= lowbits(pos)){
ans += treefix[pos];
}
return ans;
}
int sumRange(int left, int right) {
// cout<<prefix(left)<<" "<<prefix(right)<<endl;
return prefix(right) - prefix(left-1);
}
};
/**
* Your NumArray object will be instantiated and called as such:
* NumArray* obj = new NumArray(nums);
* obj->update(index,val);
* int param_2 = obj->sumRange(left,right);
*
4 5
1 3 5
001 010 011 100
*/
经典题型
一、单调栈:
对于单调递增栈,可以找到当前要出栈元素的左第一个小于的值(stack.top),与右第一个小于的值(当前要入栈的元素);
接雨水:
84.最大矩形面积:
遍历每一个高度,找到左右边界(e.g. 1 2 3 2 4 1 对于高度2,以2为最低高度,left=0,right=5)
【柱状图中最大的矩形】单调栈入门,使用单调栈快速寻找边界 - 柱状图中最大的矩形 - 力扣(LeetCode)
int largestRectangleArea(vector<int>& heights)
{
int ans = 0;
vector<int> st;
heights.insert(heights.begin(), 0);
heights.push_back(0);
for (int i = 0; i < heights.size(); i++)
{
while (!st.empty() && heights[st.back()] > heights[i])
{
int cur = st.back();
st.pop_back();
int left = st.back() + 1;
int right = i - 1;
ans = max(ans, (right - left + 1) * heights[cur]);
}
st.push_back(i);
}
return ans;
}
85.最大二维矩阵中全一个数(「前缀和 + 单调栈」):
快速幂
int qpow(int n)
{
if (n == 0)
return 1;
else if ((n & 1) == 1)
return qpow(n - 1) * 2 % (long long)(1e9 + 7);
else
{
long long temp = qpow(n>>1);
return temp * temp % (long long)(1e9 + 7);
}
}
int qpow(int a, int n){
int ret = 1;
while(n > 0){
if(n & 1 == 1){
ret *= a;
}
n >>= 1;
a *= a; // 注意是a自乘
}
return ret;
}
// 快速幂求余
int remainder(int x, int a, int p):
int ret = 1;
while (a > 0):
if (a & 1){
ret = (ret * x) % p;
}
x = x * x % p;
a /= 2;
return ret;
数组:
- 数组中第一个只出现一次的数字(只遍历一次数组,使用队列数据结构与哈希表)
- 数组中任意一个重复的数字 (只需哈希表)
- 打印1-最大n位数的全排列(注意避免无前导0,可以先判断当前为第几位再决定遍历的数)
- 调整数组顺序,奇前偶后(快慢指针,头尾指针两种方法)
- 超i过一半的众数(分治法,投票法,快速选择法(但是容易退化成n2复杂度))
- 数组中只有一个数字出现一次,其他均出现两次(异或);
- 数组中只有两个数字出现一次,其他均出现两次(分组异或);
- 和为s的两个数字:对撞双指针;
- 数组中的逆序对个数(归并排序,注意相等的时候应该让i排在前面的指针先走一步)offer 51
动态规划:
-
斐波那契序列:矩阵快速幂,定义矩阵乘法,定义快速幂;
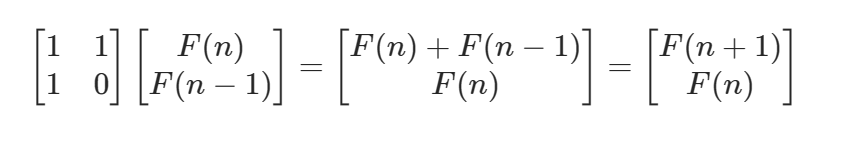
-
第n个丑数(只包含质因子2,3,5):动态规划,三指针。
树形DP:
【动态规划】树形DP完全详解! - Koshkaaa (cnblogs.com)
背包:

图论相关:
-
迪杰斯特拉算法:
-
最小生成树
prim:选择最小的点(稠密图)
kruskal:选择最小的边(并查集)(稀疏图)
-
并查集
-
dfs/bfs
底层手写:
智能指针:
智能指针基本原理,简单实现,常见问题 - 石中火本火 - 博客园 (cnblogs.com)
vector:
需要实现构造函数,析构函数,拷贝构造函数,重载赋值运算符,需要实现函数push_back(),pop_back().使用模板类来实现,包含一个m_first指向第一个元素的位置,m_last指向最后一个元素的位置的后一个位置,m_end指向开辟内存的最后一个位置的下一个位置,m_size表示有多少个元素,m_capacity表示能装多少个元素。