迪杰斯特拉算法

迪杰斯特拉算法（单源最短路径）

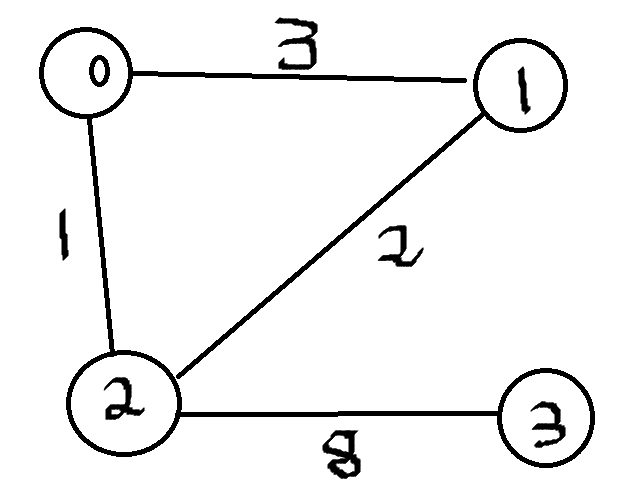
算法基本流程：node 0 as start. 注意算法流程默认图是联通的，若不联通，需要添加循环跳出处理。

step	Node 0	Node 1	Node 2	Node 3	visited point set
0 ( init )	0	INT_MAX	INT_MAX	INT_MAX	{}
1	0 (√)	3	1	INT_MAX	{{0}}
2	0 (√)	3	1 (√)	9	{{0, 2}}
3	0 (√)	3(√)	1 (√)	9	{{0， 2， 1}}
4	0 (√)	3(√)	1 (√)	9(√)	{{0， 2， 1， 3}}

注意步骤是：先找点加入visited set, 再更新距离。

循环次数即为点的个数。

step0：初始化，除了起点本身距离为0，到其余点的距离均为INT_MAX，且目前所有点均未被访问；

step1：找到起点距离最近的点为本身node：0，将node 0加入visited set，，再计算从点0出发的到未访问点的新距离是否可以更小；

如在step2时，新加入了点2，从点2出发查找所有未访问的点{1， 3}，于是发现dis(0-->1) = dis（0-->2) + dis(2-->1) = 3，不更新；

dis(0-->3) = INT_MAX, dis(0-->2) + dis(2-->3) = 9, 后者小于前者，于是更新dis(0-->3) = 9；

以下步骤相同，不再赘述。

伪代码表述：

Init the distance vector as INT_MAX;
Set distance[start]=0;
Init the visited vector as False;

For step in (0, n-1):
	# 每次访问一个点，这个点是距离start最近的点，将其加入现在已经访问的节点集合中
	minP, minD;
	For point in points_all:
		If(point not visited and minD > distance[point]):
			minP = point;
			minD = distance[point];
	# 找到最近的点后，根据这个节点更新目前的可访问距离
	Find point with minium distance in unvisited point set;
	Update distance vector.

实际代码：

#include<iostream>
#include<vector>
#include<set>
#include<algorithm>
using namespace std;
#define M INT_MAX
ostream& operator<<(ostream& os, vector<int>& dis) {

    for(int d : dis){
        os<<d<<" ";
    }
    return os;
}
int main(){
    int n=4; // 节点数量
    vector<int> visited(n, 0); // 访问标记
    vector<vector<int>> map={{0, 3, 1, M},
                             {3, 0, 2, 10},
                             {1, 2, 0, 8},
                             {M, 10, 8, 0},}; // 每两个点之间的距离二维矩阵
    vector<int> distance(n, M);
    int start = 0;
    distance[start] = 0;
    int count = 0;
    while(count++ < n){
        // 找一个距离start最近的未访问点添加到已经访问节点中
        int minPoint, minDis = INT_MAX;
        for(int i=0; i<n; i++){
            if(!visited[i] && minDis > distance[i]){
                minDis = distance[i];
                minPoint = i;
            }
        }
        visited[minPoint] = 1;
        // 更新距离列表
        for(int j=0; j<n; j++){
            if(map[minPoint][j] != INT_MAX && map[minPoint][j] + distance[minPoint] < distance[j]){
                // 这个地方为了防止int溢出，也可以用减号：distance[j]-distance[minPoint] > map[][]
                distance[j] = map[minPoint][j] + distance[minPoint];
            }
        }
    }
    cout<<distance<<endl;
}

此处代码实现其实有些累赘，可以使用unordered_set类型来分别保存已访问的节点和未访问的节点，这样就不必遍历所有的节点了。