杂题分享

计数

P6672 [清华集训2016] 你的生命已如风中残烛

你们这个题啊，很有意思啊。

题意

给你一个长度为 \(m\) 的序列 \(W\) ，其中 \(n\) 个 \(w_i\geq 1\) ，\(\Sigma w_i[w_i\geq 1] =m\) ，拿到一个 \(w_i\) 可以往后拿 \(w_i\) 个数，求在 \(m!\) 中有多少种排列可以拿到第 \(m+1\) 的数。

简化

我们将每个数减一，原问题便转化为给定序列 \(W\) ，其中 \(n\) 个数非负，其余 \(m-n\) 个数均为 \(-1\) ，\(\Sigma w_i=0\) 要求有多少序列满足该序列所有前缀和均非负。

思路

有一个东西，叫作 Raney 引理。

Raney 引理是这么说的：

若存在一个序列 \(A\) ，其中 \(\sum a_i = 1\) ，则其循环移位有且只有一个满足所有的前缀和均为正数。

关于证明：《具体数学》7.5章（机房这本是P301-P302）有关于此的几何方法证明，读者自证不难因此在此口胡一下。

这是一张由序列 \(a=[1,3,-4,1]\) 循环而成的图，直线斜率为 $\frac{1}{4} $ ，定义从无穷小将直线向上平移第一个遇到图像的点为切点。

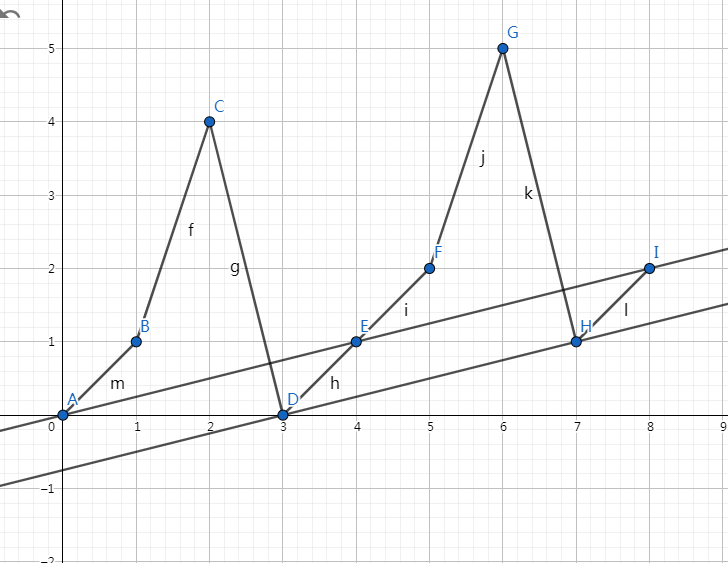
存在性：

根据图像不难发现，若我们从切点开始这个序列，则一定满足前缀和都为正数。

唯一性：

切点一定是该图像每个循环里最小的点之一，且为最靠后的点。

若切点不是最小的点之一都不可能成为切点（根据定义），若非最靠后的最小点（此处我们定义最小为纵坐标最小），则便如图片上经过 \(A(0,0)\) 的直线一样，一定会有点在直线下方，所以到此最小值点的时候前缀和已经小于等于 \(0\) 了。

也许可以感性理解一下

要求所有的数加起来为 \(1\) ，前缀和为正数。思考 \(\frac{1}{n}\) 的意义是什么，可以理解为 \(n\) 个数，平均每个数增长 \(\frac{1}{n}\) ，所以在此直线下面的点等价于到此前缀和小于等于 \(0\) 。

还有一种想法（感谢 Diwanul ， Mr_Avalan ），口胡一下。

现在继续人类智慧。

考虑在 \(m+1\) 处放一个 \(-1\) ，然后将该序列全部取相反数，则该序列就变成了 \(sum_{m+1}=1\) 的形式。

根据 Raney 引理，同一个序列的循环同构只有一个满足条件。

而一个长度为 \(m+1\) 的序列圆排列排列数为 \(m!\) 。

同时由于 \(m+1\) 位是我们固定要求填入 \(-1\) 的位置，由于所有的 \(-1\) 都是等价的，所以我们要消去这些的影响，即除一个 \(-1\) 的数量。

所以最后答案为 \(\frac{m!}{m-n+1}\) 。

ARC125F Tree Degree Subset Sum

给定一棵 \(N\) 个点的树，第 \(i\) 条边连接了 \(A_i\) 和 \(B_i\) 两个节点。求出满足以下条件的数对 \((x,y)\) 的个数：

• \(0≤x≤N\) ；
• 存在一种从树上选出恰好 \(x\) 个节点的方案，使得节点的度数和为 \(y\)。

首先，比较显然的，树的具体形态并不重要，可以直接转化为度数数组，设该数组为 \(d\) ，则 \(d\) 一定满足 \(∑d_i =2n−2,d_i≥1\) （根据 Prufer 序列）。

Prufer 序列

Prufer序列是将一个带标号树和 \(n-2\) 个点值域在 \([1,n]\) 的一个双射，一个有根树与一个 Prufer 序列一一对应。

Prufer 序列有几个性质：

1. 序列长度为 \(2n-2\) ；
2. 每个点编号在序列中出现次数为其在原树中度数减一；
3. 构造完的 Prufer 序列会剩下俩个数（节点），其中一个是 \(n\) 。

那么这道题的限制形式化来讲，就是求有多少个点对，\((x,y)\) ，设取出的点度数为 \(du\) ，满足 \(\sum _{i=1}^x du_i =y\) ，且 \(\sum _{i=1}^n d_i =2n-2\) ， \(d_i>0\) 。

不知道怎么就能很智慧地想到我们不妨将每个 \(d_i\) 减一，则 \(\sum d_i=n-2\) ，\(d_i\geq 0\)，不同的 \(d_i\) 只有不超过 \(\sqrt n\) 种（怎么感觉有语病） ，且一定会存在很多的 0 ，那么我们可以通过调整 \(0\) 的个数选取来调整整体的选取个数。

先摆一个结论：对于同一个 \(y\) ， 能满足条件的 \(x\) 一定构成一个区间。

证明

设对于同一个 \(y\) ，最少的个数为 \(l(x)\) ， 最大的个数为 \(r(x)\) ，\(d_i=0\) 的 \(i\) 个数为 \(z\) 。

显然 \(l(x)\) 里一定不包含 \(d_i=0\) 的节点，则我们可以由 \(l(x)\) 向后延伸至 \(l(x)+z\) ，同理， \(r(x)\) 一定统计了所有 \(d_i=0\) 的节点，则我们可以由 \(r(x)\) 向前延伸至 \(r(x)-z\) 。

因此，需要证明的问题便可以转化为 \(l(x)+z\geq r(x)-z\) ，即 \(r(x)-l(x)\leq 2z\) 。

假设我们选节点的一个点集 \(S\) ，同时设 \(X(S)=\sum_{x\in S} d_x\) ， \(Y(S)=|S|\) ，考虑 \(X(S)-Y(S)\) 的取值。

• \(X(S)\) 取尽可能接近最小值的值，同时 \(Y(S)\) 取尽可能大的值时式子有最小值，那么此时存在 \(\forall d_x ,d_x=0\) ，\(Y(S)=z\) ，则此时 \(X(S)-Y(S)=-z\) 。
• \(X(S)\) 取尽可能接近最大值的值，同时 \(Y(S)\) 取尽可能小的值时式子有最大值，那么此时存在 \(\forall d_x,d_x>0\) ，\(Y(S)=\sum d_x[d_x\geq 1]\) ，则此时 \(X(S)-Y(S)=\sum d_x-\sum d_x[d_x\geq 1]=n-2-(n-z)=z-2\) 。

因此，我们不难得出 \(X(l(x))-Y(l(x))\) 和 \(X(r(x))-Y(r(x))\) 都在 \([-z,z-2]\) 里，更进一步，\(-z\leq X(S)-r(S)\leq X(S)-l(S)\leq z-2\)。

解出来得 \(r(S)-l(S)\leq 2z-2< 2z\) 。

那么我们接下来只要求出 \(l(x)\) 与 \(r(x)\) 就可以力！

考虑DP，由前文所说，不为 \(0\) 的不同 \(d_x\) 不会超过 \(\sqrt n\) 个，我们便不难想到用单调队列优化多重背包。

由于DP式子不难，交给读者自己推着玩，具体可以参考你谷题解区。

还有一种，是用二进制优化，本人太菜，不会，谁会了求你教教我。

用官方题解的话来说： We are done . 我们被干了。

AGC024E Sequence Growing Hard

求有多少个序列组 \(A_0,A_1,⋯ ,A_n\) 满足：

• \(A_i\) 的长度为 \(i\)，且其中元素均为属于 \([1,K]\) 的整数。
• \(A_{i−1}\) 为 \(A_i\) 的子序列。
• \(A_i\) 的字典序大于 \(A_{i-1}\).

这题不难，作为课后思考题吧。

参考题解：https://blog.csdn.net/xmr_pursue_dreams/article/details/103432666

我们可以看成对一个一开始就是空的序列依次插入东西。

特别鸣谢：

• Diwanul ， Mr_Avalan 听我口胡 Raney 引理并帮助我思考，

• 某前数学组学长yzl听我口胡 P6672 ，

• PCQ、lsj帮我理解 Raney 引理和P6672，

• gyq 借我 cy 的《具体数学》，

• ZJK 的课件（虽然有点难懂），

• 各路神仙的题解和博客，

• 以及特别感谢各位在我分享过程中没有一怒之下D死我这个菜鸡stOOOOOOOO。

---

最优化

CF1099F Cookies

题目大意：

两个人玩游戏，一个人可以选择从当前节点走向任意当前节点的儿子节点，另一个人可以选择切断任意一条当前节点与儿子节点的边（也可以选择不切），俩人均用最优策略。

第一个人可以选择在任意自己的回合里结束这个游戏，然后他会原路返回，在返回的时候获取一些价值。

每个节点上有 \(x_i\) 个价值，总价值为 \(x_i\) ，获取价值要花费 \(t_i\) 的时间，节点与其父节点之间要花费 \(l_i\) 的时间，同时要求从根节点到其他节点再返回的总时间不超过 \(T\) 。

求最多能获取多少价值。

显然，二号会剪去原来的最优解，也就是除了根之外，所有节点的最优解都会被剪去。

若没有二号的操作，考虑到在路上的时间是一定的，所以我们尽量吃 \(t_i\) 小的饼干。考虑二分一个时间 \(t\) ，表示所有小于时间 \(t\) 的饼干我们都选了，用树状数组维护这个东西，然后做完了。

• 感谢各位不D之恩。

树与图相关

CF632F Magic Matrix

前面两个限制可以 \(O(n^2)\) 判断。

考虑若满足前俩个限制后该图实际上就是一个无向无自环的完全图。

• 朴素的暴力
  由于 \(a_{i,j}=a_{j,i}\) ，所以限制三可以转化为 \(a_{i,j}\leq \max(a_{i,k},a_{j,k})\) 。我们对于 \(a_{i,j}\) 按权值排序后，检查第 \(i\) 与第 \(j\) 行是否有同时小于 \(a_{i,j}\) 的位置。这个过程是 \(O(n^3)\) 的。只需验证其是否存在，可以用 bitset 加速比较，这样复杂度就除了一个 \(\omega\)，最坏情况大约是 \(5×10^8\)，常数不大，能过。

• 正解
  考虑限制三，\(a_{i,j}\leq \max(a_{i,k},a_{k,j})\leq \max(a_{i,k},\max(a_{k,l},a_{l,j}))=\max(a_{i,k},a_{k,l},a_{l,j})\) ，以此类推，任意选择 \(m\) 和 \(m\) 个 \(k\) ，有 \(a_{i,j}\leq \max(a_{i,k_1},a_{k_1,k_2},a_{k_2,k_3},...,a_{k_m,j})\) 。
  考虑这个式子的意义，不难发现，该式子表示在所有连接 \((i,j)\) 的路径上，最大的边权都大于等于 \(a_{i,j}\) 。反向转化一下，若无法满足这个条件，说明 \((i,j)\) 之间每条边的边权都小于 \(a_{i,j}\) 。
  而这个情况不能存在，因此权值小于 \(a_{i,j}\) 的路径不能使 \((i,j)\) 连通。
  换句话来说， \(a_{i,j}\) 使得 \((i,j)\) 连通，同时还是 \((i,j)\) 上所有路径最大边权中的最小边权，那么 \(a_{i,j}\) 就是最小生成树上的边，然后就做完了。

• 感谢各位不D之恩。

DP优化/博弈论

博弈论是什么？能吃嘛？