网络嵌入

网络表征学习（network representation learning，NRL）&网络嵌入（network embedding，NE）&图嵌入（Graph Embedding Method，GE）：用低维、稠密、实值的向量表示网络中的节点，也即映射到K维的隐空间。

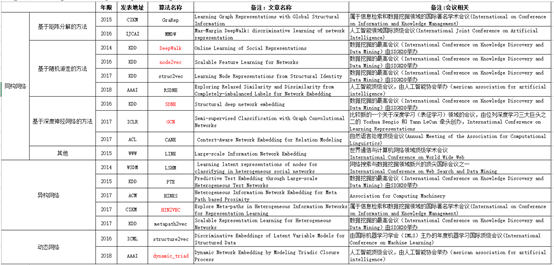
近年来，网络表征学习领域是复杂网络分析方面的研究重点，也是深度学习应用到网络分析的表现之一，几乎每年都有相关的文章发表在KDD、CIKM、IJCAI等数据挖掘和人工智能的顶会，一些比较出名的算法总结如下。

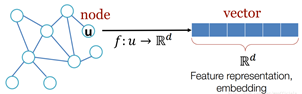
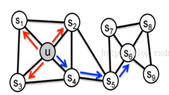
网络表征学习完成后，一方面利于计算存储，传统的方法是使用邻接表存储图，邻接表只记录节点1度邻居的信息，另外，它维度非常高，如果是个完全图你需要n*n的空间复杂度。更重要的是，不用再手动提特征（自适应性），可以将异质信息投影到同一个低维空间中方便进行下游计算，如分类、聚类、半监督学习、标签传播、图分割等等都可以做了，当然其中关键是网络表征的效果（①相似网络结构的节点（structural equivalence）应该需要具有相似的embedding，保存网络拓扑结构，比如u和②属于同质、同一类网络集群的节点（homophily）应该具有相似的embedding比如u和 。

  

一、相关算法

1. deepWalk

这个模型在2014年提出，是这类算法的一个常用baseline模型。借用自然语言处理中的SkipGram的方法进行网络中节点的表征学习，最终目标是学习隐层的权重矩阵即为该网络节点的表征学习。根据SkipGram的思路，最重要的就是定义Context，也就是Neighborhood。​NLP中，Neighborhood是当前Word周围的字，而该方法主要是利用随机游走得到Graph或者Network中节点的Neighborhood，随机游走随机均匀地选取网络节点，并生成固定长度的随机游走序列，将此序列类比为自然语言中的句子（节点序列=句子，序列中的节点=句子中的单词），应用skip-gram模型学习节点的分布式表示。

算法实现步骤：①network/graph ②进行随机游走（random walk）③得到节点序列（representation mapping）④放到skip-gram模型中（中间节点预测上下文节点）⑤output: representation（中间的隐层）

 

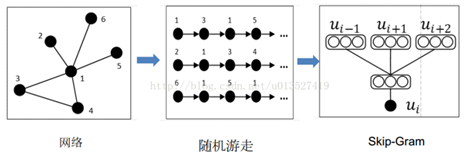
具体skip-Gram模型如下：

skip-Gram是一个简单的三层神经网络，属于自然语言处理word2vec模型之一，给定input word来预测上下文，这里类比就是给定节点u[2]预测邻居节点N(u)，目标函数如下：

 

还是拿文本举例来说明，假设从我们的训练文档中抽取出10000个唯一不重复的单词组成词汇表，我们对这10000个单词进行one-hot编码，得到的每个单词都是一个10000维的向量。其中我们有一个句子“The dog barked at the mailman”。

 

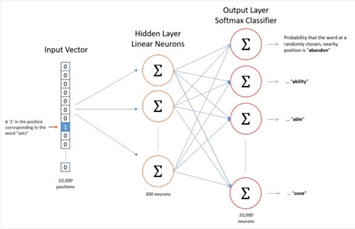
输入层: 假设Input是’dog’， 那么我们输入的就是一个1*10000维向量[0, 1, 0, 0, …0]。如果设置skip_window=2，num_skips=2时，我们将会得到三组 (input word, output word) 形式的训练数据，即 ('dog', 'barked')，('dog', 'the')，('dog', 'at')。input word和output word都是one-hot编码的向量。

隐藏层：隐层没有使用任何激活函数，但是输出层使用了softmax。如果我们想用300个特征来表示一个单词。那么隐层的权重矩阵应该为10000*300（隐层有300个结点）。我们最终需要的是隐层的权重矩阵。

 

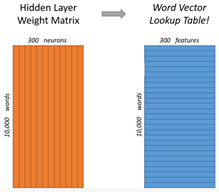
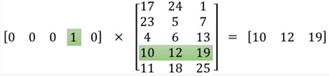
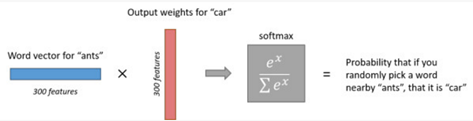
输出层：经过神经网络隐层的计算，dog这个词会从一个1 *10000的向量变成1 *300的向量，再被输入到输出层。输出层是一个softmax回归分类器，它的每个结点将会输出一个0-1之间的概率值（词汇表各单词与InputWord同时出现的概率），这些所有输出层神经元结点的概率之和为1。我们训练是要使得output word输出的概率最大。

2. node2vec

类似于deepwalk，主要的创新点在改进了随机游走的策略，不是以一种固定的模式进行sampling（均匀分布的抽样），利用参数控制随机游走同时考虑到网络的局部（BFS）和宏观的信息（DFS），这样就能同时捕捉节点的结构一致性（structural equivalence）和同质性（homophily）两个特征，具有很高的适应性。

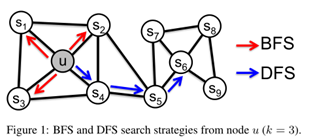
算法实现步骤：①network/graph

②进行随机游走（2nd-order random walks），引入两个超参数p和q，实现参数控制跳转概率的随机游走。

若图E存在边（v, t），当游走到的节点为V，则V将以传递概率 选择下一节点x，其中Z是正则化常数，  ， 是边的权重， 如下图所示， 是节点t和x的最短路径，取值只有{0，1，2}，当下一个节点x就是t时 ，当下一个节点x与节点t和节点v等距时 ，在其他情况 。

-- Return parameter，p，控制重新返回该节点的概率，该值越大（>max（q,1））越不可能采样一个已经经过的节点，反之，该值越小（>min（q,1））越有可能返回原来的节点，即更容易让随机游走变得local，对应于BFS，如图中从t跳到v以后，有1/p的概率在节点v处再跳回到t。

-- In-out parameter，q，控制回溯和离开的概率，如果q>1随机游走会趋向于采样比较近的点，如果q<1随机游走会趋向于采样那些较远的节点，对应于DFS。

 

③得到节点序列（representation mapping）④放到skip-gram模型中（中间节点预测上下文节点）⑤output: representation

3. SDNE

之前的算法都是学习浅层的神经网络，浅层模型往往不能捕获高度非线性的网络结构，为了有效捕捉高度非线性网络结构并保持全局以及局部的结构，作者提出了Structural Deep Network Embedding (SDNE) 方法。论文首次提出了一个半监督的深层模型，它具有多层非线性函数，从而能够捕获到高度非线性的网络结构，通过半监督的深度模型中联合优化一阶相似（两个节点有边，则他们具有正向的一阶近似，否则一阶近似为0）和二阶相似（两个节点的二阶相似性，取决于其邻居节点的相似性 和 ），这样同时保留了局部和全局的网络结构，并且对稀疏网络是robust。

算法框架：

为了捕捉高度非线性的网络结构，论文提出了一种深度架构，它由多个非线性映射函数组成，通过将输入数据映射到高度非线性的潜在空间以捕获网络结构。论文通过重构每个节点的邻域结构来设计无监督学习部分来保持二阶相似性，同时，对于一些成对有边的节点，我们利用它们的一阶相似性作为监督信息来改进embedding。具体细节和损失函数如下：

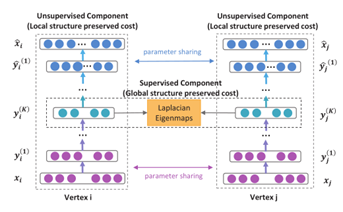
①利用无监督组件autoencoder保持二阶相似性（全局网络结构）。将input X（xi=si）经过多层非线性映射encoder到表示空间，再把表示空间decoder回 。其损失函数定义如下（由于网络的稀疏性对于0项给予更多惩罚）：

 

 

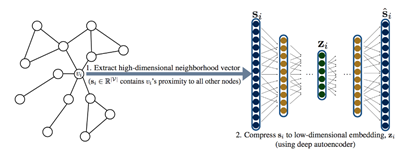
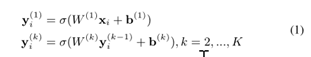
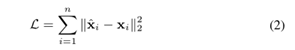
②为了捕捉局部的网络结构，利用有监督的信息（有边连接的节点embedding的相似性）保持一阶相似性。损失函数定义如下：

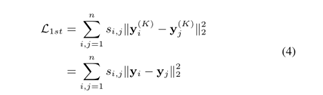
③结合上面监督学习与无监督学习，联合后的最小化目标函数如下，再根据反向传播和SDG就可以计算出隐向量。对于新的节点比如 只需要输入其与现存节点邻接矩阵，就可以用以前的模型进行训练，如果新节点与现存节点没有联系，则无法预测。

 

4. GCN

基于图卷积神经网络的半监督学习，它为图（graph）结构数据的处理提供了一个崭新的思路，将深度学习的神经网络应用到图数据上。它能同时对节点特征信息与结构信息进行端对端学习，运行速度较快，是目前对图数据学习任务的较佳选择，但不适合于有向图，还不能加入边的特征。（基于深度学习的算法最好要在GPU上跑，代码用的tensorflow的框架）

算法框架：

已知图 G =（V，E），其中X表示顶点集V的特征，A表示图的结构信息，通常使用邻接矩阵。在一层的graph conv中，使用上层的输出 ，A和本层的W作为输入，经过某种非线性函数f映射后，便可以得到本层的输出，最后经过一层softmax，可以直接预测。给定一部分标签，可以根据有标签的数据训练该图卷积模型。

 

 

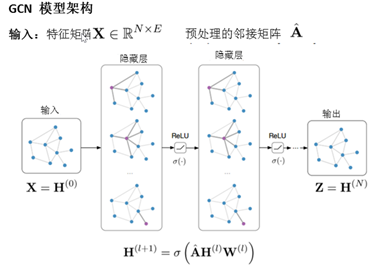
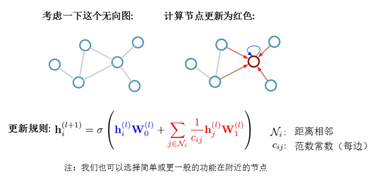
具体的图卷积算子f如下（从光谱图卷积框架开始，做了一些简化，显著加快了训练时间并得到了更高的准确性，定义了在图卷积模型中使用的参数化滤波器filter），即层级之间传播规律，根据邻域进行消息更新，将相邻节点的所有特征矢量相加。其中，W(l) 是第 l层神经网络的权重矩阵，σ() 是一个非线性激活函数如 ReLU ，D是对角线节点次数矩阵。由于A是图的邻接矩阵，所以只有在当前点与其他点有连接的时候才会有值，这样AHW就会表示当前节点的所有邻居在上一层的输出乘以W。这样，我们通过函数σ就仅仅看到了当前点的局部连接。同时，当我们使用多层的graph conv时，H2会利用H1的值，H1利用的是当前节点的1阶邻居的信息，而H2便是利用当前节点1阶和2阶邻居的信息。对称归一化邻接矩阵 是生成的边（ ）的归一化常数（D 是对角节点度矩阵，相当于取相邻节点特征的平均值）

 

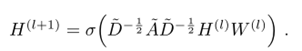
5. HIN2VEC

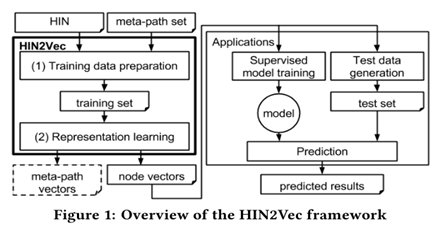
HIN2VEC主要是学习异质信息网络节点和关系的网络表征。该模型属于神经网络模型，通过最大化预测节点之间关系的可能性，同时学习节点和关系的表示向量，这种多任务学习方法能够把不同关系的丰富信息和整体网络结构联合嵌入到节点向量中。

 

元路径（meta-path）：给定一个异构信息网络， ，元路径是节点类型序列a1, a2, …an或者边类型序列r1, r2…rn-1。例如下图3的paper-author HIN里面二度的元路径有R= {P−P,P−A,A−P,P−P−A,P−P−P,P−A−P,A−P−P,A−P−A}

 

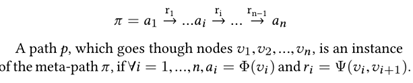
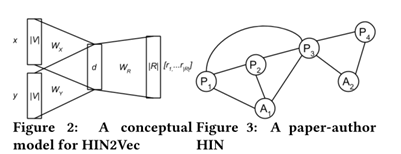
作者最初设想的是构建一个神经网络模型，通过预测任意给定节点对之间的一组目标关系（多分类任务预测）学习节点embedding，如下图2，但这样不仅在训练数据的准备和模型的学习上面都会产生巨大的开销，因为对于一个复杂网络而言，获取网络中两个节点的所有关系是很困难的。最终作者把问题简化为二分类问题，即给定一对节点X、Y和某特定路径r，预测两个节点是否存在该路径关系，这样就可以通过随机游走产生训练数据集，另外参数更新的复杂度也降低了。    

算法实现步骤：①基于随机游走和负采样（在效率和质量之间平衡）生成数据。以上图3的paper-author为例，假设我们产生了随机游走路径P1, P2, A1, P3, A1另外设定目标关系只包含2度以内的元路径，由此对于第一个节点P1我们可以产生训练集<P1, P2, P-P>和<P1, A1, P-P-A>，对于第二个节点P2我们可以产生训练集<P2, A1, P-A>和<P2, A3, P-A-P>，依次类推。上述随机游走只能产生正样本，负样本的产生则需要借助负例采样，随机替换上述正例中的节点，比如把<P1, P2, P-P>中的P2换成P3，更换的必须是同类型的节点（有可能产生正确的，要进行过滤）。

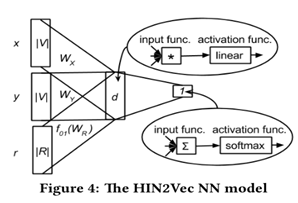
②表示学习。构建神经网络模型，预测是否存在某特定的路径。

输入层：三个one-hot向量 。

隐藏层：经过权重矩阵相乘后得到隐向量 作为输入（r的处理略有不同，因为r表达了不同的含义，通过正则化函数 把隐向量的值约束到了[0,1]），输出为 ，其中 运算，是采用了Hadamard函数。

输出层：输入为 ，也就是对隐含层的d维向量的元素求和。激活函数为sigmoid函数，计算sigmoid( )。

 

最优化目标：训练数据集的形式为<x, y, r, L(x,y,r)>，其中L(x,y,r)是一个二值，代表x和y是否有关系r。通过反向传播(backpropagation)和随机梯度下降(stochastic gradient descent)最优化目标函数O，得到Wx和WR。当L(x,y,r)=1时， 目标是最大化 ，反之，当L(x,y,r)=0时， 目标是最小化 ，因而可以转化成下图中最大化

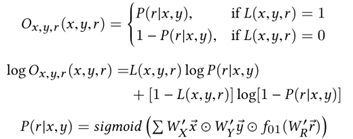
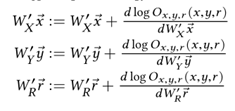
6. dynamic_triad

在真实的世界网络是动态和发展的，作者开发一种新的表征学习算法反应节点之间关系的演进。给定从时间1到时间T序列网络的快照 G1,…GT，我们的目标是学习节点i在每个t时刻的向量表征 。总的来说，dynamic_triad的目标就是模拟三角形闭合的过程，根据不同的节点特性，设计统一的框架定量的衡量开三角发展为闭三角的概率。

 

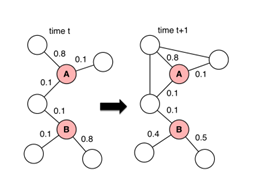
在t时刻有开三角，不认识彼此，但是他们都认识 ，现在 决定在t+1时刻是否会把 互相介绍认识，我们认为这取决于 和 之间的亲密程度（隐空间距离），根据d维隐向量 决定，

 

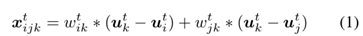
另外，定义社交参数θ，从每个节点隐向量中提取社交信息，因此我们定义t+1时刻（ ）发展为闭三角的概率为，

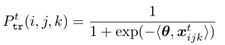
由于 可能有很多共同的好朋友，所以 在t+1时刻发展为朋友的概率，即t+1时刻产生一条新的边 的概率：

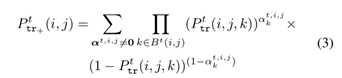
同时，如果他们没有产生边的概率：

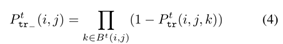
把（3）和（4）结合起来，我们定义三角闭合过程的负对数似然如下，通过最小化损失，求解embedding U。