贝叶斯网络与LDA
一、一些概念
互信息：
两个随机变量x和Y的互信息，定义X, Y的联合分布和独立分布乘积的相对熵。
贝叶斯公式：
贝叶斯带来的思考：
给定某些样本D，在这些样本中计算某结论
出现的概率，即
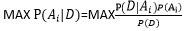给定样本D 所以可以推出
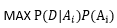，再假定p(Ai)相等，可以推出
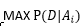，这个就是最大似然估计做的事情，看下取哪个参数
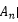的时候，D出现的概率最大，最大似然估计其实假定了任何参数被取到的概率都是一样的。
二、贝叶斯网络
随机变量之间并不是独立，而是存在复杂的网络关系。贝叶斯网络又称为有向无环图模型，是一个概率图模型（PGM），根据概率图的拓扑结构，考察一组随机随机变量{X1,X2…Xn}及其n组条件概率分布的性质。有向无环图中的节点表示随机变量，他们可以是观查到的变量，或隐变量、未知参数等。若两个节点间以一个单向箭头连接在一起，表示两个事件有关系，两节点就会产生一个条件概率值。马尔科夫网络是无向图网络。
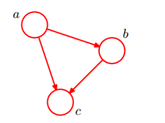
一个简单的贝叶斯网络：
P(a, b, c)=P(c|a, b)P(b|a)P(a)
全连接贝叶斯网络：
每一对结点之间都有边连接，比如有5个结点就有=10条边。其实这种是我们最不希望看到的，因为这样建立的模型比较复杂。
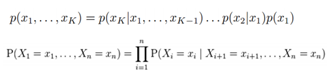
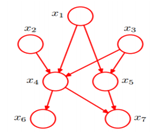
一个正常的贝叶斯网络：
有些边缺失，直观上X1和X2独立，X6和X7在X4给定的条件下独立。
X1，X2…X7的联合分布：
P(x1) P(x2) P(x3) P(x4|x1,x2,x3) P(x5|x1,x3) P(x6|x4) P(x7|x4,x5)
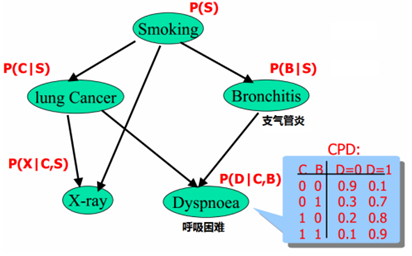
一个实际贝叶斯网络：
需要知道的参数个数为1+2+2+4+4=13 和全连接的2**5=32个相比少了一半。根据实际情况建立贝叶斯网络，可以减少大量参数。有可能实际中是知道一个人是否抽烟，知道x-ray和呼吸困难的情况，从而可以推断得肺癌和支气管炎的概率。
贝叶斯网络的形式化定义：
特殊的贝叶斯网络：
结点形成一条链式网络，称作马尔科夫模型。Ai+1只有Ai有关。有二阶马尔科夫网络、三阶马尔科夫网络，但我们往往不会去做那么高阶的马尔科夫网络，太复杂了。PLSA主题模型属于马尔科夫网络。
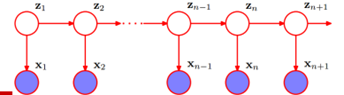
HMM:
假定z1、z2….zn+1（文字）是隐状态的，我们观察到的是x1、x2…xn+1（人说话的波形数据）
贝叶斯网络用处：
诊断：P（病因|症状）
预测：P（症状|病因）
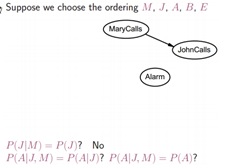
贝叶斯网络的构建：
根据独立的条件，一条边一条边的试验，看是否能够连接。此过程可能中看不一定中用。如果有先验的知识，最好先按先验的知识建立贝叶斯网络。
混合网络（离散+连续）的构建：
隐马尔可夫里面就是混合网络。LDA是贝叶斯网络，都是离散的。
假设cost是服从正太分布的，当subsidy=true的时候有一个ath+bt的均值和方差，当subsidy=false的时候又有另一个ah+b的均值和方差。
然后buys是离散，cost是连续，那么又可以用逻辑回归建模。
三、LDA主题模型
理解篇
复杂的贝叶斯网络是LDA主题模型，是一种无监督的贝叶斯模型。
是一种主题模型，它可以将文档集中每篇文章的主题按照概率分布形式给出，同时它是一种无监督学习的算法，不需要手工标注训练集，仅需要文档以及指定主题的数量k。
是一个典型的词袋模型，即它认为一篇文档是由一组词构成的一个集合，词与词之间没有顺序以及先后关系，一篇文档可以包含多个主题，文档中每一个词都由其中的一个主题生成。
超参（参数的参数）
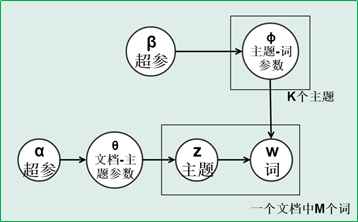
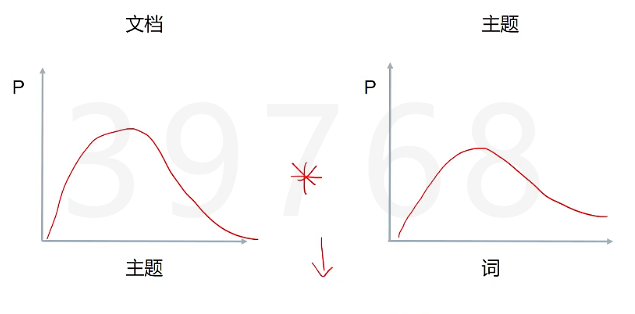
P（单词|文档）= P（单词|主题）*P（主题|文档）
在LDA中我们要判断出两个概率分布，在同一个主题下出现某个词的概率，在同一个文档下属于某个主题的概率，这两个概率的乘积可以让我们印证，在同一个文档下出现某个词的概率，这个是我们可以算出来的，也就是说可以调整这两个分布（先随机设定一个分布），直到P（单词|文档）更符合实际情况（更加拟合）。一篇文章如果属于某个主题，它的用词肯定是有规律的，要求的实际上是P（主题|文档）。
LDA生成过程：
1.对于每篇文档，从主题分布中抽取一个主题
2.从上述被抽到的主题所对应的单词分布中抽取一个单词
3.重复上述过程直到遍历文档中的每个单词
LDA学习过程：
公式篇
正经理解LDA，分为以下五个部分：
1.一个函数：gamma函数
2.四个分布：二项分布、多项分布、beta分布、Dirichlet分布
3.一个概念和一个理念：共轭先验和贝叶斯框架
4.一个采样：Gibbs采样
共轭分布（先验概率和后验概率有同一函数形式，为什么需要共轭分布，为了计算简便，减少我们计算量）
gamma函数 阶乘函数在实数上的推广
二项分布 从伯努利分布（1次）中推出，重复N次，概率密度函数如下
多项分布 是二项分布扩展到多维 单次实验中随机变量取值不再是0-1，而是有多种离散可能值，概率密度函数如下
beta分布，二项分布的共轭先验分布
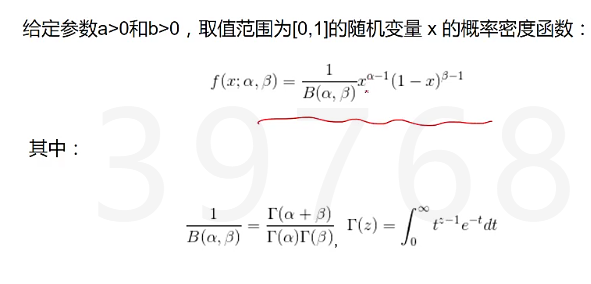
Dirchlet分布 是beta分布在高维上的推广
贝叶斯学派的思考方式： 先验分布π（θ）+样本信息X ===>后验分布π（θ|X）与频率学派的想法不同，不认为要试验很多次，只要知道先验的知识，根据部分样本就可以估计后验分布。
几个主题模型：
Unigram model（最基础的一个文档分类模型）
Mixture of unigrams model（多加了一个分布，通过中间量的主题的分布，来求出文档生成的概率）
该模型的生成过程是：给某个文档先选择一个主题z（引入了一个中间量，通过这个中间量，把两个我们容易观测的东西算出来之后，再观测另外一个我们容易得出的值），再根据该主题生成文档，该文档中的所有词都来自同一主题。假设主题有z1,z2,z3,..zk，生成文档的概率为：
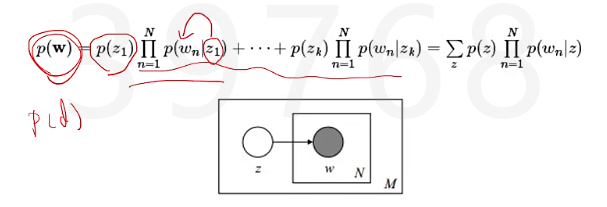
PLSA（比上面Mixture多了 出现几率不一样 的情况）
Mixture of unigrams模型里面，一篇文章只给一个主题，但现实生活中，一篇文章可能多个主题，只不过出现几率不一样。下图中，可以想象成丢塞子，先丢出了主题，再根据主题丢出了单词，第一个就是文档主题分布，第二个就是主题单词分布。
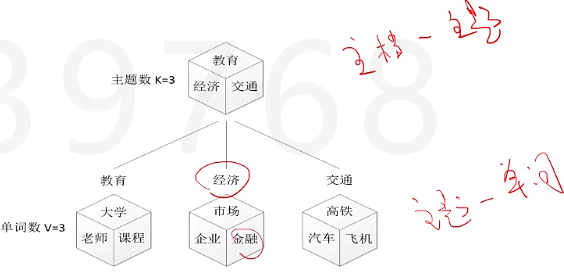
我们的文本生成模型就是如下图
我们通过观测，得到了[知道主题是什么，我就用什么单词]的文本生成模型，那么根据贝叶斯定律，我们就可以反过来推出[看见用了什么单词，我就知道主题是什么]
LDA模型（概率的选择不是先验确定，而是服从狄利克雷分布）
LDA模型就是在pLSA的基础上加层贝叶斯框架，即LDA就是pLSA的贝叶斯版本。第二步中主题分布不是随机选一个确定的概率，而是服从狄利克雷分布，另外从主题中取词也满足狄利克雷分布，也就是在pLSA的基础上加了两层狄利克雷分布。这样又承认了一个随机的可能性在里面，可以让我们这样一个分布不至于因为我们先验的值导致过拟合的状况。pLSA跟LDA的本质区别在于它们估计未知参数所采用的思想不同，前者用的频率派思想，后者用的贝叶斯派思想。
代码：
如果是中文的话，要先分词，转化为Gensim认识的语料库形式，[[一，条，邮件，在，这里],[另，一条，邮件，在，这里]]
from gensim import corpora, models, similarities import gensim #去除停用词 中文的话可以搜索中文虚词列表 stoplist=['very', 'am', 'is', the', 'doesn' texts = [[word for word in doc.lower().split() if word not in stoplist] for doc in doclist]] #建立语料库 #标记化，把每个单词用一个数字index指代，并把我们的原文本变成一条长长的数组 dictionary = corpora.Dictionary(texts) corpus = [dictionary.doc2bow(text) for text in texts] #里面第一个词代表第几个单词，第二个代表这个单词出现几次 #建立模型 lda = gensim.models.ldamodel.LdaModel(corpus=corpus, id2word=dictionary, num_topics=20) #我们可以看到，第10号分类，其中最常出现的单词是： lda.print_topic(10, topn=5) #我们把所有的主题打印出来看看 lda.print_topics(num_topics=20, num_words=5) #两个方法，我们可以把新鲜的文本/单词，分类成20个主题中的一个 #但是注意，我们这里的文本和单词，都必须得经过同样步骤的文本预处理+词袋化，也就是说，变成数字表示每个单词的形式。 lda.get_document_topics(bow) lda.get_term_topics(word_id)
