金融交易图嵌入

之前有段时间关注过图嵌入相关算法，后面又停止关注了，今天偶然看到一篇文章关于图在金融交易场景下的应用，想着那就花时间好好看下吧。

论文链接如下：https://arxiv.org/pdf/1907.07225.pdf 

第一部分 概要

金融交易可以看做是异构图中，交易实体之间的边。在金融场景中，这样的交易图是非常大的（百万或者千万级别的边），并且很稀疏。将机器学习应用到很大很稀疏的图上是很有挑战的。图表示学习可以将节点嵌入到向量空间，而图的拓扑结构在转换后得到保留。在这篇文章中，我们提出了一个新的表示学习方法，应用于信用卡交易的二部图，以学习账户和商家实体的嵌入。并可以将这些嵌入的结果应用于下游的机器学习任务，如欺诈检测。

比较出名的就是GCN、node2vec等将稀疏图矩阵嵌入到低维空间（保证几何相似性，类似的图形子结构在图嵌入空间相同位置）

这篇文章主要聚焦于大规模的信用卡交易数据，聚焦于账户持有者和商家之间的隐式二部图。基于这些交易的编码可以体现消费模式，地理位置和商户行业/类别

 

第二部分 历史研究

图嵌入技术的类型。

同构网络。最大的挑战在于通过可行的计算方式编码节点的领域拓扑结构。隐向量需要保存不同节点的临近相似性和结构相似性，程度不一样，隐向量的表达不一样。

异构网络（不同类型的节点或辅助图信息）。异构网络的问题主要是通过metapath2vec解决。metapath定义实体类型，随机游走产生和这些元路径一致的schema。这个方法之后得到了扩展，包含了节点和边的属性来增强表示学习。

这些works里面节点嵌入的估计都是采用的典型抽样的方法。

] Y. Cen, X. Zou, J. Zhang, H. Yang, J. Zhou, and J. Tang, “Representation learning for attributed multiplex heterogeneous network,” 2019. 

W. L. Hamilton, R. Ying, and J. Leskovec, “Inductive representation learning on large graphs,” CoRR, vol. abs/1706.02216, 2017. [Online]. Available: http://arxiv.org/abs/1706.02216 

图嵌入的应用场景。

 主要应用于在线推荐。有用autoencoder做账户交易数据嵌入的。本文是图嵌入在金融领域的第一次应用。

 

第三部分 方法

A异构图projection

在本文的数据属于二分图。所以元路径主要是如{Account, Merchant, Account}、{Merchant, Account,Merchant}，我们只会考虑遵循这些三元组的graph walk，认为在相同商户消费的account相似。另外，我们可以获取相似的训练集从原来的二分图中引入两个同构映射图：Account图和Merchant图。在同构图上进行randomwalk。这种方法带来了计算收益和增强了灵活性。下面主要是介绍Merchant 的embedding。

B预处理阶段：以交易对的形式modeling graph

两个Merchant之间有边的情况，是在给定的时间窗口内至少有一个account在两个Merchant都交易过。在给定时间内交易的越频繁权重越大，如下图（a）所示，把交易数据，按照这个规则转换为交易对Transaction Pairs。

时间窗口的选取，取决于我们关注的节点类型，以及图密度。例如如果我们更关注的是在相同商家交易的相似账户而不是同一账户交易的不同商户有哪些，那我们的窗口尽可能选短一点，这样能保证在较短时间内的商户都是比较相关的。通过这种策略，可以获取给定时间窗口策略内所有交易数据的商户图，而不是通过在每个商户的随机游走。

a 使用品牌名水平的Merchants name而不是raw name。去掉每天交易量小于50的稀有商户。

b 把线上商户和实体商户分离。

c 近似deepwalk。对于金融交易图来说，一跳和两跳社区就足够了产生有效的嵌入。可以选取比较小的walk length 和 比较短的context window。使用负采样。

 

 

 

目标函数看出可以捕获一阶相似性关系

第四部分 结果

欺诈检测的应用

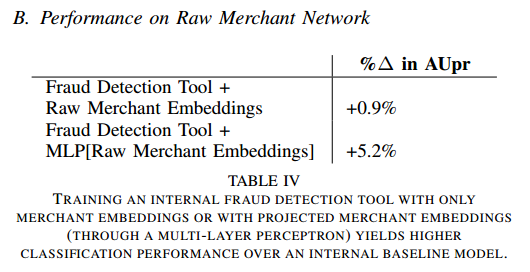
 作为额外的特征加入模型，提高了大约1%。但这种方式会对特征空间的维度又提升了，为此添加了一个MLP，作为嵌入的输入交易的商家并预测是否欺诈。然后再把这个预测的欺诈概率作为输入，直接提高了5.2%。