Java位运算原理及使用讲解
前言
日常开发中位运算不是很常用,但是巧妙的使用位运算可以大量减少运行开销,优化算法。举个例子,翻转操作比较常见,比如初始值为1,操作一次变为0,再操作一次变为1。可能的做法是使用三木运算符,判断原始值为1还是0,如果是1,设置为0,否则设置为0.但是使用位运算,不用判断原始值,直接改变值就可以:
1^num//num为原始值
当然,一条语句可能对代码没什么影响,但是在高重复,大数据量的情况下将会节省很多开销。
以下是自己整理的关于java位运算的部分内容,如有错误,还请指出,以共同进步,先行致谢。
1. 位运算符
1.1 java支持的位运算符:
&:按位与。
|:按位或。
~:按位非。
^:按位异或。
<<:左位移运算符。
>>:右位移运算符。
<<<:无符号右移运算符。
位运 算 符 中 ,除 ~ 以 外 ,其余 均 为 二 元 运 算 符 。 操 作 数 只 能 为 整 型 和字 符 型 数 据 。
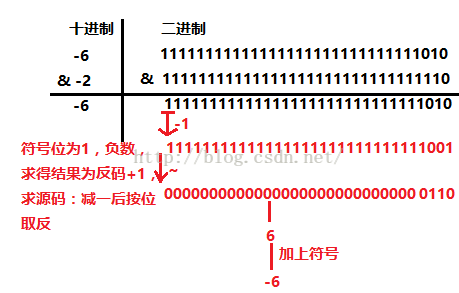
Java使用 补 码 来 表 示 二 进 制 数 ,在补 码 表 示 中 ,最高 位 为 符号 位 ,正数 的 符 号 位 为 0,负数 为 1。补 码 的 规 定 如 下 :
对 正 数 来 说 ,最高位为 0,其余 各 位 代 表 数 值 本 身 (以二 进制 表 示 ),如 +42的补码 为 00101010。
对 负 数 而 言 ,把该 数 绝 对 值 的 补 码 按 位 取 反 ,然后 对 整 个数 加 1,即得 该 数的 补 码 。 如 -1的补 码 为11111111111111111111111111111111(00000000000000000000000000000001按 位 取 反 11111111111111111111111111111110+1=11111111111111111111111111111111 )。为何有那么多0、1,java中int是32位的。
1.2 按位与(&)
按位与的运算规则
|
操作数1 |
0 |
0 |
1 |
1 |
|
操作数2 |
0 |
1 |
0 |
1 |
|
按位与 |
0 |
0 |
0 |
1 |
规则总结:只有两个操作数对应位同为1时,结果为1,其余全为0. (或者是只要有一个操作数为0,结果就为0)。
举例:
1.3 按位或(|)
按位或的运算规则
|
操作数1 |
0 |
0 |
1 |
1 |
|
操作数2 |
0 |
1 |
0 |
1 |
|
按位或 |
0 |
1 |
1 |
1 |
规则总结:只有两个操作数对应位同为0时,结果为0,其余全为1.(或者是只要有一个操作数为1,结果就为1)。
1.4按位非(~)
按位非的运算规则
|
操作数 |
0 |
1 |
|
按位或 |
1 |
0 |
在求负数的源码中使用过。
1.5 按位异或(^)
按位异或的运算规则
|
操作数1 |
0 |
0 |
1 |
1 |
|
操作数2 |
0 |
1 |
0 |
1 |
|
按位异或 |
0 |
1 |
1 |
0 |
规则总结:异:1.
1.6 左位移(<<)
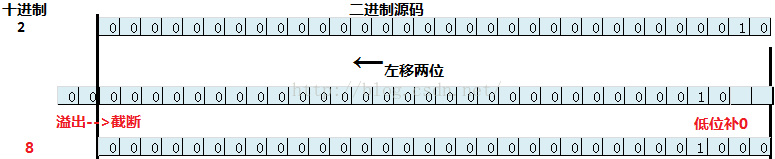
算术右移(>>): 符号位不变,低位补0。如:2<<2结果为8。
当移动的位数超过数字本身的位数时,那么不就都需要补0操作,实际上不是的,java不可能做那么浪费资源的事情。在真正执行位移前,其对要移动的位数做了一些预处理,比如32处理为0,-1处理为31.
1.7 右位移(>>)
低位溢出,符号位不变,并用符号位补溢出的高位。如:-6>>2结果为-2。
1.8 无符号右移(>>>)
低位溢出,高位补0。注意,无符号右移(>>>)中的符号位(最高位)也跟着变,无符号的意思是将符号位当作数字位看待。如:-1>>>1结果为2147483647。这个数字应该比较熟悉,看两个输出语句就知道是什么了:
System.out.println(Integer.toBinaryString(-1>>>1));
System.out.println(Integer.toBinaryString(Integer.MAX_VALUE));
输出结果为:
1111111111111111111111111111111
1111111111111111111111111111111
-1>>>1竟然得到了int所能表示的最大整数,精彩。
除了使用-1>>>1能得到Integer.MAX_VALUE,以下的也能得到同样的结果:
//maxInt
System.out.println(~(1 << 31));
System.out.println((1 << -1)-1);
System.out.println(~(1 << -1));
使用位运算往往能很巧妙的实现某些算法完成一些复杂的功能。
常见使用
1. m*2^n
可以使用m<<n求得结果,如:
System.out.println("2^3=" + (1<<3));//2^3=8
System.out.println("3*2^3=" + (3<<3));//3*2^3=24
计算结果是不是很正确呢?如果非要说2<<-1为什么不等于0.5,前面说过,位运算的操作数只能是整型和字符型。在求int所能表示的最小值时,可以使用
//minInt
System.out.println(1 << 31);
System.out.println(1 << -1);
可以发现左移31位和-1位所得的结果是一样的,同理,左移30位和左移-2所得的结果也是一样的。移动一个负数位,是不是等同于右移该负数的绝对值位呢?输出一下就能发现不是的。java中int所能表示的最大数值是31位,加上符号位共32位。在这里可以有这样的位移法则:
法则一:任何数左移(右移)32的倍数位等于该数本身。
法则二:在位移运算m<<n的计算中,若n为正数,则实际移动的位数为n%32,若n为负数,则实际移动的位数为(32+n%32),右移,同理。
左移是乘以2的幂,对应着右移则是除以2的幂。
2. 判断一个数n的奇偶性
n&1 == 1?”奇数”:”偶数”
为什么与1能判断奇偶?所谓的二进制就是满2进1,那么好了,偶数的最低位肯定是0(恰好满2,对不对?),同理,奇数的最低位肯定是1.int类型的1,前31位都是0,无论是1&0还是0&0结果都是0,那么有区别的就是1的最低位上的1了,若n的二进制最低位是1(奇数)与上1,结果为1,反则结果为0.
3. 不用临时变量交换两个数
在int[]数组首尾互换中,是不看到过这样的代码:
-
public static int[] reverse(int[] nums){ -
int i = 0; -
int j = nums.length-1; -
while(j>i){ -
nums[i]= nums[i]^nums[j]; -
nums[j] = nums[j]^nums[i]; -
nums[i] = nums[i]^nums[j]; -
j--; -
i++; -
} -
return nums; -
}
连续三次使用异或,并没有临时变量就完成了两个数字交换,怎么实现的呢?
上面的计算主要遵循了一个计算公式:b^(a^b)=a。
我们可以对以上公式做如下的推导:
任何数异或本身结果为0.且有定理a^b=b^a。异或是一个无顺序的运算符,则b^a^b=b^b^a,结果为0^a。
再次列出异或的计算表:
|
操作数1 |
0 |
0 |
1 |
1 |
|
操作数2 |
0 |
1 |
0 |
1 |
|
按位异或 |
0 |
1 |
1 |
0 |
可以发现,异或0具有保持的特点,而异或1具有翻转的特点。使用这些特点可以进行取数的操作。
那么0^a,使用异或0具有保持的特点,最终结果就是a。
其实java中的异或运算法则完全遵守数学中的计算法则:
① a ^ a =0
② a ^ b =b ^ a
③ a ^b ^ c = a ^ (b ^ c) = (a ^ b) ^ c;
④ d = a ^b ^ c 可以推出 a = d ^ b ^ c.
⑤ a ^ b ^a = b.
4. 取绝对值
(a^(a>>31))-(a>>31)
先整理一下使用位运算取绝对值的思路:若a为正数,则不变,需要用异或0保持的特点;若a为负数,则其补码为源码翻转每一位后+1,先求其源码,补码-1后再翻转每一位,此时需要使用异或1具有翻转的特点。
任何正数右移31后只剩符号位0,最终结果为0,任何负数右移31后也只剩符号位1,溢出的31位截断,空出的31位补符号位1,最终结果为-1.右移31操作可以取得任何整数的符号位。
那么综合上面的步骤,可得到公式。a>>31取得a的符号,若a为正数,a>>31等于0,a^0=a,不变;若a为负数,a>>31等于-1 ,a^-1翻转每一位.







 浙公网安备 33010602011771号
浙公网安备 33010602011771号