上一节(也就是在四中)我们谈了在经典概率框架下,采用两种方法估算p(t|ci),得出的结论是这两种方法对最后准确率没有显著影响。下面我们在给出一个菜鸟的naiva概率框架。
该框架用概率归一化词袋子中所有词在训练文档集中出现的情况。即p(t)由词袋子模型中的统计信息直接归一化计算,并假设P(C1)=P(c2)=1/2 P(C|t)也直接计算。
比如词袋子中有三个词 {[家务: class1:(1,3)(2,1) class2:(4,1)][俄罗斯: class2:(2,3),(4,1),(5,1)][健康: class1:(2,4),(3,2)]}
那么p(t=家务)=(3+1+1)/[(3+1+1)+(3+1+1)+(2+4)]
注意:(四)中的经典概率模型求p(t)是通过p(t|c)计算的,它认为只有p(t|c)可以通过当前语料库直接得出,其他的概率都要通过此概率推导得出.
在我们的假设中p(c|t)也直接计算。再举个例子p(class=class1|t=“家务”)=(3+1)/(3+1+1)
那么我这个菜鸟这么假设的概率模型合理吗? 会不会导致准确率降低。那么请实验结果来说话吧。
同样我们根据是否计算词在文章中出现的重数,又分为两个情况。
情况一不考率重数;情况二,考虑重数。(上边为情况一的实验结果,下边为情况二的结果)
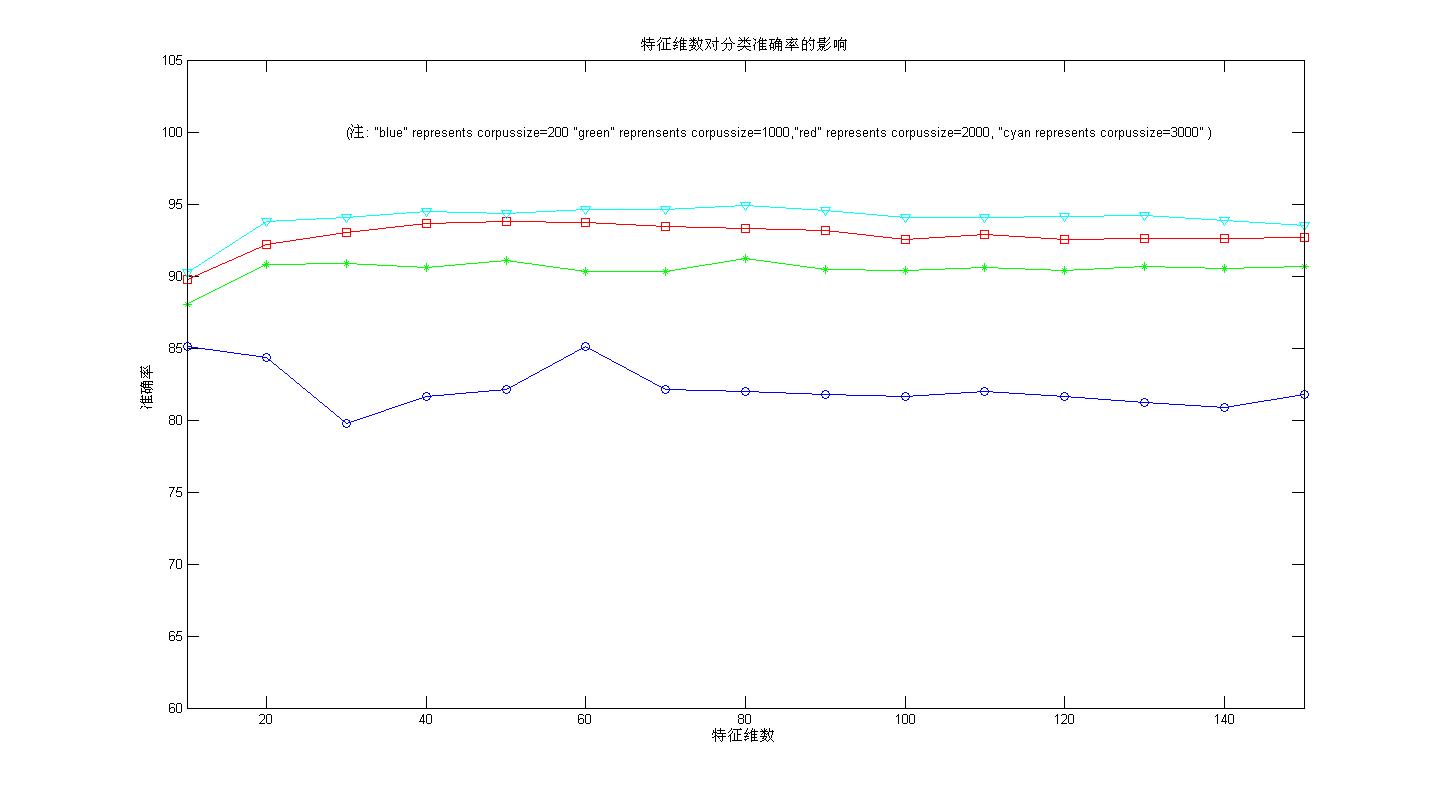
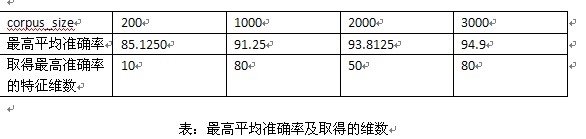
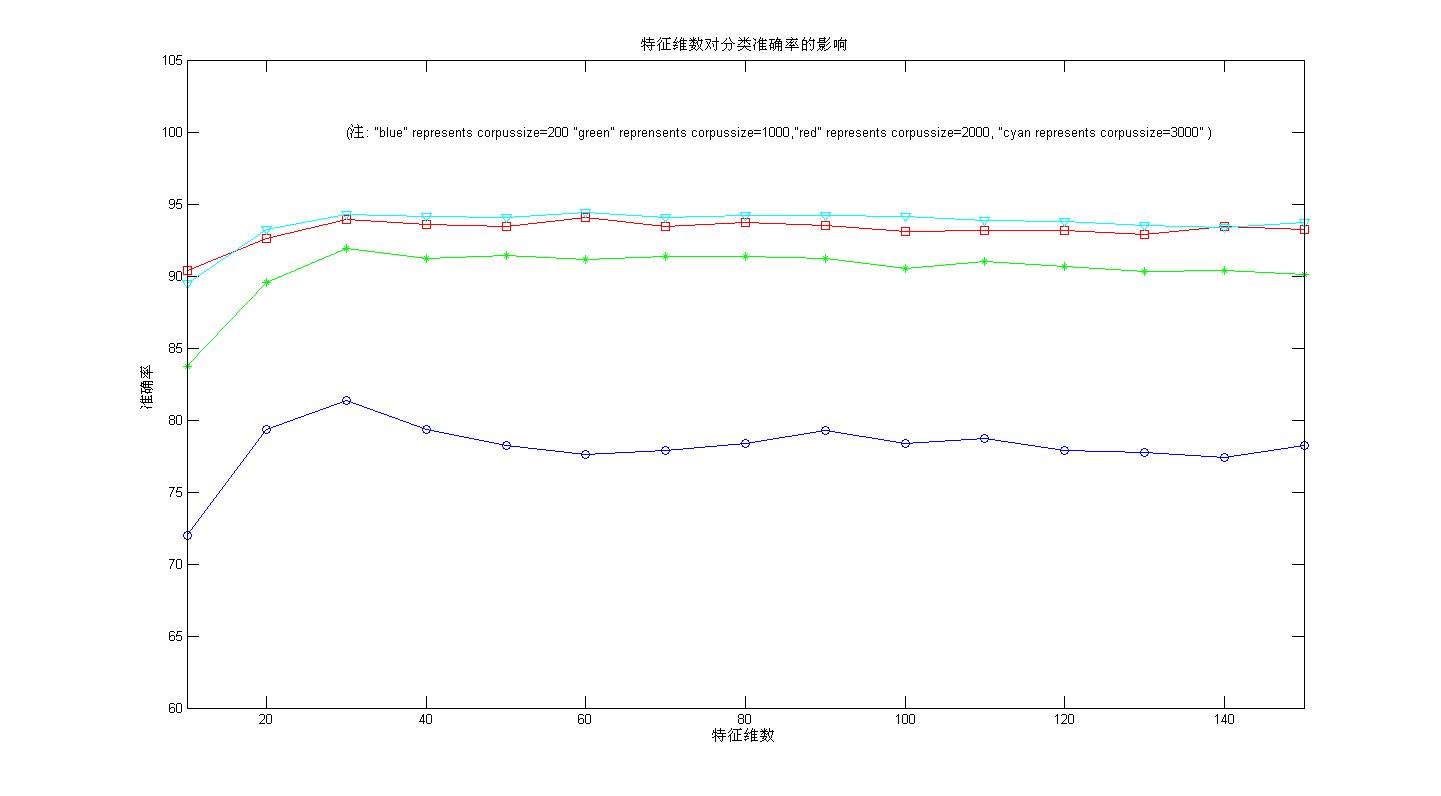
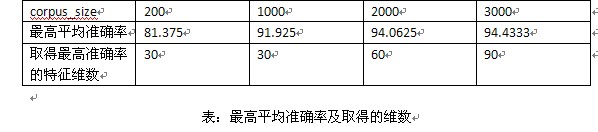
种概率框架下,从最后的实验结果(平均准确率)来看,和论文,教科书上的经典概率框架相比没有明显的不足,我在二元词图+Viterbi算法的中文分词这一系列文章中也提到过,我采用了两种概率估算模式估算概率,但是最后的结果相差不大(在分词中采用的是F值,貌似变化只是千分位的差距如从91.001%变成了91.002%)。另外,在洞庭散人的朴素贝叶斯分类中计算条件概率有这样一段代码

他采用的是不计文章重数的计算概率的方法,Nxc是说x在c类别中的出现的文章数目,Nc是该类别的文章总数,很明显,这种概率的计算方式是错误的!!照他这么算,P(x1||c)+p(x2|c)+....+p(xn|c)!=1(n为词典中的总词数)。原因在于:很多词可以同时出现在一篇文章中。但是他的这种计算方法并不会影响到最后的分类准确率。我在做实验的时候,特意采用了他的这种错误方法,来看看效果。原因可以用如下一个小例子来模拟。在于 a+b+c=1如果 你把a,b,c 同时扩大n倍,那么虽然a+b+c不再等于1,但是a,b,c之间的大小关系没有和原来是一样的。原来大的,扩大n倍依然大。
做自然语言处理的可以分为两大阵营,统计学派和规则学派。规则学派攻击统计学派是“碰运气”,理论基础不够严密,估计从上面的小例子可见端倪。
查阅过一些资料,几乎所有资料上有关概率建模都是(四)中的建模.我一直在想为啥一定要那么建模,别的建模方法能不能说得通?所以才有了(五)中的建模,从目前试验结果来看,(五)中的概率假设也是没有什么不可以的。



