数据结构（C#）：图的最短路径问题、（Dijkstra算法）
今天曾洋老师教了有关于图的最短路径问题，现在对例子进行一个自己的理解和整理：
题目：
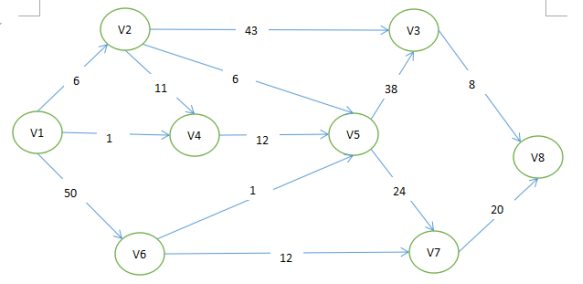
要求：变成计算出给出结点V1到结点V8的最短路径
答：
首先呢，我会先通过图先把从V1到V8的各种路径全部计算下来，如下：
（1）v1 -> v4 -> v5 -> v3 -> v8 => 1+12+38+8=59
（2）v1 -> v4 -> v5 -> v7 -> v8 => 1+12+24+20=57
（3）v1 -> v6 -> v5 -> v7 -> v8 => 50+1+24+20=95
（4）v1 -> v6 -> v7 -> v8 => 50+12+20=82
（5）v1 -> v2 -> v3 -> v8 => 6+43+8=57
（6）v1 -> v2 -> v5 -> v3 -> v8 => 6+6+38+8=58
（7）v1 -> v2 -> v5 -> v7 -> v8 => 6+6+24+20=56（最短路径）
（8）v1 -> v2 -> v4 -> v5 -> v3 -> v8 => 6+11+12+24+20=75
（9）v1 -> v2 -> v4 -> v5 -> v7 -> v8 => 6+11+12+24+20=73
从上面列出来的路径中，很清楚的看到（7）的路径数是最短的，那么，下面我们通过Dijkstra算法来确定从V1到其他数之间的最小距离分别是多少
步骤一：
先定义两个数组：
f：表示判断是否已经找到最短路径，1表示找到，0表示暂且没找到
d：表示当前最短路径
首先，从V1开始，f的第一个一定是1，因为它与它本身的距离一定是最短的（无距离）
d的第一个一定是0，因为V1和V1无算数概念可言，
接着V1分别与其他路径进行计算，必须是直接路径才算，不是直接路径的只能算是无穷大
（例如题中，V1到V2的距离为6，那么在d的数组中的距离就放入6，而V1到V3没有直接到达，需要经过V2，所以只能是无穷大）
如图所示：
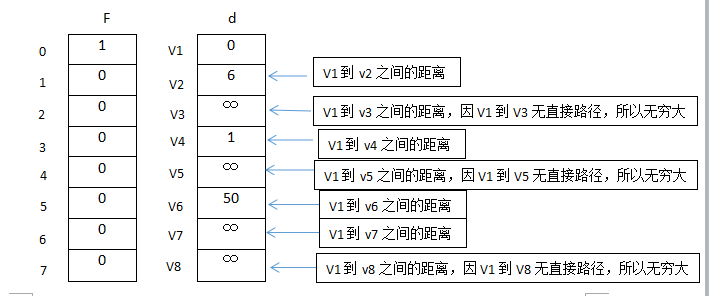
步骤二：
在输入完V1到其他数字的距离后，我们开始看d中的数字，在d的数组中，最小的数字为V4对应的1
那么，我们就把d中的V4为结点，把它相对应在f的位置从0改成1,（在f中，只要为1的，在d中相对应的数字在之后运算中都无需再改，因为它就是最短路径了）
接着，我们就可以从V1经过V4之后的所有路径进行计算了（在计算过程中，若数据比原数据大，就保留原数据，否则替换原数据）
如图所示：
步骤三：
在输入V4的所有数据后，我们再次看d中的数字，在d的数组中，最小的数字为V2对应的6
那么，这次我们把V6对应的数字为结点，在f中对应的0改成1
再通过V6与其他在f中为0，d中相对应的数据进行路径长短计算（在计算过程中，若数据比原数据大，就保留原数据，否则替换原数据）
如图所示：
步骤四：
在输入V4的所有数据后，我们再次看d中的数字，在d的数组中，最小的数字为V5对应的12
那么，这次我们把V5对应的数字为结点，在f中对应的0改成1
再通过V5与其他在f中为0，d中相对应的数据进行路径长短计算（在计算过程中，若数据比原数据大，就保留原数据，否则替换原数据）
如图所示：
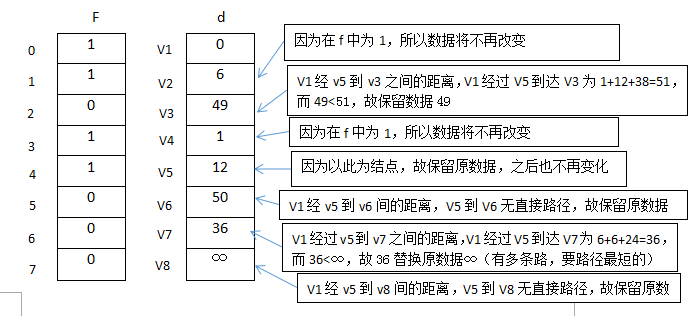
步骤五：
在输入V5的所有数据后，我们再次看d中的数字，在d的数组中，最小的数字为V7对应的36
那么，这次我们把V7对应的数字为结点，在f中对应的0改成1
再通过V7与其他在f中为0，d中相对应的数据进行路径长短计算（在计算过程中，若数据比原数据大，就保留原数据，否则替换原数据）
如图所示：
步骤六：
在输入V7的所有数据后，我们再次看d中的数字，在d的数组中，最小的数字为V3对应的49
那么，这次我们把V3对应的数字为结点，在f中对应的0改成1
再通过V3与其他在f中为0，d中相对应的数据进行路径长短计算（在计算过程中，若数据比原数据大，就保留原数据，否则替换原数据）
如图所示：
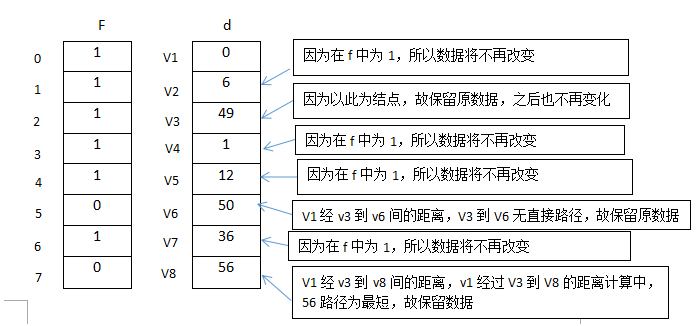
步骤七：
在输入V3的所有数据后，我们再次看d中的数字，在d的数组中，最小的数字为V6对应的50
那么，这次我们把V6对应的数字为结点，在f中对应的0改成1
再通过V6与其他在f中为0，d中相对应的数据进行路径长短计算（在计算过程中，若数据比原数据大，就保留原数据，否则替换原数据）
如图所示：
步骤八：
在输入V6的所有数据后，我们看到f数组中，只剩下了V8的数据为0，
那么，这次我们只要把V8在f中对应的0改成1，那么这次试题就结束了
如图所示：
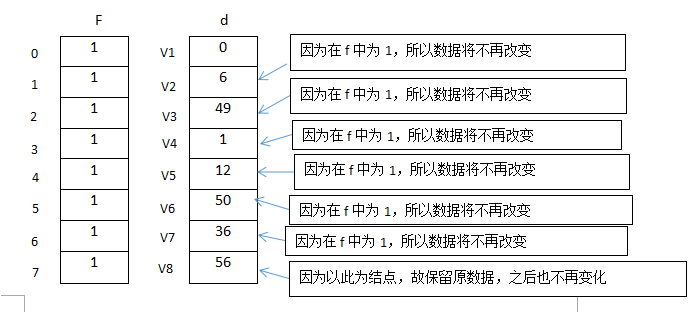
结果：
以V1为开始结点到其他的结点的最短距离分别是：
V1 -> V2 = 6
V1 -> V3 = 49
V1 -> V4 = 1
V1 -> V5 =12
V1 -> V6 = 50
V1 -> V7 = 36
V1 -> V8 = 56
END
