提高组算法-树状数组
树状数组是当序列动态变化时,依然可以高效率的查询和维护前缀和(或区间和)的数据结构。
实现思路
现在有 \(16\) 个数字:\(a[]={1,8,5,9,6,3,9,8,7,2,3,9,6,4,1,7}\)。
我们要实现 \(2\) 个函数:
-
修改其中某个元素的数值。
-
求出前 \(n\) 个数字的和。
但是,这 \(2\) 个函数要在极短的时间限制内解决数百万个以上操作。那该如何编写呢?
我们先从最原始的方法开始想:用 \(a\) 数组把数字存储,每次查询就遍历一遍。但是这样查询会非常的慢,可能运行到明年都运行不完。
那我们可以这样想:
把 \(a\) 数组的元素两两求和放入第 \(2\) 层,这样我们查询速度会快很多,每次也只需要多修改一个数字。照此方法:我们再把 第 \(2\) 层的元素两两求和,放入第 \(3\) 层。把 第 \(3\) 层的元素两两求和,放入第 \(4\) 层。以此类推。直到只剩 \(1\) 个元素为止。
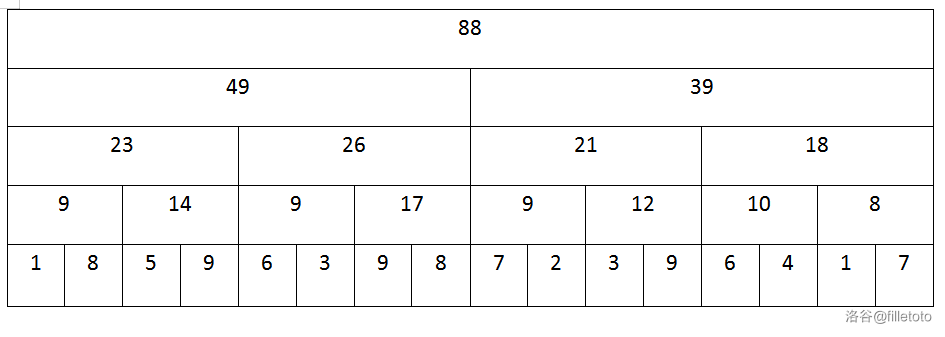
如果要计算前 \(7\) 个数字的和,也只需要计算成 \(23+9+9\) 就可以了,大大的加快了计算的速度。
但我们观察这个表,会发现许多数字根本不会用到!
例如:数字 \(14\),在计算前 \(3\) 个数字和直接 \(9+5\);在计算前 \(4\) 个数字的和直接用 \(23\);在计算前 \(5\) 个数字的和直接用 \(23+6\)。所以数字 \(14\) 根本就不需要使用,但想这样没用的数字还有很多。
所有层的第偶数个数字都是无用的,去掉了也不影响计算。即变成这个样子:
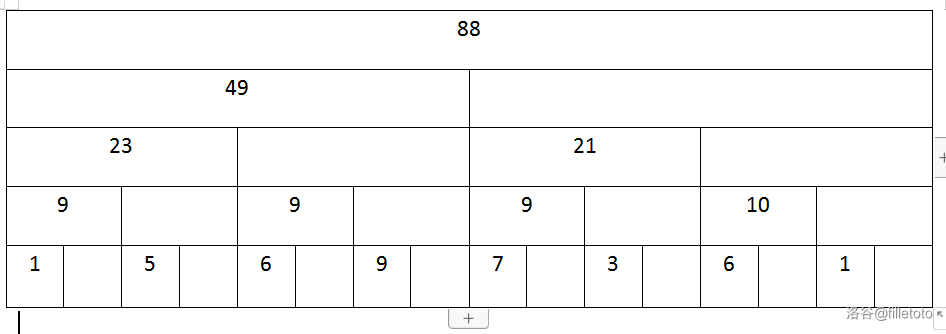
我们数一下数量,会发现,在这个表中剩下的数据刚好是 \(16\) 个。我们可以把这些数字都存储在数组 \(b\) 中,这个数组就是树状数组。
如上图,\(b[]={1,9,5,23,6,9,9,49,7,9,3,21,6,10,1,88}\)(按照后序遍历存储)
求和时,我们只要找到对应的区间并相加就可得出结果。
修改时,我们只需要向上找到包含他的区间进行修改即可。
听着很复杂,但他们的实现其实只要 \(10\) 行不到,那要具体实现他们,我们先来了解一下 lowbit 函数。
lowbit 函数
inline int lowbit(int x)
{
return x&(-x);
}
会求出数字 \(x\) 的二进制中最低位代表哪一个数字。
例如:\(x=70\),将 \(x\) 转换为二进制是 \(1000110\),他的最后一个 \(1\) 代表 \(2\),所以 \(70\) 的 lowbit 就是 \(2\)。
第一层的区间长度为 \(1\),而他们的 lowbit 也为 \(1\)。第二层的区间长度为 \(2\),而他们的 lowbit 也为 \(2\)。其他也是这样以此类推。序号为 \(i\) 的序列正好就是长度为 \(lowbit(i)\) 且以 \(i\) 结尾的序列。
还有一个性质,就是序列 \(b[i]\) 正上方的序列,正好就是 \(b[i+lowbit(i)]\)。
inline void add(int p,int x)
{
while(p<=n)
{
b[p]+=x;
p+=lowbit(p);
}
}
inline int sum(int x)
{
int ans=0;
while(x>0)
{
ans+=b[x];
x-=lowbit(x);
}
return ans;
}
单点修改+区间查询
#include <bits/stdc++.h>
using namespace std;
int n,b[500005],m;
inline int lowbit(int x)
{
return x&(-x);
}
inline void add(int p,int x)
{
while(p<=n)
{
b[p]+=x;
p+=lowbit(p);
}
}
inline int sum(int x)
{
int ans=0;
while(x>0)
{
ans+=b[x];
x-=lowbit(x);
}
return ans;
}
int main()
{
ios::sync_with_stdio(false);
cin>>n>>m;
for(int i=1;i<=n;i++)
{
int x;
cin>>x;
add(i,x);
}
while(m--)
{
int op,x,y;
cin>>op>>x>>y;
if(op==1)
{
add(x,y);
}
else if(op==2)
{
cout << sum(y)-sum(x-1) << endl;
}
}
return 0;
}


