二叉树
一.二叉树的概念
1.二叉树的性质
二叉树的每个节点最多有两个子节点,分别称为左孩子和右孩子,以他们为根的子树称为左子树和右子树。
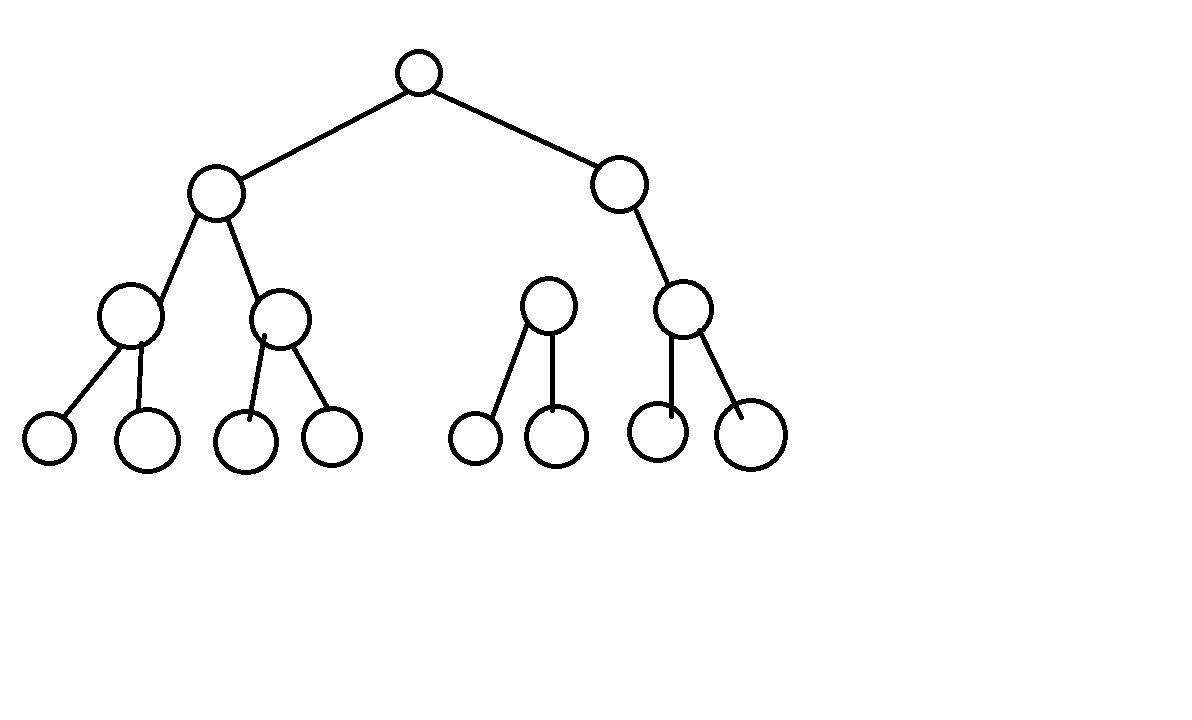
二叉树的第 i 层最多有 2^(i-1) 个节点。如果每层的节点数都是满的,称他为满二叉树。图例:
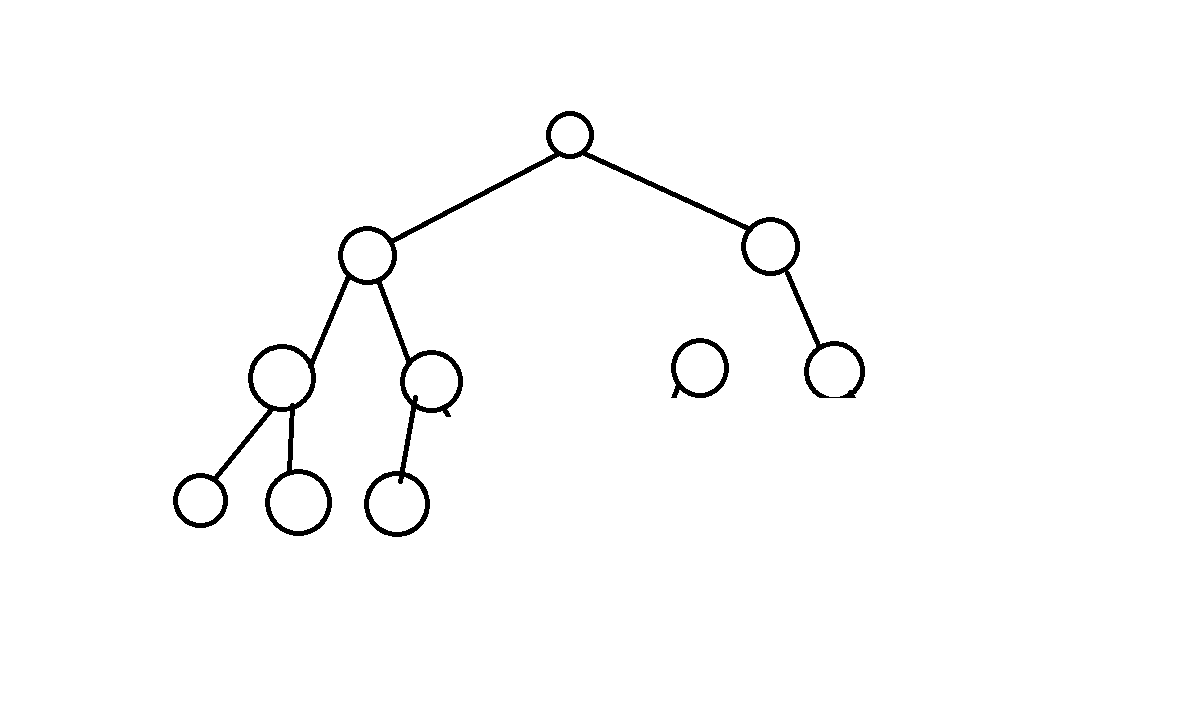
如果这个二叉树只是在最后一层有缺失,且缺失的编号都在最后,则成为完全二叉树。图例:
最上面的节点是二叉树的根,他是唯一没有父节点的节点。从根到节点 u 的路径长度定义为 u 的深度,节点 u 到它的叶子节点的最大路径长度定义为节点 u 的高度。根的高度最大,称为树的高。
二.二叉树的存储结构
二叉树一个节点的存储,包括节点的值,左右子节点,有静态和动态两种存储方法。
1.动态二叉树
struct Node { int value;//节点的值 node *lson,*rson;//指向左右节点 };
注意:需要管理,小心出错。
2.静态二叉树
struct Node { int value; int lson,rson;//左右孩子 }tree[N];
3.访问
一颗节点总数量为 k 的完全二叉树,设 1 号节点为根节点,有以下性质:
(1). 编号 i>1 的节点,其父节点编号为 i/2
(2). 如果 2i>k,那么节点 i 没有孩子;如果 2i+1>k,那么节点 i 没有右孩子
(3). 如果节点 i 有孩子,那么他的左孩子是节点 2i,右孩子是节点 2i+1
4.实战演练
洛谷p4913 代码:(根据上方访问的3个性质进行爆搜)
#include <iostream> using namespace std; int n; struct node { int l,r; }t[1000005]; int ans; inline void dg(int dep,int step) { if(dep==0) return ; ans=max(ans,step); dg(t[dep].l,step+1); dg(t[dep].r,step+1); } int main() { ios::sync_with_stdio(false); cin>>n; for(int i=1;i<=n;i++) { int x,y; cin>>x>>y; t[i].l=x; t[i].r=y; } dg(1,1); cout << ans << endl; return 0; }
洛谷p4715 代码:(根据上方访问的3个性质加上一些将数据转化为二叉树形式的思维)
#include <iostream> using namespace std; int n,a[(1<<7)+5],t[3505]; inline void dg(int x) { if(x>=(1<<n)) return ; dg(x*2); dg(x*2+1); int va=a[2*x],vb=a[2*x+1]; if(va>vb) { a[x]=va; t[x]=t[2*x]; } else { a[x]=vb; t[x]=t[2*x+1]; } } int main() { ios::sync_with_stdio(false); cin>>n; for(int i=0;i<(1<<n);i++) { cin>>a[i+(1<<n)]; t[i+(1<<n)]=i+1; } dg(1); cout << (a[2]>a[3]?t[3]:t[2]) << endl; return 0; }
二.二叉树的遍历
上图:

1.先序遍历
- 先访问根节点;
- 然后访问左子树;
- 最后访问右子树。
上图的先序遍历是 EBADCGFIH,伪代码如下:
void preorder(node *root) { cout << root->value; preorder(root->lson); preorder(root->rson); }
2.中序遍历
- 首先遍历左子树;
- 然后输出根结点;
- 最后遍历右子树;
void inorder(node *root) { inorder(root->lson); cout << root->value; inorder(root->rson); }
3.后序遍历
- 首先遍历左子树;
- 然后遍历右子树;
- 最后输出根结点;
void postorder(node *root) { postorder(root->lson); postorder(root->rson); cout << root->value; }
4.实战演练
代码:
#include <iostream> using namespace std; struct node { int val; int l,r; }t[1000005]; int n,l,r; inline void pre(int root) { cout << t[root].val << " "; if(t[root].l!=0) { pre(t[root].l); } if(t[root].r!=0) { pre(t[root].r); } } inline void in(int root) { if(t[root].l!=0) { in(t[root].l); } cout << t[root].val << " "; if(t[root].r!=0) { in(t[root].r); } } inline void post(int root) { if(t[root].l!=0) { post(t[root].l); } if(t[root].r!=0) { post(t[root].r); } cout << t[root].val << " "; } int main() { ios::sync_with_stdio(false); cin>>n; for(int i=1;i<=n;i++) { cin>>l>>r; t[i].l=l; t[i].r=r; t[i].val=i; } pre(1); cout << endl; in(1); cout << endl; post(1); return 0; }
三.二叉树的前中后序遍历提高
1.通过前序中序遍历来求后序遍历
四.二叉堆
一.堆的性质
-
堆是一颗完全二叉树
-
堆的顶端一定是“最大”,最小”的,但是要注意一个点,这里的大和小并不是传统意义下的大和小,它是相对于优先级而言的,当然你也可以把优先级定为传统意义下的大小,但一定要牢记这一点,初学者容易把堆的“大小”直接定义为传统意义下的大小,某些题就不是按数字的大小为优先级来进行堆的操作的
-
堆一般有两种样子,小根堆和大根堆,分别对应第二个性质中的“堆顶最大”“堆顶最小”,对于大根堆而言,任何一个非根节点,它的优先级都小于堆顶,对于小根堆而言,任何一个非根节点,它的优先级都大于堆顶(这里的根就是堆顶啦qwq)
二.堆的插入
事实上堆的插入就是把新的元素放到堆底,然后检查它是否符合堆的性质,如果符合就丢在那里了,如果不符合,那就和它的父亲交换一下,一直交换交换交换,直到符合堆的性质,那么就插入完成了
上图:

代码:
inline void puts(int x) { a[++tot]=x; for(int y=tot;y>1;) { if(a[y]<a[y>>1]) { swap(a[y],a[y>>1]); y=y>>1; } else return ; } }
三.堆的删除
代码中是直接把堆顶和堆底交换一下,然后把交换后的堆顶不断与它的子节点交换,直到这个堆重新符合堆性质~~(但是上面的方式好理解啊)~~
手写堆的删除支持任意一个节点的删除,不过STL只支持堆顶删除,STL的我们后面再讲
上图:

代码:
inline int gets() { int x=a[1]; a[1]=a[tot--]; for(int y=1;(y<<1)<=tot;) { int k=y; if(a[y<<1]<a[k]) k=y<<1; if(((y<<1)+1<=tot)&&(a[(y<<1)+1]<a[k])) { k=(y<<1)+1; } if(k==y) return x; swap(a[k],a[y]); y=k; } return x; }
四.堆查询
因为我们一直维护着这个堆使它满足堆性质,而堆最简单的查询就是查询优先级最低/最高的元素,对于我们维护的这个堆heap,它的优先级最低/最高的元素就是堆顶,所以查询之后输出heap[1]就好了
一般的题目里面查询操作是和删除操作捆绑的,查询完后顺便就删掉了,这个主要因题而异。
完结撒花!!!


