CG: 投影几何与齐次坐标 Projective Geometry / Homogeneous Coordinates
Abstract
我在入门计算机图形学过程中,许多文献书籍在解释成像原理时总是单刀直入地将齐次坐标捆绑在透视投影的推导中,令我一时难以接受如此“新鲜”的概念;在很长一段时间里,齐次坐标对我来说是一种很神秘的符号,它的 \(w\) 分量是如此抽象而晦涩。
于是在查阅大量内外网资料后,我对齐次坐标所构建的系统有了认知。我相信这篇小文能对理解计算机世界中的投影几何的本质有一定的帮助。本文我会循序渐进构建一些知识体系,并用一丝丝拙略的数学口吻来描述;若有任何不恰当的错误,还请劳烦您向我指正!
投影几何 Projection Geometry
欧几里得几何学很好地描述了我们的三维世界,然而当考虑到相机的成像过程时,很明显欧几里得几何不够用:长度和角度不再可靠,平行线可能会相交。所以有了投影几何,它是对欧几里得几何的扩展。
笔者寄语:当你理解这篇文章的每个部分后,我相信你至少能在面对与投影几何相关的工作(图形、游戏编程)时有足够的底气。文中只有一点点数学计算,相信难不倒聪慧的你 😃
投影平面 Projection Plane
当你端着画板对风景进行写生、用相机记录美好瞬间时,你无不正与投影几何所打交道。
写生时,投影平面便是你的画板;假设你是一个神人,你握着铅笔的那只手上长了一只眼睛,这只眼睛甚至能透视 --- 穿过画板看到目标景观,并精确捕捉颜色,指挥手来绘画。

此时我们便说,“眼睛” 透视 画板,将看到的风景颜色投影到了 投影 平面上。
我们将这种十分直白的现象抽象一下:
存在一个视点(相机),一个投影平面,和需要被投影至面上的点;另外,我们习惯于将视点置于经典笛卡尔坐标系的原点 \(O\) 。
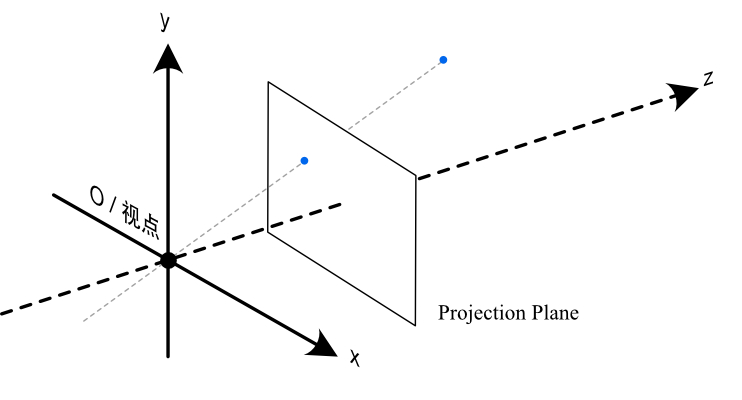
投影几何点 Points in Projective Geometry 与齐次坐标 Homogeneous Coordinates
齐次坐标
三维空间中点的坐标通常用 \((x, y, z)\) 表示;而齐次坐标便是在当前维度的坐标表示下,为其扩展一个分量 \(w\) ,使其变为 \((x, y, z, w)\) 。
我们做本文第一个重要的约定:
齐次坐标只有在应用于 投影几何系统中的点 时,才具有实际意义,并且这种点称为 “投影几何点” ;
而当应用于普通坐标系统中的点时,齐次坐标便不具有实际意义,并且这种点称为 “普通点” 。
旁注:本文的“齐次坐标”与线性变换中的“齐次坐标”体现的功能性不同,请不要迷失
区分投影几何点与普通点
为了方便计算机处理,我们将齐次坐标表示均应用于 “普通点” 与 “投影几何点”,并用一种方法对它们进行区分。
现在,我们做本文第二个重要的约定:(在阅读本文时,请一定谨记这个约定,它将成为你区分投影几何点 / 普通点的功臣)
有一个齐次坐标表示的点 \(P(x, y, z, w)\) ,当且仅当 \(P\) 满足以下条件:
- 当 \(w = 1\) 时 ,\(P\) 正好位于投影平面 \(z = n\) 上
此时将 \(P\) 称为 投影几何点 ;任何不满足此条件的点,一律称为 普通点 。以下是一个直观例子:
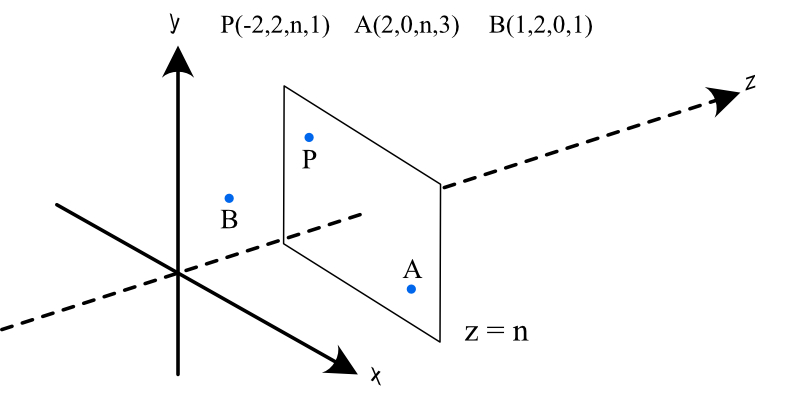
显然,只有点 \(P\) 满足条件,所以它是一个 投影几何点 ,而 \(A\) 、\(B\) 为 普通点。
此时你一定会发问:“什么叫 '当 \(w = 1\) 时' ?\(w\) 依据什么而改变?” 那么,我将为你解开疑惑。
\(w\) 的功能
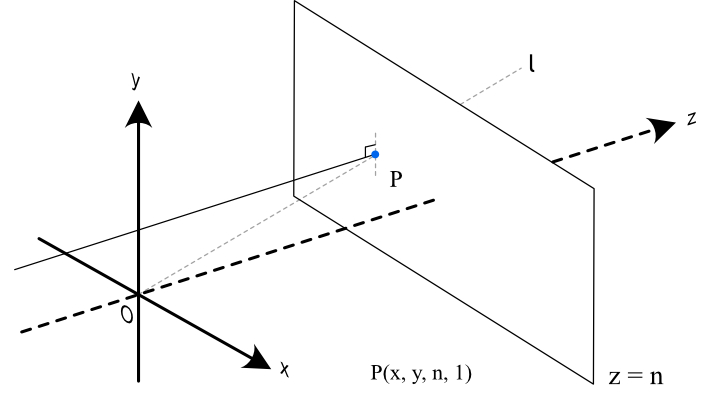
有一 投影几何点 \(P(x, y, n, 1)\) 位于投影平面 \(z = n\) 上。一条视线从视点 \(O\) 出发,穿过 \(P\) 并直入深邃的空间中;
我们将 \(P\) 沿着 \(l\) 往上走一段距离,变成 \(P^{'}(x^{'}, y^{'}, m, w^{'})\)

我们离近点看,争取将 \(P^{'}\) 算出来:(推导稍许冗长,你可以选择直接看结论,但我建议你了解其中的细节 😃 )
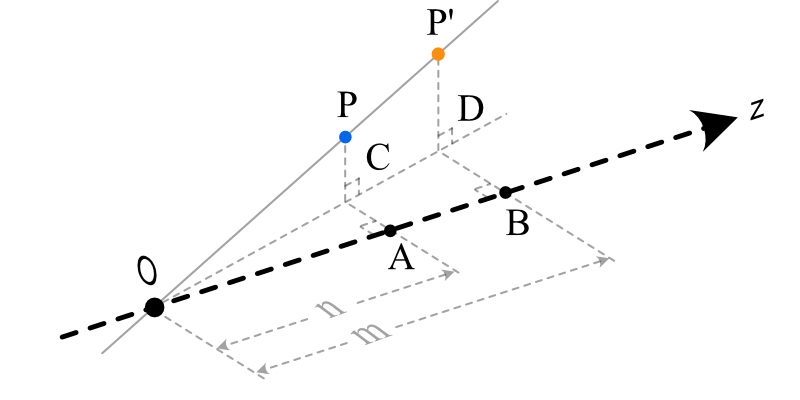
分别做点 \(P\) 、\(P^{'}\) 的垂线 \(PC\) 、\(P^{'}D\) ,并分别与平面 \(y = 0\) 交于点 \(C\) 、\(D\) ;再于 \(z\) 轴上找到 \(A\) 、\(B\) ,分别做它们的垂线,与点 \(C\) 、\(D\) 相交,则 \(OA = n\) ,\(OB = m\)。
由相似三角形关系:
\( \triangle OAC \sim \triangle OBD\\ \Rightarrow \frac{AC}{BD} = \frac{OA}{OB}\\ \Rightarrow BD = P^{'}_{x} = \frac{AC \cdot OB}{OA} = P_{x} \cdot \frac{m}{n}\ \ \ (1) \)
由平行关系:
\( AC\ \verb|//|\ BD\\ \Rightarrow \frac{OC}{OD} = \frac{OA}{OB}\ \ \ (2) \)
由相似三角形关系:
\( \triangle OCP \sim \triangle ODP^{'}\\ \Rightarrow \frac{PC}{P^{'}D} = \frac{OC}{OD}\\ \Rightarrow P^{'}D = P^{'}_{y} = \frac{PC \cdot OD}{OC} = P_{y} \cdot \frac{OD}{OC}\ \ \ (3) \)
联立 \((2)(3) \Rightarrow P^{'}_{y} = P_{y} \cdot \frac{OB}{OA} = P_{y} \cdot \frac{m}{n}\ \ \ (4)\)
有了结论 \((1)(4)\) ,我们便能写出点 \(P^{'}\) 的坐标:\(P^{'} = (x \cdot \frac{m}{n},\ y \cdot \frac{m}{n},\ m,\ w^{'})\) 。呼,推导真费头发,我保证这是最后一次了。
对比一下 \(P\) 与 \(P^{'}\) 的坐标,我们能得出什么结论:
\(P^{'} = \frac{m}{n} \cdot P\) ,也即是,点 \(P^{'}\) 与点 \(P\) 关于 \(\frac{m}{n}\) 线性相关。现在你要问我 \(w^{'}\) 该变成什么,我会毫不犹豫地回答:\(\frac{m}{n}\) :
\(P^{'} = (x \cdot \frac{m}{n},\ y \cdot \frac{m}{n},\ m,\ \frac{m}{n})\)
现在你应该对分量 \(w\) 有某种微妙的认知,它并不是一个空间上的维度,而是一个线性缩放的因子,不是吗?
当点 \(P\) 离开平面 \(z = n\) 在视线 \(l\) 上移动时,\(w\) 将成为一个缩放因子,线性地改变 \(P\) 各分量的值。你或许会嘲笑我说:"点P离开了平面,w又变成了一个不是1的值,那它岂不变成了一个普通点?"
现在,就是展示投影几何威力的时刻。 想象点 \(P^{'}\) 就是我们想写生的景物,此时你的神奇的手使出绝技:“吸星大法!” --- 你对 \(P^{'}\) 的所有分量同时除以它的 \(w\) ,\(P^{'}\) 瞬间变成了 \(P\) ,并被“吸”回投影平面 \(z = n\) ------- 这便是大名鼎鼎的 透视除法 !透视除法的目标便是将 投影几何点 的 \(w\) 分量变为 \(1\) ,这样点就能回到投影平面上。
而从另一个角度看,\(P \rightarrow P^{'}\) 之间可通过除法相互转换,推广到视线 \(l\) 上的所有点,它们都能通过 \(P\) 乘一个缩放因子来相互转化。因此我们进行第三次约定:
-
我们说 投影几何系统中的直线 指的是视线(穿过原点的任意直线)
-
在投影几何中,每一条直线(视线)都可当作一个点( 投影几何点 )
-
在同一条视线上,所有点其实都是同一个点
因为只有视线符合“投影”的语境:视线要么与投影平面有一个交点,要么平行于投影平面,无任何交点,不是吗?
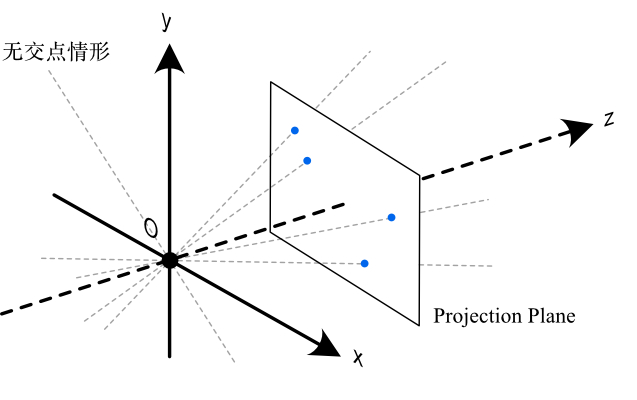
普通点
只有在规定好了一个投影平面 \(z = n\) 时,才能构建与它配套存在的 投影几何点(视线):
\(P = (x, y, n, 1)\) 或 \(P = (\frac{m}{n}x, \frac{m}{n}y, m, \frac{m}{n})\)
面对点 \(A = (2, 0, n, 3)\) 时,你或许会说“ \(A\) 正好在 \(z = n\) 上,它看起来也是一个 投影几何点 呀”。
但你若换个角度,将 \(A\) 除以它的 \(w\) 分量变为
\(A^{'} = (\frac{2}{3}, 0, \frac{n}{3}, 1)\)
呃, \(w = 1\) ,你想到了什么?

没错,在由围绕投影平面 \(z = n\) 架构的投影几何系统中, \(A\) 是一个 普通点 ;而在由围绕 \(z = \frac{n}{3}\) 构建的投影几何系统中, \(A\) 却是一个关于 \(z = \frac{n}{3}\) 的 投影几何点 。
于是我们便可以得出结论, \(A\) 之所以为一个 普通点,是因为它在我们规定的与 \(z = n\) 相关的投影几何系统中不适用 ------ 为它执行透视除法后,它不能回到 \(z = n\) 上。所谓 普通点 与 投影几何点 ,均是由人为规定,存在于一定的参照条件下(投影平面)而自洽的;
但若离开 “我欲'透视'并将某物'投影'到我的画板上” 这样的语境时,将不会存在投影平面,也不用区分 普通点 与 投影几何点。 投影几何系统也瞬间崩塌,所有处于三维笛卡尔空间中的点均恢复为最为普通的,也是我们最为熟知的经典笛卡尔坐标点。
透视除法矩阵 Perspective Division Matrix
很好,我们现在能区分 普通点 与 投影几何点。我们在之前还说
透视除法的目标便是将 投影几何点 的 \(w\) 分量变为 \(1\),这样点就能回到投影平面上。
之前的讨论中,我们为透视除法赋予了一种操纵几何变换关系的能力,它只能应用于 投影几何点 。
但回到我们工作 / 学习的环境,计算机在对齐次坐标进行线性变换计算时不可能完美地将所有顶点处理成 投影几何点 ;事实上,顶点在一开始或被计算的过程中,大部分都是 普通点 ,它们没办法通过除以 \(w\) 来投影到我们规定好的平面上。
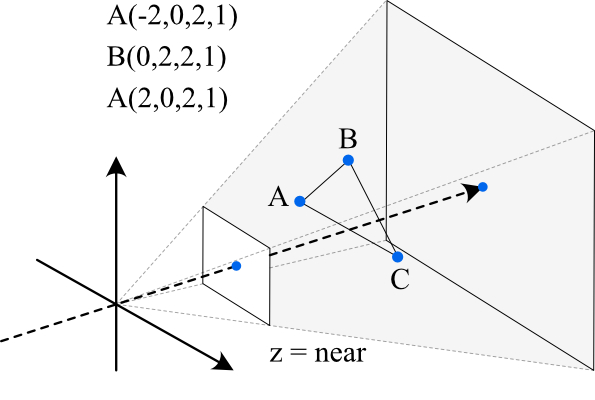
觉得熟悉吗?在工作 / 学习环境中,投影平面是 \(z = near\) ,我们输入的三角面片的世界坐标一般都如图中 \(ABC\) 这样。显而易见,它们均是 普通点;但我们又想将它们投射到 \(z = near\) 上,然而透视除法无法应用于这样的点。
所以人们想到一种办法,来将一个 普通点 变换到已构建好的投影几何系统中,并让它变为一个 投影几何点 , 这样一来,便可以顺理成章地将它“吸”回投影平面。这便是 透视除法矩阵 的工作:
设已存在投影平面 \(z = n\) ,一 普通点 \(P(x, y, m, w)\) 。现在构建 透视除法矩阵:
\(\left[\begin{array}{cccc}1 & 0 & 0 & 0\\ 0 & 1 & 0 & 0\\0 & 0 & 1 & 0\\0 & 0 & \frac{1}{n} & 0\end{array}\right]\left[\begin{array}{c}x\\y\\m\\w\end{array}\right] = \left[\begin{array}{c}x\\y\\m\\\frac{m}{n}\end{array}\right]\)
你会发现,该矩阵的效果仅为将比例 \(\frac{m}{n}\) 赋予 \(P\) 的 \(w\) 分量。要我来说,这个矩阵应该叫做 将普通点转换为投影几何点矩阵 (意思一下,不要当真)。
\(P\) 此时真的成为了 投影几何点 --- 不信将它除以 \(w\) ,变为:
\(P = (\frac{n}{m}x,\ \frac{n}{m}y,\ n,\ 1)\)
很神奇,不是吗?变换后的 \(P\) 能名正言顺地应用透视除法并回到 \(z = n\) , \(w\) 还等于 \(1\) !
尾声:无穷远点 Points at Infinity / 齐次坐标的 \(z\rightarrow0\) 会怎样
我们将投影平面画得不那么秀气一点。做一条垂直于 \(z = n\) 且穿过 \(P\) 的直线,以观察当 \(P\) 朝着 \(P_{z} \rightarrow 0\) 的方向上移动时,会发生什么。
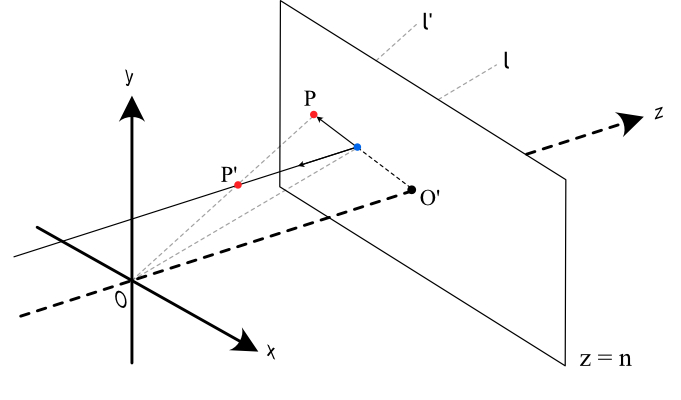
将 \(P\) 沿垂线后退一些,变为 \(P^{'}(x^{'}, y^{'}, m, w^{'})\) 。为了再次将 \(P^{'}\) 投影回去,对其应用透视除法矩阵,并执行透视除法,则 \(P^{'}\) 重新成为新投影点 \(P(\frac{n}{m}x,\frac{n}{m}y,n,1)\) ,同时视线 \(l\) 变为 \(l^{'}\) 。
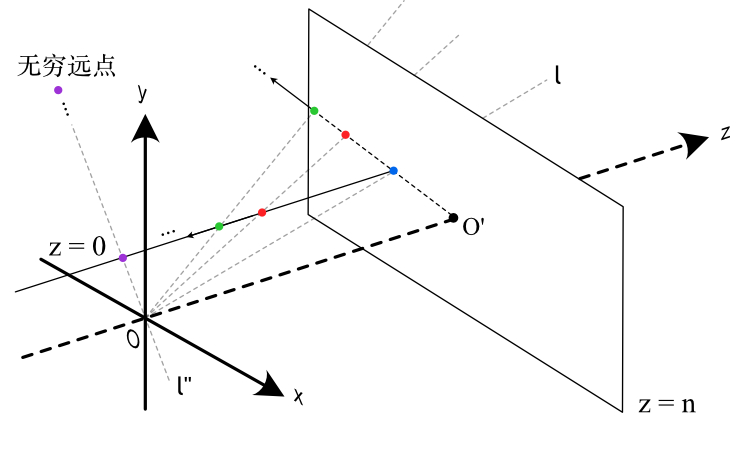
当 \(P^{'}\) 越往里移动,投影点离投影屏幕中心 \(O^{'}\) 越来越远;当 \(P^{'}_{z} \rightarrow 0\) 时,投影点与 \(O^{'}\) 的距离近乎无限大,且会收敛为视线 \(l^{''}\) 平行于投影屏幕的情形。此时我们说此投影点或者视线 \(l^{''}\) 是一个无穷远点。
至此关于投影几何的介绍基本完结。如果你觉得有什么遗漏或者错误,欢迎用博客园的评论或私信系统告诉我。
创作不易,转载请注明出处 😃





