杂谈: 仿射变换 Affine Transformation
Abstract
在网络上多方查证后,发现仿射变换并不如它的命名那样高深莫测。但秉承着对Computer Graphics这门科学的敬畏,还是决定对其深入研究一番。
释义
“仿射”一词真是让人摸不着头脑,首先从它入手:
-
根据Wikipedia的解释,仿射变换,或者说Affinity(源于拉丁语affinis,"connected-with",与..相关联的)是一种能保持线与线之间的平行性的几何变换(不包括距离和角度)。
-
若X是仿射空间的一个点集,那么X上的所有仿射变换都可以表示为X上的线性变换和平移的组合。与纯线性变换不同,仿射变换不需要保持仿射空间的原点不变。因此,每个线性变换都是仿射变换,但不是每个仿射变换都是线性变换(线性变换是仿射变换的子集)。
-
对于一个向量空间,一个任意的仿射变换都能表示为乘以一个矩阵 (线性变换) 接着再加上一个向量 (平移)。
综上所述,仿射变换可表示:
- 旋转(线性变换)
- 缩放(线性变换)
- 平移(向量加)
事实上,仿射变换代表了对象变换前后的关系。
扩展
如上讨论,仿射变换是两种函数的组合:线性映射和平移映射。普通向量代数采用矩阵来表示线性映射,用矢量加法来表示平移。
- 从目前形式来看,在有限维的情形下,若线性映射由可逆矩阵\(A\)的乘法来表示,且平移由加上一个矢量 \(\bf{b}\) 表示,那么一个作用于矢量 \(\bf{x}\) 的仿射映射可被表示为:
\(\bf{y} = f(\bf{x}) = A\bf{x} + \bf{b}\)
用高一维度的线性变换来表示低维度的仿射变换
考虑增广矩阵augmented matix以及增广矢量技术,通过它们,可用一个单独的线性矩阵变换来表示仿射变换。
现在,对于原平移矢量 \(\bf{b}\),在其末尾增广一个维度“1”;对于原线性变换矩阵\(A\),在其底部增广一行“0”,并在其右边增广一个由 \(\bf{b}\) 表示的列:
\( \left [ \begin{array}{c} \begin{matrix} \bf{y} \\ 1 \end{matrix} \end{array} \right ] = \left [ \begin{array}{c:c} \begin{matrix} A\\ 0 ... 0 \end{matrix}& \begin{matrix} \bf{b}\\ 1 \end{matrix} \end{array} \right ] \left [ \begin{array}{c} \begin{matrix} \bf{x} \\ 1 \end{matrix} \end{array} \right ] \) ,这个式子等价于 \(\bf{y} = A\bf{x} + \bf{b}\),而这个增广矩阵即被称为仿射变换矩阵Affine Transformation Matrix。
实际例子
考虑一个二维向量空间中一个正方形点集被应用一个旋转加平移的仿射变换:
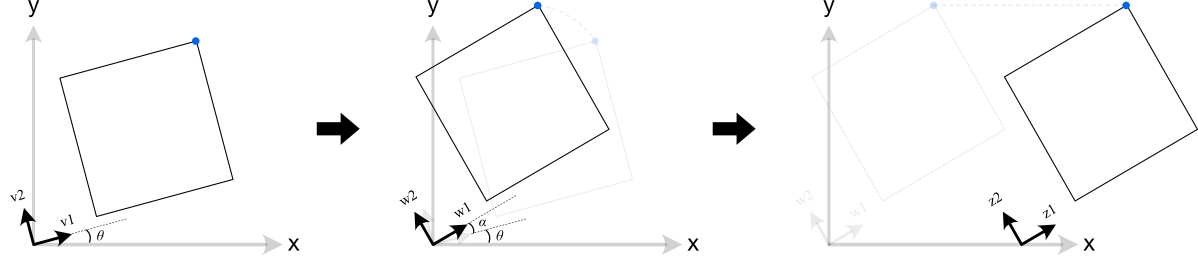
设正方形上任意点为\(\left[\begin{array}{cc}x & y\end{array}\right]^T\),对应变换后的点为\(\left[\begin{array}{cc}x^{'} & y^{'}\end{array}\right]^T\),平移矢量为 \(\bf{b} = \bf{(i, j)}\),则可列等式:
\(\left[\begin{array}{c}x^{'} \\ y^{'}\end{array}\right] = \left[\begin{array}{cc}cos\alpha & -sin\alpha\\ sin\alpha & cos\alpha\end{array}\right]\left[\begin{array}{c}x \\ y\end{array}\right] + \left[\begin{array}{c}i \\ j\end{array}\right]\)
我们将这个二维向量空间提升一个维度,并根据之前的讨论得到一个新变换矩阵:
\(\left[\begin{array}{c}x^{'} \\ y^{'} \\ 1\end{array}\right] = \left[\begin{array}{ccc}cos\alpha & -sin\alpha & i\\ sin\alpha & cos\alpha & j \\ 0 & 0 & 1\end{array}\right]\left[\begin{array}{c}x \\ y \\ 1\end{array}\right]\)
可以看到,通过增广矩阵这种技术,我们成功将“向量加”这种基于仿射变换的步骤成功并入一个线性变换中,也即相比于之前的等式,新等式是一个线性映射。
-
对于非几何意义,增广矩阵技术有利于计算机仅专注于处理矩阵乘法。
-
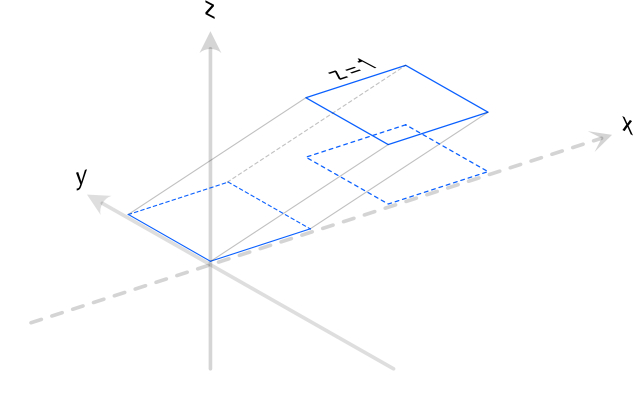
讨论几何意义,首先将最符合直觉的“升维”表现出来:增广的维度值为1,相当于将原待变换点集由二维向量空间升维至三维向量空间,且落在平面 \(z = 1\) 上。此时可想象升维前与升维后的点集之间连成一个立方体,升维前点集的平移仿射变换即可由这个立方体的线性变换完成,在这个图中,线性变换体现在将\(Z\)轴正方向的基进行了旋转。
如有不严谨的地方欢迎指出 😃





