Github TinyRenderer渲染器课程实践记录: Bresenham直线绘制算法
Abstract
Bresenham直线绘制算法。
Reference :
作为计算机图形学中最基础的画线段,我们从浅入深地进行探索。
版本1 --- 简单的线性插值
void line(int x0, int y0, int x1, int y1, TGAImage &image, TGAColor color) {
for (float t=0.; t<1.; t+=.01) {
int x = x0 + (x1-x0)*t;
int y = y0 + (y1-y0)*t;
image.set(x, y, color);
}
}
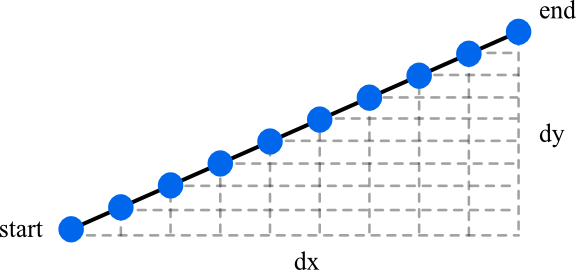
这种算法非常简单,分别在 \(xy\) 位移方向上进行平均采样并画点。采样率越高(t的步长)直线越精确。
版本2 --- 另一种线性插值
你会发现版本1使用了用户自定义的采样率( \(0\) 到 \(1\) ,步长为 \(0.1\) ),这样有点低效。 若直接选择 \(x\) 位移方向上的采样作为线性插值的自变量是否比较自然呢?
void line(int x0, int y0, int x1, int y1, TGAImage &image, TGAColor color) {
for (int x=x0; x<=x1; x++) {
float t = (x-x0)/(float)(x1-x0);
int y = y0 + (y1 - y0)*t;
image.set(x, y, color);
}
}

但这仍然存在大问题:当执行以下调用时,第二条线全是孔隙,而第三条根本没被绘制:
line(13, 20, 80, 40, image, white);
line(20, 13, 40, 80, image, red);
line(80, 40, 13, 20, image, red);
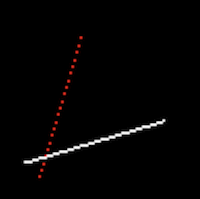
我们检查一下第二条直线有很多孔隙的原因。观察第二条 line 调用你会发现两点在 \(y\) 方向上的位移是大于 \(x\) 方向的,这导致的结果是,若执意在位移较小的 \(x\) 方向上进行采样,采样率(能取到点的个数)会比较小。
至于第三条线根本没绘制的原因,是因为第一个点的 \(x\) 值一开始就大于第二个点,所以导致根本不会进入绘制循环 :p
版本3 --- 加入边界判断
我们通过一些边界判断来修复可能会出现的错误。
void line(int x0, int y0, int x1, int y1, TGAImage &image, TGAColor color) {
bool steep = false;
if (std::abs(x0-x1)<std::abs(y0-y1)) {
std::swap(x0, y0);
std::swap(x1, y1);
steep = true;
}
if (x0>x1) {
std::swap(x0, x1);
std::swap(y0, y1);
}
for (int x=x0; x<=x1; x++) {
float t = (x-x0)/(float)(x1-x0);
int y = y0*(1.-t) + y1*t;
if (steep) {
image.set(y, x, color);
} else {
image.set(x, y, color);
}
}
}
-
第一个判断块修复采样率较低的问题。判断最大位移方向是否为y方向,若是则分别交换始终点 \(xy\) 顺序。假设出现了最大位移为y方向的情况,交换xy位置后,在之后的绘制循环中的采样方向一定是y方向。
-
第二个判断块修复了始终点顺序问题。
-
绘制循环中,steep为真代表直线较陡的情况,也即最大位移方向为 \(y\) 的情形。此时画点时需要再次调换一下采样点 \(xy\) 顺序。
中点Bresenam算法
首先我们有了直线两端点 \(A(x_{0}, y_{0})\) 和 \(B(x_{1}, y_{1})\),并设直线方程为
\(F(x, y) = y - kx - b\),由两端点容易得到斜率 \(k = \frac{y_{1} - y_{0}}{x_{1} - x_{0}}\)
先提前引入一个事实:将任意一个点带入\(F(x, y)\)后,若\(F(x, y) > 0\)说明此点在直线上方;若\(F(x, y) < 0\)说明在直线下方;若等于0则表示点刚好落在直线上。

Bresenham的思想就是,每次在最大位移方向上前进一个单位,而在另一个方向上是否前进取决于判别式。至于为什么要选择最大位移方向,会涉及到直线的反走样,详见我
对DDA算法解析的文章数值微分直线生成算法(DDA)。
\(0 \leq k \leq 1\)的情形
此时截距\(x_{1} - x_{0} > y_{1} - y_{0}\),也即最大位移方向为X轴正向。因此在计算下一个点\(x_{i+1}\)时,在\(X\)方向行进1,需确定下个点的\(y\)值是否加1:
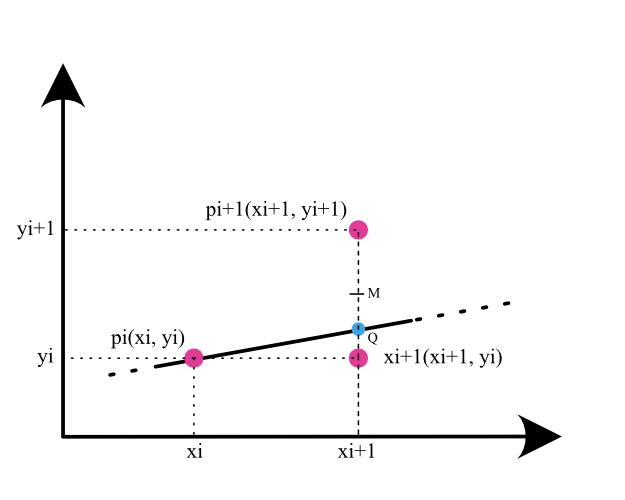
如图,我们的下一个理想绘制点其实应该是直线与\(x = x_{i} + 1\)的交点\(Q\),但是由于像素是离散的,仅有整数值,我们只能将这个交点近似地交由\(Q\)上面或下面的离散点来表
示。判断方法很简单,看交点\(Q\)在两个备选点的中点\(M\)的上面还是下面,反过来判断即为看中点\(M\)在\(Q\)的上面还是下面,若在\(Q\)的上面,则下一个点的\(y\)不变;若在\(Q\)下面,
则下一个点的\(y\)移动一个步长。
判别式:\(d_{i} = F(x_{M}, y_{M}) = F(x_{i} + 1, y_{i} + 0.5) = y_{i} + 0.5 - k(x_{i} + 1) - b\)
此时可将中点\(M(x_{i} + 1, y_{i} + 0.5)\)带入\(F(x, y)\),若结果\(d_{i} > 0\),表示点\(M\)在\(Q\)之上,此时下一个绘制点确定为\((x_{i} + 1, y_{i})\);反之确定为\((x_{i}+1, y_{i}+1)\);若\(d_{i} = 0\),表示
Q正好和M重合,那么我们默认下一个点取\(y\)不变的那个:
\(x_{i+1} = x_{i} + 1\)
\( \begin{equation}y_{i+1} = \begin{cases} y_{i} + 1 & (d_{i} < 0)\\ y_{i} & (d_{i} \geq 0) \end{cases} \end{equation} \)
判别式的推导
计算下一个绘制点时:
\(d_{i} < 0\)
取右上方点\(P_{u}(x_{i} + 1, y{i} + 1)\)。现在再判断下下一个点如何计算,即:
\( \begin{equation} \begin{aligned} d_{i+1} &= F(x_{i} + 2, y_{i} + 1.5) \\ &= y_{i} + 1.5 - k(x_{i} + 1) - b - k \\ &= di + 1 - k \end{aligned} \end{equation} \)
也即当\(d_{i} < 0\)时,\(d_{i+1}\)对于\({d_{i}}\)的增量为\(1-k\)
\(d_{i} \geq 0\)
取正右方点\(P_{d}(x_{i} + 1, y{i})\)。现在再判断下下一个点如何计算,即:
\( \begin{equation} \begin{aligned} d_{i+1} &= F(x_{i} + 2, y_{i} + 0.5) \\ &= y_{i} + 0.5 - k(x_{i} + 1) - b - k \\ &= di - k \end{aligned} \end{equation} \)
也即当\(d_{i} \geq 0\)时,\(d_{i+1}\)对于\({d_{i}}\)的增量为\(-k\)
代码中当然需要得到\(d_{i}\)的初值。显然直线的第一个像素\(p_{0}\)一定在直线上,因此可计算:
\( \begin{equation} \begin{aligned} d_{0} &= F(x_{0} + 1, y_{0} + 0.5) \\ &= y_{0} - kx_{0} - b - k + 0.5 \\ &= 0.5 - k \end{aligned} \end{equation} \)
注意这里的推导,由\(p_{0}\)在直线上的原因,\(y_{0} - kx_{0} - b = 0\)
看看我们推出了哪些需要的东西:
当\(d_{i} < 0\)时,\(d_{i+1}\)对于\(d_{i}\)的增量\((1)1-k\),进一步写作\(1-\frac{\Delta y}{\Delta x}\)
当\(d_{i} \geq 0\)时,\(d_{i+1}\)对于\(d_{i}\)的增量\((2)-k\),进一步写作\(-\frac{\Delta y}{\Delta x}\)
以及\(d_{0} = 0.5 - k\),进一步写作\(0.5 - \frac{\Delta y}{\Delta x}\)
我们只需判断判别式的正负,且希望尽量用整数来进行运算以加快速度,所以对这三个变量同时乘以\(2\)再乘以\(\Delta x\)来消除浮点运算:
(1) \(2\Delta x-2\Delta y\) (2) \(-2\Delta y\) (3) \(\Delta x - 2\Delta y\)
加入最大位移方向修正后,现在可以用代码来表示这个算法了(注意,若另一个方向上也即 \(dy\) 方向的起点坐标大于终点坐标,那么这个方向的步长改为-1即可):
void Bresenham(int x0, int y0, int x1, int y1, TGAImage &image, TGAColor color) {
// 确保x为最大位移方向
bool steep = false;
if (std::abs(x0-x1)<std::abs(y0-y1)) {
std::swap(x0, y0);
std::swap(x1, y1);
steep = true;
}
// 确保计算方向为正向
if(x0 > x1) {
std::swap(x0, x1);
std::swap(y0, y1);
}
int dX = std::round(fabs(x1 - x0));
int dY = std::round(fabs(y1 - y0));
int delta = dX - 2 * dY;
int dStepUp = 2 * (dX - dY);
int dStepDown = -2 * dY;
int x = x0, y = y0;
for(int i = x; i <= x1; i++) {
!steep ? image.set(i, y, color)
: image.set(y, i, color);
if(delta < 0) {
y += (y0<y1?1:-1);
delta += dStepUp;
} else {
delta += dStepDown;
}
}
}
此代码具有较好鲁棒性,无论端点顺序以及线段斜率如何,都能正确绘制。





