Symmetric Tree(DFS,二叉树的构建以及测试代码)
基础有待加强啊,由该题引发出来一些问题,现在来总结下。
首先是二叉树的结构:
struct TreeNode { EleType val; TreeNode *left; TreeNode *right; };
然后是二叉树,先序遍历的构建方法,由于只有扩展后的二叉树可以做到一个遍历序列确定一颗二叉树,比如图所示前序遍历序列(根左右)就为12#4##3##。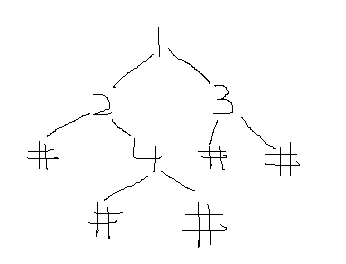
二叉树构建的代码,因为要对传递的值进行改变,所以不能值传递,所以注意这里的参数为指向TreeNode类型的指针的一个引用,
这是因为如果直接传递指针变量,给该函数的形参初始化之后,该形参在退出该函数就自动回收啦。
int CreateBiTree(TreeNode* &T) { char data; //按先序次序输入二叉树中结点的值(一个字符),‘#’表示空树 scanf("%c",&data); if(data == '#'){ T = NULL; } else{ T = (TreeNode*)malloc(sizeof(TreeNode)); T->val = data; CreateBiTree(T->left); CreateBiTree(T->right); } return 0; }
该题的思路:主要有递归和栈来实现两种方法。中心对称即左子树中某个节点的左孩子=对应的右子树的节点的右孩子,该节点的右孩子=对应结点的左孩子。
代码:
#include <iostream> #include <vector> #include <cmath> using namespace std; typedef int EleType; struct TreeNode { EleType val; TreeNode *left; TreeNode *right; }; class Solution { public: bool check(TreeNode *leftNode, TreeNode *rightNode) { if (leftNode == NULL && rightNode == NULL) return true; if (leftNode == NULL || rightNode == NULL) return false; return leftNode->val == rightNode->val && check(leftNode->left, rightNode->right) && check(leftNode->right, rightNode->left); } bool isSymmetric(TreeNode *root) { if (root == NULL) return true; return check(root->left, root->right); } }; //按先序序列创建二叉树 int CreateBiTree(TreeNode* &T){ int data; //按先序次序输入二叉树中结点的值(一个字符),‘#’表示空树 cin>>data; if(data == -1){ T = NULL; } else{ T = (TreeNode*)malloc(sizeof(TreeNode)); //生成根结点 T->val = data; //构造左子树 CreateBiTree(T->left); //构造右子树 CreateBiTree(T->right); } return 0; } int main() { freopen("C:\\Users\\Administrator\\Desktop\\test.txt","r",stdin); TreeNode* root=NULL; CreateBiTree(root); Solution so; cout<<so.isSymmetric(root)<<endl; return 0; }
ps:递归的终止条件:左节点和右节点都为空,则true;
左节点和右节点中只有一个不为空,返回false(因为上面的判断保证了肯定有一个不为空)


