Codeforces 348B：Apple Tree（DFS+LCM+思维）
http://codeforces.com/contest/348/problem/B
题意：给一棵树，每个叶子结点有w[i]个苹果，每个子树的苹果数量为该子树所有叶子结点苹果数量之和，要使得每个结点的各个子树苹果数量相等，求至少需要拿走的苹果数量。
思路：一开始以为只要使得所有子树之和相同就行了。
1 void dfs(int u, int fa) { 2 int num = 0, mi = INF; 3 for(int i = head[u]; ~i; i = edge[i].nxt) { 4 int v = edge[i].v; if(v == fa) continue; 5 dfs(v, u); 6 sz[u] += sz[v]; num++; mi = mi > sz[v] ? sz[v] : mi; 7 } 8 //printf("%d : %lld - %d - %d\n", u, sz[u], mi, num); 9 ans += sz[u] - mi * num; 10 sz[u] = mi * num + w[u]; 11 }
后来看错误的样例，是没理解好题意。
例如这组样例：
10 0 9 5 0 0 0 0 0 9 7 7 5 8 1 1 5 4 3 2 4 4 7 7 9 10 6 6 8
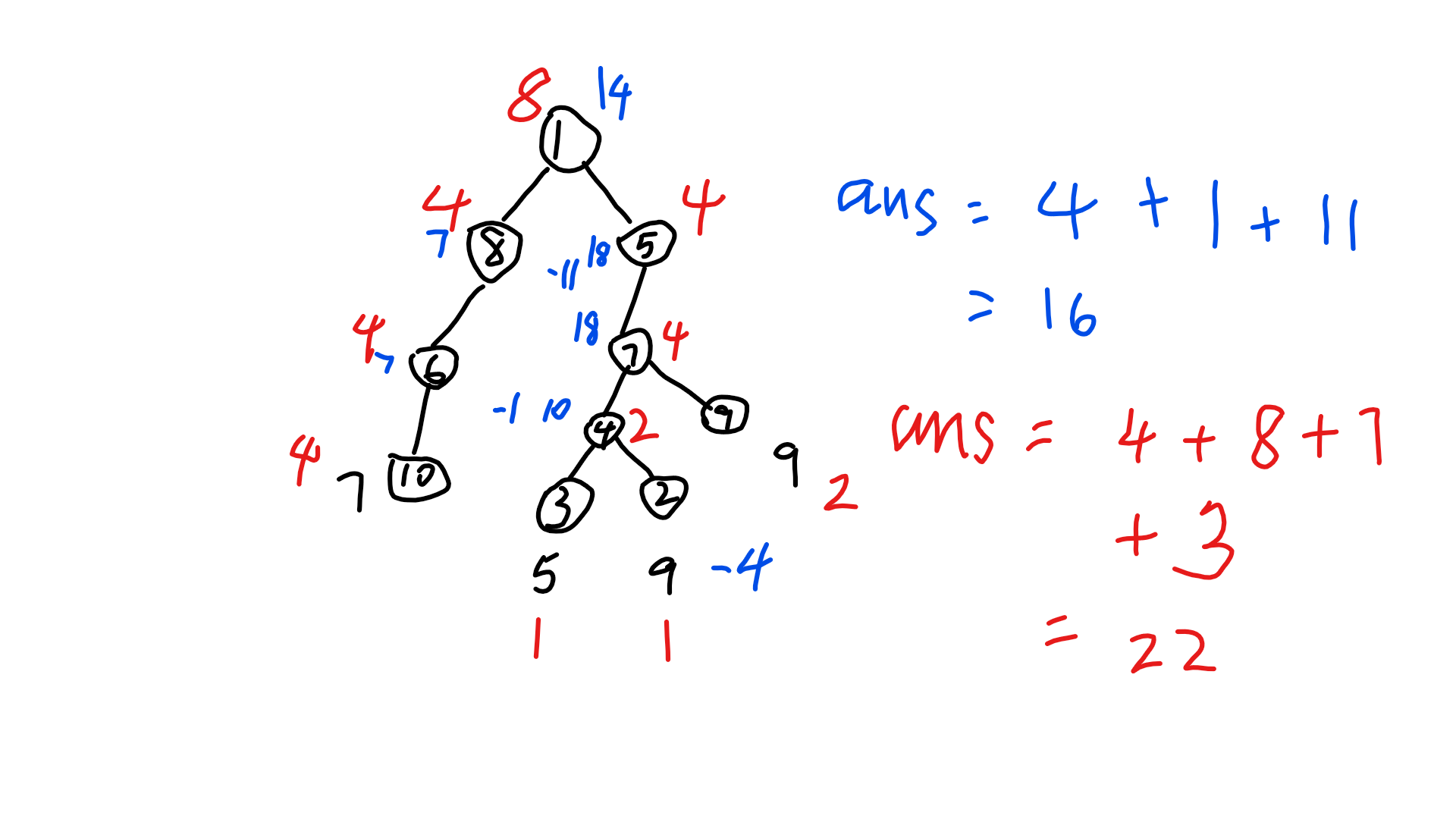红色的为正确的，蓝色为之前想错的。
题解：“对于一棵以u为根的子树，如果要减少若干个苹果，那么需要从u的每棵子树中取走等量的苹果，这个过程会递归下去直到叶子，
考虑对每个节点维护两个信息，mx[u]表示u子树中最多的苹果数，cnt[u]表示u子树中苹果数必须是cnt[u]的倍数，
如果u是叶子，那么有mx[u]=a[u]，cnt[u]=1，否则有cnt[u]=lcm(cnt[v])，这里v是u的儿子，mx[u]则是不超过min(mx[v])的最大的cnt[u]的倍数，
最后结果就是mx[1]，复杂度O(nlogA)，这个logA是gcd的复杂度。”
真的好厉害 = =
1 #include <bits/stdc++.h> 2 using namespace std; 3 typedef long long LL; 4 #define N 100010 5 #define INF 0x3f3f3f3f 6 struct Edge { 7 int v, nxt; 8 } edge[N*2]; 9 LL w[N], ans, mx[N], cnt[N]; 10 int head[N], tot; 11 void Add(int u, int v) { 12 edge[tot] = (Edge) { v, head[u] }; head[u] = tot++; 13 edge[tot] = (Edge) { u, head[v] }; head[v] = tot++; 14 } 15 16 LL gcd(LL a, LL b) { return b ? gcd(b, a % b) : a; } 17 18 LL lcm(LL a, LL b) { return a / gcd(a, b) * b; } 19 20 void dfs(int u, int fa) { 21 int num = 0; 22 for(int i = head[u]; ~i; i = edge[i].nxt) { 23 int v = edge[i].v; if(v == fa) continue; 24 dfs(v, u); 25 if(!num) mx[u] = mx[v], cnt[u] = cnt[v]; 26 else { 27 if(cnt[u] < 1e14) cnt[u] = lcm(cnt[u], cnt[v]); 28 mx[u] = min(mx[u], mx[v]) / cnt[u] * cnt[u]; // mx 必须是cnt[u]的倍数 29 } 30 num++; 31 } 32 if(!num) mx[u] = w[u], cnt[u] = 1; 33 else { 34 mx[u] *= num; 35 if(cnt[u] < 1e14) cnt[u] *= num; 36 } 37 // printf("%d : %lld - %lld\n", u, mx[u], cnt[u]); 38 } 39 40 int main() { 41 int n; scanf("%d", &n); LL ans = 0; 42 for(int i = 1; i <= n; i++) scanf("%lld", &w[i]), ans += w[i]; 43 memset(head, -1, sizeof(head)); tot = 0; 44 for(int i = 1; i < n; i++) { 45 int u, v; scanf("%d%d", &u, &v); Add(u, v); 46 } 47 dfs(1, -1); 48 cout << ans - mx[1] << endl; 49 return 0; 50 }
