【Origin】【Python】大学物理实验数据处理
摘要
大物实验的数据处理、作图、计算斜率、不确定度是否令你苦恼?在密密麻麻的坐标纸上作图是否令你感到头秃?没有关系,软件作图+数据处理一体化流程可以大大简便你的工作!
本文用到以下两个软件,任选其一即可:
- Origin:https://www.originlab.com/
- Python3(Jupyter Notebook):https://www.jianshu.com/p/62f155eb6ac5
其中Origin通用且方便计算不确定度,Python适用于有编程基础、不需要计算不确定度时。
根据已知数据点拟合
Origin
- 打开OringinPro,创建blank workbook
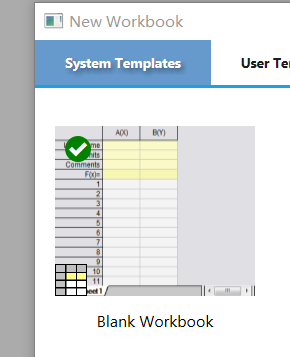
- 将已知数据点输入框,并标注变量名及单位
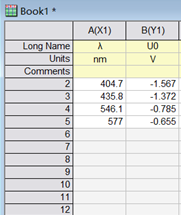
- 如果需要拟合的Y变量为Y1处理后的结果,如lnY1,可以setColumnValues直接处理
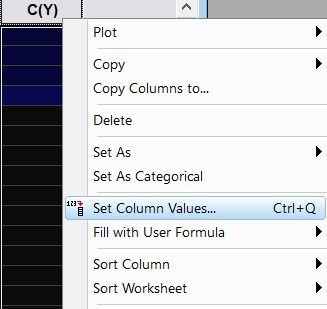

Origin公式语法很简单,不清楚的可以百度
-
选择菜单栏-plot-scatter,绘制散点,观察散点符合什么样的曲线
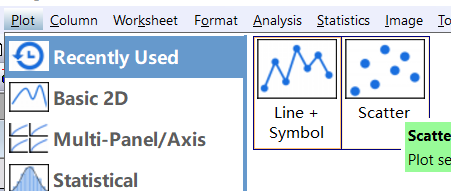
-
选择菜单栏-analysis-自己需要的拟合方式
- linear fit:线性拟合
- nonlinear curve fit:非线性拟合,可进入窗口选择所需的拟合形式。
在category中,exponential为指数拟合,logarithm为对数拟合。
选择category后,可进入function中选择具体的系数格式。
- 制定需要拟合的变量,进行拟合,图中会给出拟合函数的参数、不确定度
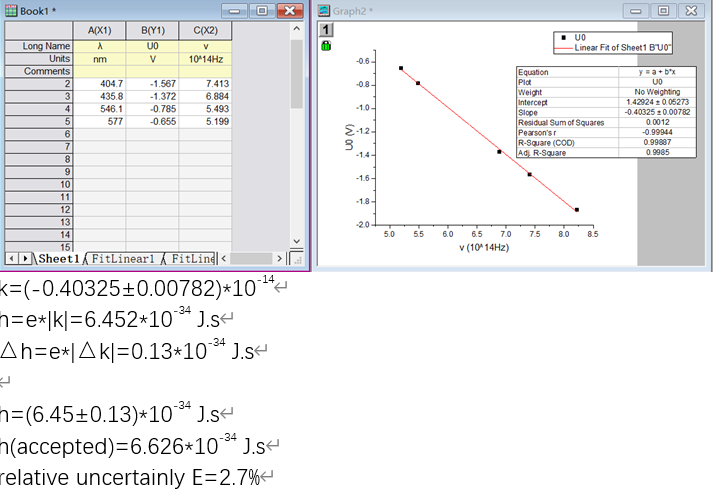
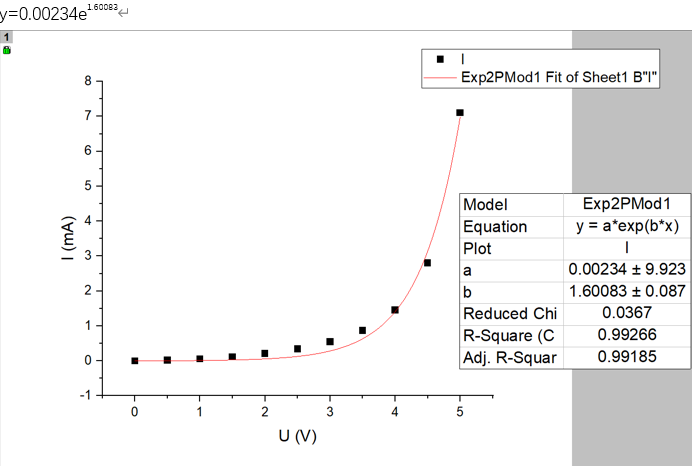
Python
线性拟合
import numpy as np
from scipy.optimize import leastsq
x=np.array([0.0,0.5,1.0,1.5,2.0,2.5,3.0,3.5,4.0,4.5,5.0,5.5])
y=np.array([0.000,0.022,0.041,0.058,0.078,0.094,0.119,0.138,0.155,0.175,0.192,0.213])
def residuals(p):
"计算以p为参数的直线和原始数据误差"
k,b=p#若不是线性拟合,则修改对应参数
return y-(k*x+b)
#leastsq使residuals()输出数组的平方和最小,初值[1,0]
r=leastsq(residuals,[1,0])#若不是线性拟合,则修改对应参数
k,b=r[0]#若不是线性拟合,则修改对应参数
x1=np.arange(0.00,5.50,0.01)
y1=k*x1+b#若不是线性拟合,则修改对应参数
print("k=",k,"b=",b)#若不是线性拟合,则修改对应参数
#画图
import matplotlib.pyplot as plt
plt.scatter(x,y,c='g',label='scatter')#散点图
plt.plot(x1,y1,'b',label='fitting')
plt.title('半桥电路')
plt.xlabel('△X')
plt.ylabel('△V')
plt.legend()#显示标签
plt.show()
输出:
k= 0.03846853146643514 b= 0.0012948717948720755
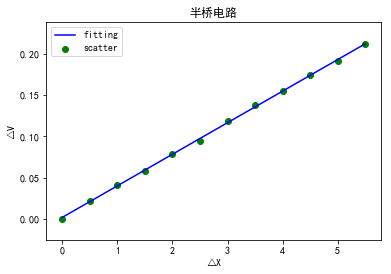
非线性拟合
若使用其他函数进行拟合,只需将k*x+b替换为对应和函数(参数)即可。
两曲线画在一张图中
只需修改两段代码的变量名称,绘图时scatter/plot两次:
#画图
import matplotlib.pyplot as plt
plt.scatter(x2,y2,c='b',label='全桥散点')#散点图
plt.plot(x1,y1,'b',label='全桥拟合')
plt.scatter(x,y,c='r',label='半桥散点')#散点图
plt.plot(x3,y3,'r',label='半桥拟合')
plt.title('两电路△V-△X图像')
plt.xlabel('△X')
plt.ylabel('△V')
plt.legend()#显示标签
plt.show()
输出:
k= 0.09064835176318456 b= 0.007285713826015861
k= 0.03846853146643514 b= 0.0012948717948720755
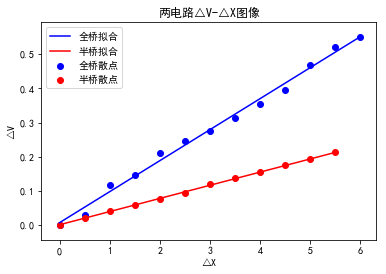
连接数据点作平滑曲线
Origin
https://jingyan.baidu.com/article/f7ff0bfc1b47372e26bb133a.html
Python
同样用到B-样条插值。
输入:
import numpy as np
import matplotlib.pyplot as plt
#进行样条插值
import scipy.interpolate as spi
plt.rcParams['font.sans-serif']=['SimHei'] #用来正常显示中文标签
plt.rcParams['axes.unicode_minus']=False #用来正常显示负号
#数据准备
X=[15.1,17.1,19.1, 19.4,21.4,23.4, 25.6,27.6,29.6, 30.6,32.6,34.6, 37.0,39.0,41.0, 42.5,44.5,46.5, 49.2,51.2,53.2, 54.7,56.7,58.7, 61.8,63.8,65.8, 67.6,69.6,71.6, 75.2,77.2,79.2, 81.2,83.2,85.2]
Y=[175,213,179, 176,87,178, 298,340,272, 171,43,168, 345,407,332, 159,24,158, 399,466,371, 210,57,164, 433,517,437, 250,144,229, 518,588,505, 369,307,379]
#定义插值点
ix3=np.arange(15.1,85.2,0.1)
#进行三次样条拟合
ipo3=spi.splrep(X,Y,k=3) #样本点导入,生成参数
iy3=spi.splev(new_x,ipo3) #根据观测点和样条参数,生成插值
#作图
plt.plot(X,Y,'o',ix3,iy3)
plt.xlabel('Vp/V')
plt.ylabel('IA/μA')
plt.title('弗兰克-赫兹图')
plt.show()
输出:
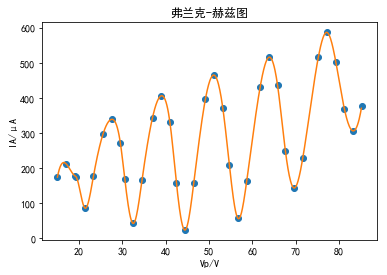


 浙公网安备 33010602011771号
浙公网安备 33010602011771号