【LaTex】LaTex论文排版入门+速成

摘要

无脑LaTex教程，采用texlive+texworks/自选编辑器+XeLaTex，上手就能用，可以满足个人撰写文档的基本需求。如果有更高要求或文中没有提到的内容，通过百度可以解决一切。
本文仅适用于Windows用户，Mac用户请到文末参考资料中寻找对应教程。
LaTex很好上手！不要畏难哦~

下载和安装

使用

  • ...：LaTex使用\作为标识，表示对应的功能。
  • %：表示注释，其后的内容不被编译
  • 如果需要打出'_','%','^'等功能性字符，在这些字符前加''即可
    将每一个模块撰写完成后，选择排版工具为“XeLaTex”，单击左上角的开始绿三角，则会在当前文件夹编译出pdf文档。

模块

撰写LaTex源码时，可将其分为三个模块。

“头文件”

以下是一个简单的范例：

%使之适用中文
\documentclass[UTF8]{ctexart}

%\usepackage为调用所需的包，用到哪个功能就要在这里添加对应的包
\usepackage{graphicx}
\usepackage{geometry}
\usepackage{multirow}
\usepackage{booktabs}
\usepackage[fleqn]{amsmath}

%纸张规格，scale=''意为文档文字部分占整个纸张的比例
\geometry{a4paper,scale=0.75}

%标题
\title{葡萄酒质量评价数据分析}
%作者
\author{Y.X.Sun}
%日期
\date{\today}
\begin{document}
%添加目录
\maketitle
\tableofcontents

正文

和markdown一样，latex有一级、二级……n级标题：

\section{一级标题}
\subsection{二级标题}
\subsubsection{三级标题}

在每个部分，都可以随意的插入段落。但我们有更好的段落插入方法：

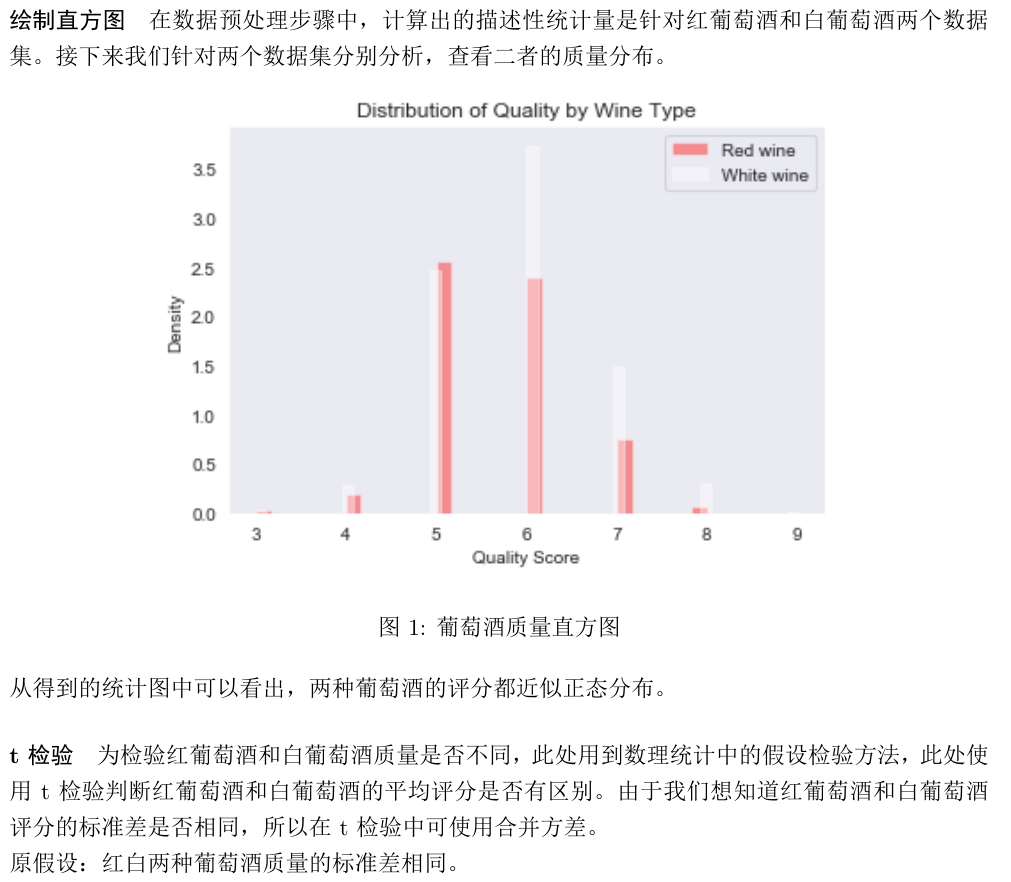
\paragraph{绘制直方图}在数据预处理步骤中，计算出的描述性统计量是针对红葡萄酒和白葡萄酒两个数据集。接下来我们针对两个数据集分别分析，查看二者的质量分布。
\paragraph{t检验}为检验红葡萄酒和白葡萄酒质量是否不同，此处用到数理统计中的假设检验方法，此处使用t检验判断红葡萄酒和白葡萄酒的平均评分是否有区别。由于我们想知道红葡萄酒和白葡萄酒评分的标准差是否相同，所以在t检验中可使用合并方差。

效果：
avatar

“尾文件”

通常情况下，结束只需要：

\end{document}

此处是开头\begin{document}的补全，千万不要忘记，否则会出现一直编译不出来的情况。

具体方法

换行、空格

  • 换行：两次enter
  • 空格：\quad

图片

\begin{figure}[h]
    \centering
    \includegraphics[width=0.7\textwidth]{图片名称.png}
    \caption{显示出来的图片名称}
    \label{pic1}
\end{figure}

公式

$abc$代表公式嵌入行内
$$abc$$代表公式单独一行

参考资料：https://zhuanlan.zhihu.com/p/110756681

表格

可以参考表格生成器进行编辑：https://zhuanlan.zhihu.com/p/62317790

参考文献

简略方法：

\begin{thebibliography}{99}  
\bibitem{ref1}Clinton W.Brownley. Foundations for Analysis with Python  
\bibitem{ref2}现代密码学教程. 谷利泽,郑世慧,杨义先．北京邮政大学出版社. 2009
\bibitem{ref5}推荐系统中的算法[J]. 黄茂洲. 科技风. 2019(01).
\bibitem{ref3}https://www.zhihu.com/question/397159736
\bibitem{ref4}https://baike.baidu.com/item/%E7%94%9F%E6%97%A5%E6%82%96%E8%AE%BA
\end{thebibliography}
\end{document}

效果：
avatar

总结

我的文章[https://www.cnblogs.com/fighterkaka22/p/14100517.html]被编译为LaTex后：

\documentclass[UTF8]{ctexart}
\usepackage{graphicx}
\usepackage{geometry}
\usepackage{multirow}
\usepackage{booktabs}
\usepackage[fleqn]{amsmath}
\geometry{a4paper,scale=0.75}
\title{葡萄酒质量评价数据分析}
\author{Y.X.Sun}
\date{\today}
\begin{document}
\maketitle
\tableofcontents
\setlength{\parindent}{0pt}
\section{概述}
本例为演示数据分析的流程和对概率论和数理统计基础知识的应用，使用Python的pandas和statmodels生成标准的描述性统计量和模型，对数据集进行探索和摘要分析，并利用多元线性回归进行回归分析。

本例以葡萄酒类型为标签，分为白葡萄酒和红葡萄酒。比较这两种葡萄酒的差别并选取葡萄酒的化学成分：固定酸度、挥发性酸度、柠檬酸、氯化物、游离二氧化硫、总硫度、密度、PH值、硫酸盐、酒精度数共11个，针对酒的各类化学成分建立线性回归模型，从而预测该葡萄酒的质量评分。

应用到数理统计知识点：随机变量标准化，随机变量数字特征，正态分布，假设检验，线性回归
\section{数据收集和预处理}
数据集来源：UCI Machine Learning Repository

首先进行数据预处理和数据描述性统计，其中描述性统计量包括总数、均值、标准差、最小值、第25个百分位数、中位数、第75个百分位数和最大值。

经过对各描述性统计量知，没有缺失值和异常值，不需进行补充和处理。
\section{数据分析}
\subsection{分组、直方图和t检验}
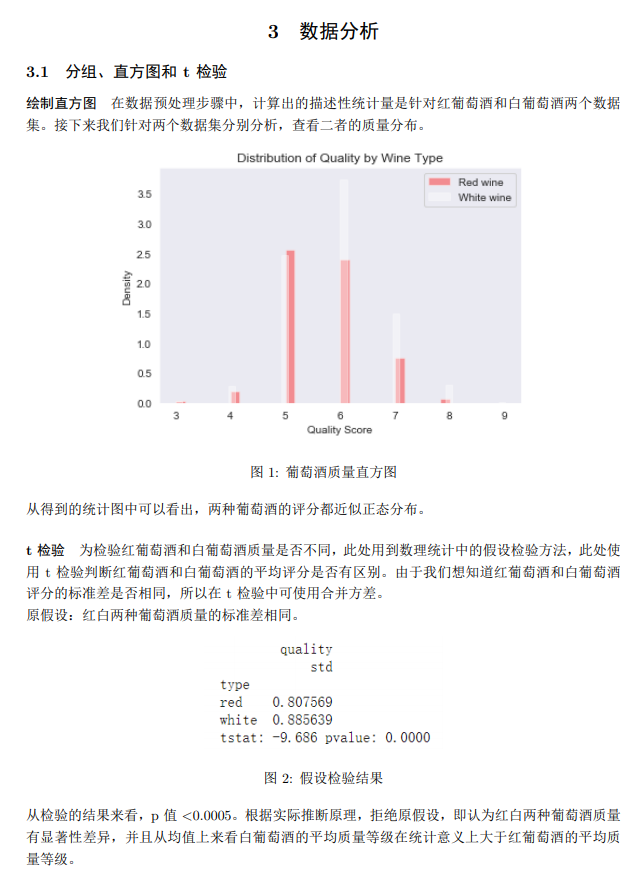
\paragraph{绘制直方图}在数据预处理步骤中，计算出的描述性统计量是针对红葡萄酒和白葡萄酒两个数据集。接下来我们针对两个数据集分别分析，查看二者的质量分布。
\begin{figure}[h]
    \centering
    \includegraphics[width=0.7\textwidth]{QualityScore.png}
    \caption{葡萄酒质量直方图}
    \label{pic1}
\end{figure}

从得到的统计图中可以看出，两种葡萄酒的评分都近似正态分布。
\paragraph{t检验}为检验红葡萄酒和白葡萄酒质量是否不同，此处用到数理统计中的假设检验方法，此处使用t检验判断红葡萄酒和白葡萄酒的平均评分是否有区别。由于我们想知道红葡萄酒和白葡萄酒评分的标准差是否相同，所以在t检验中可使用合并方差。

原假设：红白两种葡萄酒质量的标准差相同。
\begin{figure}[h]
    \centering
    \includegraphics[width=0.4\textwidth]{假设检验结果.png}
    \caption{假设检验结果}
    \label{pic2}
\end{figure}

从检验的结果来看，p值<0.0005。根据实际推断原理，拒绝原假设，即认为红白两种葡萄酒质量有显著性差异，并且从均值上来看白葡萄酒的平均质量等级在统计意义上大于红葡萄酒的平均质量等级。
\subsection{变量关系和相关性}接下来我们研究一下变量之间的相关性，并创建部分变量之间带有回归直线的散点图。数据集中有6000多个点，如果将它们都画在统计图中，就很难分辨出清楚的点。因此我们使用take\_sample函数进行抽样。
\begin{figure}[h]
    \centering
    \includegraphics[width=0.9\textwidth]{相关性.png}
    \caption{相关性}
    \label{pic3}
\end{figure}
从各变量的相关系数来看酒精含量、硫酸酯、pH 值、游离二氧化硫和柠檬酸这些指标与质量呈现正相关，即当这些指标的含量增加时，葡萄酒的质量会提高；非挥发性酸、挥发性酸、残余糖分、氯化物、总二氧化硫和密度这些指标与质量呈负相关即当这些指标的含量增加时，葡萄酒的质量会降低。从相关系数可以看出，对葡萄酒质量影响最大的是葡萄酒是酒精含量，其相关系数为0.444，其次是酒的密度，但酒的密度对酒的质量是负影响的。
\subsection{最小二乘法线性回归}
\paragraph{系数解释}
相关系数和两两变量之间的统计图有助于对两个变量之间的关系进行量化和可视化。但它们不能测量出每个自变量在其他自变量不变时与因变量之间的关系，线性回归可以解决这个问题。

线性回归模型如下：
$$ y_i\sim N(\mu_i,\sigma^2) $$
$$ \mu_i=\beta_0+\beta_1x_{i1}+\beta_2x_{i2}+\cdots+\beta_px_{ip} $$
这个模型表示观测$y_i$服从均值为$ \mu_i $方差为$ \sigma^2 $的正态分布，其中$\mu_i$依赖于自变量，$ \sigma^2 $为一个常数。也就是说，给定了自变量的值以后，我们就可以得到一个具体的质量评分，但在另一天，给定同样的自变量值，我们可能会得到一个与前面不同的质量评分。但经过一个较长的周期，质量评分会落在$ \mu\pm\sigma $这个范围内。
\paragraph{自变量标准化}
关于这个模型，还需要注意的一点是，普通最小二乘回归是通过使残差平方和最小化来估计未知的β参数值。由于残差大小依赖于自变量的测量单位。所以当自变量测量单位不同，我们需要将自变量标准化。
$$ Z\sim\frac{X-\mu}{\sigma} $$
由上一步的观测数据知，各变量间最大值和最小值之间差别很大，因此应进行标准化。

pandas在数据框中对变量进行标准化非常容易。你可以对一个观测写一个变换公式，pandas将其扩展到行和列中，来标准化所有变量。
\begin{figure}[h]
    \centering
    \includegraphics[width=0.9\textwidth]{result.png}
    \caption{线性回归结果}
    \label{pic4}
\end{figure}

观测标准化后的数据知，线性回归模型为：
\begin{equation}
\begin{split}
quality= 0.0877fixed acidity -0.2186volatile acidity -0.0159citric\_acid+ 0.2072residual\_sugar\\
-0.0169chlorides+ 0.1060free\_sulfur\_dioxide -0.1648density-0.1402total\_sulfur\_dioxide\\
+0.0706pH+0.1143sulphates+ 0.3185alcohol+5.8184
\end{split}
\end{equation}

在我们的模型摘要中，截距系数的意义就是当一种葡萄酒的所有成分都取均值时，它的质量评分均值应该是5.8，标准差为0.009。
\subsection{预测}
有了线性回归模型，当给出了葡萄酒的化学成分的数据就可以预测该葡萄酒的质量评分。
\end{document}

效果：
avatar
avatar
avatar

参考资料

posted @ 2020-12-08 22:02  盐析Yuki  阅读(715)  评论(2)  编辑  收藏  举报
// 侧边栏目录 // https://blog-static.cnblogs.com/files/douzujun/marvin.nav.my1502.css