【Python】常用数值方法的python实现
目录
解非线性方程
方法综述
- 使用SymPy符号计算库中的solve()(解析解)/nsolve()(数值解)函数。
- 一元方程数值解可使用迭代法辅助求解。
问题分类
求解一元方程
问题引入:求该方程数值解
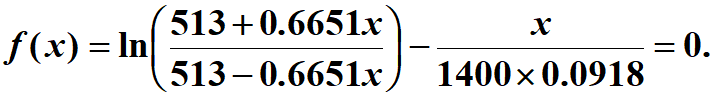
解法一:SymPy.solve/nsolve函数求解
实际上SymPy内置解方程方法为迭代法。
输入:
import numpy as np
from sympy import *
var("x")
#方法一:求解解析解,进一步得出数值解
#solve()参数:表达式,自变量
result1=solve(x**3-x-1,x)
#求出解析解后,可根据解析解找出所需要的解,evalf()输出数值解
result1[2].evalf()
#方法二:对于没有解析解的方程,直接输出数值解
result2=nsolve(ln((513+0.6651*x)/(513-0.6651*x))-x/(1400*0.0918),0)
result2
输出:
1.32471795724475
0
解法二:迭代法
本方法仅提供一种思路,实际求解时可直接用解法一。实际上SymPy内置解方程方法为迭代法。
示例:双点弦截法
输入:
#解方程法二:迭代法
#方法一:弦截法
import numpy as np
import matplotlib.pyplot as plt
#可以显示中文
plt.rcParams["font.sans-serif"] = ["SimHei"]
plt.rcParams['axes.unicode_minus'] = False
# 设置风格
plt.style.use('ggplot')
# 定义函数
init_fun = lambda x: (513+0.6651*x)/(513-0.6651*x)-x/(1400*0.0918)
# 导数
#deri_fun = lambda x: 2*x-4
# input
'''
x0:初始值1
x1:初始值2
theta:误差上界
'''
x0=float(input('输入初始点x0:较大值\n'))
x1=float(input('输入初始点x1:较小值\n'))
theta=1e-7
fig_1 = plt.figure(figsize = (8, 6))
plt.hlines(0,-1,x0,'black','--')
plt.xlabel('X')
plt.ylabel('Y')
plt.title('函数图像')
# 函数图像
x=[]
if x0>0:
x = np.arange(-1,x0,0.05)
plt.hlines(0,-1,x0,'black','--')
else:
x = np.arange(x0,10,0.05)
plt.hlines(0,x0,10,'black','--')
y = init_fun(x)
def Secant(func = init_fun, x0 =x0, x1 = x1, theta = theta):
number=0
while True:
x2=x0-func(x0)*(x1-x0)/(func(x1)-func(x0))
plt.vlines(x0,0,init_fun(x0),'blue','--')
plt.plot([x2,x0],[0,func(x0)],'r--',c='green')
plt.scatter(x0,func(x0),c='black')
if abs(func(x2))<theta:
return x2,number
x0=x1
x1=x2
number += 1
# 迭代法计算求解x0
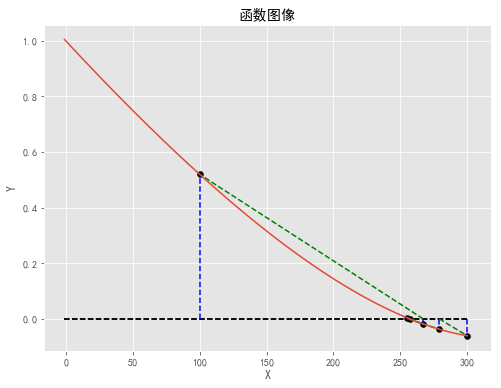
xi,number = Secant(init_fun, x0, x1, theta)
print('迭代结果:'+str(xi))
print('迭代次数:'+str(number))
## 函数求解
plt.plot(x,y)
plt.show()
输出:
输入初始点x0:较大值
300
输入初始点x1:较小值
100
迭代结果:256.84798935747875
迭代次数:5
如果希望在lambda表达式输入对数、指数操作,只需引用np:
# 定义函数
init_fun = lambda x: np.log((513+0.6651*x)/(513-0.6651*x))-x/(1400*0.0918)
求解多元方程组
与求解一元方程同理。
方法一:运用SymPy
输入:
import numpy as np
from sympy import *
var("x,y")
#方法一:求解解析解,进一步得出数值解
#solve()参数:表达式,变量
result1=solve((x**2+x*y+1,y**2+x*y+2),x,y)
result1
#求出解析解后,可根据解析解找出所需要的解,evalf()输出数值解
result1[0][0].evalf()
#方法二:对于没有解析解的方程,直接输出数值解
var("x,y")
f1=x**2+y*x-1
f2=y**2+x+2
#初值要选好,否则会迭代不收敛
nsolve((f1,f2),(x,y),(I,I))
输出:
[(-sqrt(3)*I/3, -2*sqrt(3)*I/3), (sqrt(3)*I/3, 2*sqrt(3)*I/3)]
-0.577350269189626*I
Matrix([
[0.518912794385156 - 0.666609844932019*I],
[ 0.208223290106041 + 1.60070913439255*I]])
方法二:运用SciPy.optimize.fsolve()
输入:
from scipy.optimize import fsolve
from math import sin
def f(x):
x0,x1,x2=x.tolist()
return[
5*x1+3,
4*x0*x0-2*sin(x1*x2),
x1*x2-1.5
]
#f计算方程组误差,[1,1,1]是初值
result=fsolve(f,[1,1,1])
print(result)
print(f(result))
输出:
[-0.70622057 -0.6 -2.5 ]
[0.0, -9.126033262418787e-14, 5.329070518200751e-15]
解线性方程组
方法:使用scipy.linalg的solve()方法
输入:
import numpy as np
from scipy.linalg import solve
a = np.array([[3, 1, -2], [1, -1, 4], [2, 0, 3]])
b = np.array([5, -2, 2.5])
x = solve(a, b)
x
输出:
array([0.5, 4.5, 0.5])
插值法
方法综述
插值是一种通过已知的离散数据来求未知数据的方法。与拟合不同的是,它要求曲线通过所有的已知数据。SciPy的interpolate模块提供了许多进行插值运算的函数。
问题分类
一元函数插值
其他插值方法的Python实现可参考:http://liao.cpython.org/scipy11/
文档仅演示最常用的B样条插值。
B样条插值
方法一:interp1d()
一维数据的B样条插值运算可以通过interp1d()完成。
interp1d(x,y,kind='cubic')
参数x和y:一系列已知的数据点。
kind:插值类型。
- 'zero','nearest':阶梯插值,相当于0阶B样条曲线。
- 'slinear','linear':线性插值,相当于1阶B样条曲线。
- 'quadratic','cubic':2阶和3阶B样条曲线,更高阶的曲线可直接使用整数值指定。
实际常用三次B样条插值。
输入:(数据来源于本人物理实验BII弗兰克-赫兹实验数据)
#绘图工具:pylab
import numpy as np
from scipy import interpolate
import pylab as pl
x=[15.1,17.1,19.1, 19.4,21.4,23.4, 25.6,27.6,29.6, 30.6,32.6,34.6, 37.0,39.0,41.0, 42.5,44.5,46.5, 49.2,51.2,53.2, 54.7,56.7,58.7, 61.8,63.8,65.8, 67.6,69.6,71.6, 75.2,77.2,79.2, 81.2,83.2,85.2]
y=[175,213,179, 176,87,178, 298,340,272, 171,43,168, 345,407,332, 159,24,158, 399,466,371, 210,57,164, 433,517,437, 250,144,229, 518,588,505, 369,307,379]
xnew=np.arange(15.1,85.2,0.1)
pl.plot(x,y,"ro")
for kind in ["cubic"]:#插值方式
#"nearest","zero"为阶梯插值
#slinear 线性插值
#"quadratic","cubic" 为2阶、3阶B样条曲线插值
f=interpolate.interp1d(x,y,kind=kind)
# ‘slinear’, ‘quadratic’ and ‘cubic’ refer to a spline interpolation of first, second or third order)
ynew=f(xnew)
pl.plot(xnew,ynew,label=str(kind))
pl.legend(loc="lower right")
pl.show()
输出:
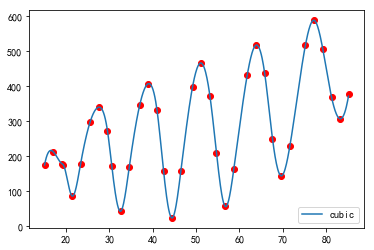
与示波器输出的图像十分类似。

方法二:splrep()+splev()
该函数可以找到一维曲线的B-spline表示。
输入:
import numpy as np
import matplotlib.pyplot as plt
#进行样条插值
import scipy.interpolate as spi
plt.rcParams['font.sans-serif']=['SimHei'] #用来正常显示中文标签
plt.rcParams['axes.unicode_minus']=False #用来正常显示负号
#数据准备
X=[15.1,17.1,19.1, 19.4,21.4,23.4, 25.6,27.6,29.6, 30.6,32.6,34.6, 37.0,39.0,41.0, 42.5,44.5,46.5, 49.2,51.2,53.2, 54.7,56.7,58.7, 61.8,63.8,65.8, 67.6,69.6,71.6, 75.2,77.2,79.2, 81.2,83.2,85.2]
Y=[175,213,179, 176,87,178, 298,340,272, 171,43,168, 345,407,332, 159,24,158, 399,466,371, 210,57,164, 433,517,437, 250,144,229, 518,588,505, 369,307,379]
#定义插值点
ix3=np.arange(15.1,85.2,0.1)
#进行三次样条拟合
ipo3=spi.splrep(X,Y,k=3) #样本点导入,生成参数
iy3=spi.splev(new_x,ipo3) #根据观测点和样条参数,生成插值
#作图
plt.plot(X,Y,'o',ix3,iy3)
plt.xlabel('Vp/V')
plt.ylabel('IA/μA')
plt.title('弗兰克-赫兹图')
plt.show()
输出:
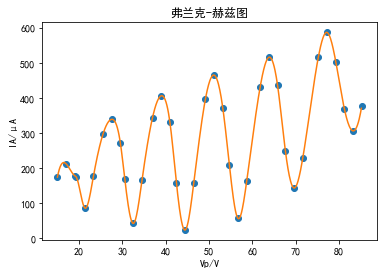
二元函数插值
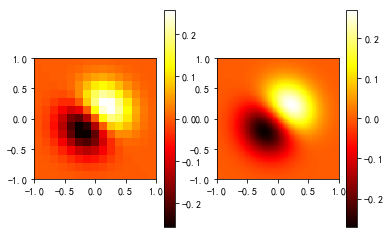
绘制2D图
输入:
# -*- coding: utf-8 -*-
import numpy as np
from scipy import interpolate
import pylab as pl
import matplotlib as mpl
def func(x, y):
return (x+y)*np.exp(-5.0*(x**2 + y**2))
# X-Y轴分为15*15的网格
y,x= np.mgrid[-1:1:15j, -1:1:15j]
fvals = func(x,y) # 计算每个网格点上的函数值 15*15的值
print(len(fvals[0]))
#三次样条二维插值
newfunc = interpolate.interp2d(x, y, fvals, kind='cubic')
# 计算100*100的网格上的插值
xnew = np.linspace(-1,1,100)#x
ynew = np.linspace(-1,1,100)#y
fnew = newfunc(xnew, ynew)#仅仅是y值 100*100的值
# 输出解得所求点的插值
print(newfunc(0.01,0.01))
# 绘图
# 为了更明显地比较插值前后的区别,使用关键字参数interpolation='nearest'
# 关闭imshow()内置的插值运算。
pl.subplot(121)
im1=pl.imshow(fvals, extent=[-1,1,-1,1], cmap=mpl.cm.hot, interpolation='nearest', origin="lower")#pl.cm.jet
#extent=[-1,1,-1,1]为x,y范围 favals为
pl.colorbar(im1)
pl.subplot(122)
im2=pl.imshow(fnew, extent=[-1,1,-1,1], cmap=mpl.cm.hot, interpolation='nearest', origin="lower")
pl.colorbar(im2)
pl.show()
输出:
15
[0.01985751]
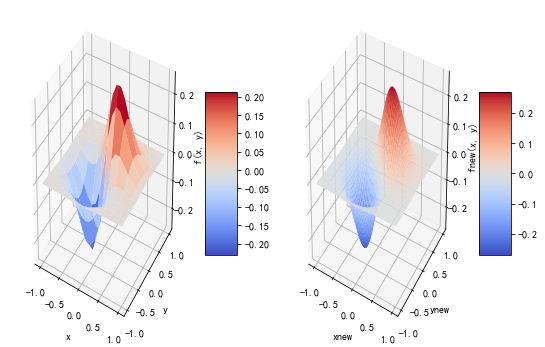
绘制3D图
输入:
# -*- coding: utf-8 -*-
"""
演示二维插值。
"""
# -*- coding: utf-8 -*-
import numpy as np
from mpl_toolkits.mplot3d import Axes3D
import matplotlib as mpl
from scipy import interpolate
import matplotlib.cm as cm
import matplotlib.pyplot as plt
def func(x, y):
return (x+y)*np.exp(-5.0*(x**2 + y**2))
# X-Y轴分为20*20的网格
x = np.linspace(-1,1,20)
y = np.linspace(-1,1,20)
x, y = np.meshgrid(x, y)#20*20的网格数据
fvals = func(x,y) # 计算每个网格点上的函数值 15*15的值
fig = plt.figure(figsize=(9, 6))
#Draw sub-graph1
ax=plt.subplot(1, 2, 1,projection = '3d')
surf = ax.plot_surface(x, y, fvals, rstride=2, cstride=2, cmap=cm.coolwarm,linewidth=0.5, antialiased=True)
ax.set_xlabel('x')
ax.set_ylabel('y')
ax.set_zlabel('f(x, y)')
plt.colorbar(surf, shrink=0.5, aspect=5)#标注
#二维插值
newfunc = interpolate.interp2d(x, y, fvals, kind='cubic')#newfunc为一个函数
# 计算100*100的网格上的插值
xnew = np.linspace(-1,1,100)#x
ynew = np.linspace(-1,1,100)#y
fnew = newfunc(xnew, ynew)#仅仅是y值 100*100的值 np.shape(fnew) is 100*100
xnew, ynew = np.meshgrid(xnew, ynew)
# 输出解得所求点的插值
print(newfunc(0.01,0.01))
# 绘制3D图
ax2=plt.subplot(1, 2, 2,projection = '3d')
surf2 = ax2.plot_surface(xnew, ynew, fnew, rstride=2, cstride=2, cmap=cm.coolwarm,linewidth=0.5, antialiased=True)
ax2.set_xlabel('xnew')
ax2.set_ylabel('ynew')
ax2.set_zlabel('fnew(x, y)')
plt.colorbar(surf2, shrink=0.5, aspect=5)#标注
plt.show()
输出:
[0.01983083]
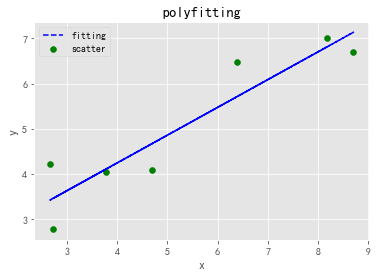
函数逼近(拟合)
最常用方法:最小二乘拟合
输入:
import numpy as np
from scipy.optimize import leastsq
x=np.array([8.19,2.72,6.39,8.71,4.7,2.66,3.78])
y=np.array([7.01,2.78,6.47,6.71,4.1,4.23,4.05])
def residuals(p):
"计算以p为参数的直线和原始数据误差"
k,b=p#若不是线性拟合,则修改对应参数
return y-(k*x+b)
#leastsq使residuals()输出数组的平方和最小,初值[1,0]
r=leastsq(residuals,[1,0])#若不是线性拟合,则修改对应参数
k,b=r[0]#若不是线性拟合,则修改对应参数
x1=np.arange(2.66,8.71,0.01)
y1=k*x+b#若不是线性拟合,则修改对应参数
print("k=",k,"b=",b)#若不是线性拟合,则修改对应参数
#画图
import matplotlib.pyplot as plt
plt.scatter(x,y,c='g',label='scatter')#散点图
plt.plot(x1,y1,'b--',label='fitting')
plt.title('polyfitting')
plt.xlabel('x')
plt.ylabel('y')
plt.legend()#显示标签
plt.show()
输出:
k= 0.6134953491930442 b= 1.794092543259387
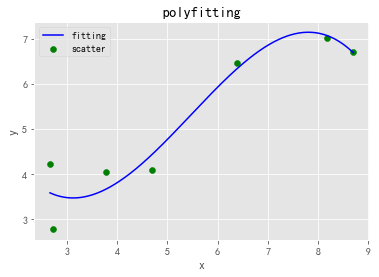
计算误差曲面函数:
def S(k,b):
#计算直线y=k*x+b与原始数据x,y误差的平方和
error=np.zeros(k,shape)
for x,y in zip(x,y)
error+=(y-(k*x+b))**2
return error
若使用其他函数进行拟合,只需将k*x+b替换为对应和函数(参数)即可。
如,三次多项式拟合图像如下:
微分方程数值解法
常微分方程
方法一:SymPy.dsolve()
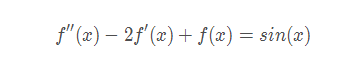
输入:
import numpy as np
from sympy import *
f = Function('f')
x = symbols('x')
eq = Eq(f(x).diff(x, x) - 2*f(x).diff(x) + f(x), sin(x))
print(dsolve(eq, f(x)))
输出:
Eq(f(x), (C1 + C2*x)*exp(x) + cos(x)/2)
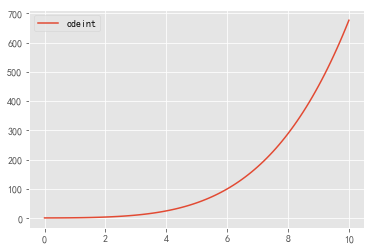
方法二:scipy.integrate.odeint()
这个函数,要求微分方程必须化为标准形式,即
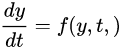
输入:
import math
import numpy as np
from scipy.integrate import odeint
import matplotlib.pyplot as plt
def func(y, t):
return t * math.sqrt(y)
YS=odeint(func,y0=1,t=np.arange(0,10.1,0.1))
t=np.arange(0,10.1,0.1)
plt.plot(t, YS, label='odeint')
plt.legend()
plt.show()
输出:
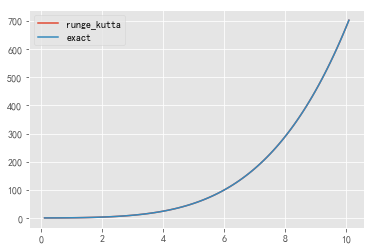
方法三:单个函数四阶龙格-库塔法
输入:
import math
import numpy as np
import matplotlib.pyplot as plt
def runge_kutta(y, x, dx, f):
""" y is the initial value for y
x is the initial value for x
dx is the time step in x
f is derivative of function y(t)
"""
k1 = dx * f(y, x)
k2 = dx * f(y + 0.5 * k1, x + 0.5 * dx)
k3 = dx * f(y + 0.5 * k2, x + 0.5 * dx)
k4 = dx * f(y + k3, x + dx)
return y + (k1 + 2 * k2 + 2 * k3 + k4) / 6.
if __name__=='__main__':
t = 0.
y = 1.
dt = .1
ys, ts = [], []
def func(y, t):
return t * math.sqrt(y)
while t <= 10:
y = runge_kutta(y, t, dt, func)
t += dt
ys.append(y)
ts.append(t)
exact = [(t ** 2 + 4) ** 2 / 16. for t in ts]
plt.plot(ts, ys, label='runge_kutta')
plt.plot(ts, exact, label='exact')
plt.legend()
#plt.show()
输出:
方法四:多个微分方程:欧拉法
输入:
import numpy as np
"""
移动方程:
t时刻的位置P(x,y,z)
steps:dt的大小
sets:相关参数
"""
def move(P, steps, sets):
x, y, z = P
sgima, rho, beta = sets
# 各方向的速度近似
dx = sgima * (y - x)
dy = x * (rho - z) - y
dz = x * y - beta * z
return [x + dx * steps, y + dy * steps, z + dz * steps]
# 设置sets参数
sets = [10., 28., 3.]
t = np.arange(0, 30, 0.01)
# 位置1:
P0 = [0., 1., 0.]
P = P0
d = []
for v in t:
P = move(P, 0.01, sets)
d.append(P)
dnp = np.array(d)
# 位置2:
P02 = [0., 1.01, 0.]
P = P02
d = []
for v in t:
P = move(P, 0.01, sets)
d.append(P)
dnp2 = np.array(d)
"""
画图
"""
from mpl_toolkits.mplot3d import Axes3D
import matplotlib.pyplot as plt
fig = plt.figure()
ax = Axes3D(fig)
ax.plot(dnp[:, 0], dnp[:, 1], dnp[:, 2])
ax.plot(dnp2[:, 0], dnp2[:, 1], dnp2[:, 2])
plt.show()
输出:
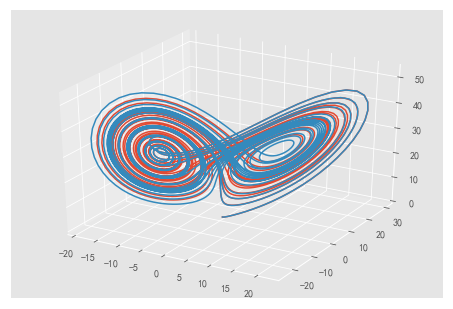
偏微分方程
与解常微分方程原理相同。
参考链接
- 《Python科学计算》-张若愚
- SymPy.solve()官方文档:https://docs.sympy.org/latest/tutorial/solvers.html
- SciPy.interpolate.splrep()官方文档(英文版):https://docs.scipy.org/doc/scipy-0.19.0/reference/generated/scipy.interpolate.splrep.html
- SciPy.interpolate.splrep()官方文档(中文版):https://vimsky.com/examples/usage/python-scipy.interpolate.splrep.html
- Python.SciPy实现Hermite插值:http://liao.cpython.org/scipy13/
- 常微分方程数值解:Python求解:https://www.jianshu.com/p/8d3671f9148d
- 微分方程在物理学中的应用:https://zhuanlan.zhihu.com/p/81488678
https://zhuanlan.zhihu.com/p/164627678


 浙公网安备 33010602011771号
浙公网安备 33010602011771号