坐标力扣:

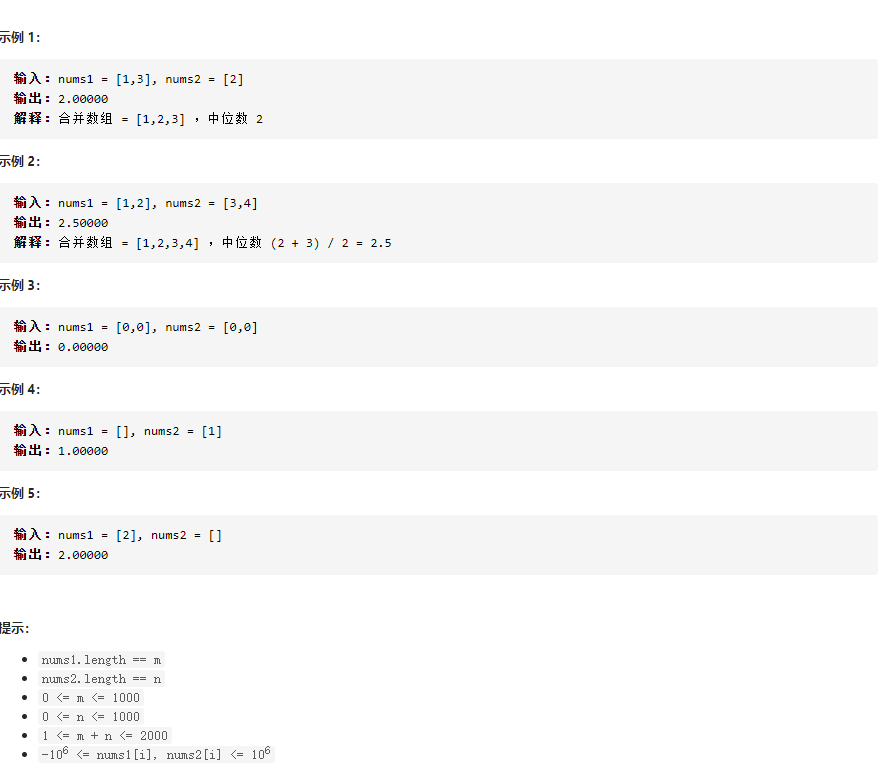
曾经做这题时,卡了我很长时间。现在故地重游,仍然重蹈覆辙。
所以我很有必要记录下这条题目。
要达到如题的时间复杂度,不难想到,所用的方法一定和二分法有关系。
甚至多想想也能想出大概的方法:分别设两个指针cut1,cut2,将第一个数组切割成 left1和right1,将第二个数组切割成left2和right2,用二分查找 找到left1和left2中的数都小于等于right1和right2中的数,则中位数在两个cut处产生。(我讲的远远没有leetcode里面各位大佬的题解详细,值得去一看)。
但是,这其中的很多边界,细节等,便是真正的难点所在。
m+n为奇数怎么办,为偶数怎么办,cut越界怎么办······
考虑到各个方面,正真要写出代码还是很困难的。
于是我想出了目前对我来说最容易理解的思路:
若m+n为偶数,不谈,就希望他是偶数,因为这样的话中位数就=(左边最大数+右边最小数)/2.0。
若m+n为奇数,这就很令人头秃。这里我提供一个比较巧妙的思路:
例如两个数组nums1=[1,3,5] nums2=[2,4]。
寻找这两个数组中的中位数 其实就相当于寻找num1'=[1,1,3,3,5,5]和nuns2'=[2,2,4,4]两个数组的中位数
此刻数组长度总数变成了偶数,而变化后的数组中任意一个数字的下标/2等于原数组中这个数字的下标。
那么这个数组*2的变化我们并不需要实际实现,只是看成“虚拟数组”,利用这个虚拟数组更方便地控制原数组的下标关系。
而这个虚拟数组的操作对于m+n为偶数也适用。
奇妙吧,这样下来,就可以把m+n的奇偶情况统一起来了。
下面是代码:
class Solution {
public:
double findMedianSortedArrays(vector<int>& nums1, vector<int>& nums2) {
int m =nums1.size(),n=nums2.size();
if(m>n)
return findMedianSortedArrays(nums2,nums1);// 必须 让nums1的长度小于nums1否则的话m很大n很小,m二分的话会使得Nums2越界
int c1,c2;
int lo =-1,hi = 2*m; //我们这里的c1 c2表示切割的左半部分的最后一个数字的下标 所以c1的范围为[-1,2*m]
int lmax1 ,lmax2,rmin1,rmin2;
while(lo<hi)
//-1 6 c1=2 c2=0
{ //-1 2 c1=0,c2=2
c1=floor((lo+hi)/2.0); //因为二分范围的左边界是-1 为了使得-1/2结果为-1 所以要用floor函数
c2=m+n-2-c1; //因为(c1+1)+(c2+1)=总数的一半=(2*m+2*n)/2
lmax1 =c1<0?INT_MIN:nums1[c1/2]; //如果c1为-1的话,则nums1的切割全部属于右半边
lmax2 =c2<0?INT_MIN:nums2[c2/2];//同上
rmin1= c1>=2*m-1?INT_MAX:nums1[(c1+1)/2];//如果c1为2*m-1即最右边的话,nums1的切割全部属于左半边
rmin2= c2>=2*n-1?INT_MAX:nums2[(c2+1)/2];//同理
if(lmax1>rmin2)
hi=c1;
else if (lmax2>rmin1)
lo=c1+1;
else
break;
}
return (min(rmin1,rmin2)+max(lmax1,lmax2))/2.0;
}
};
那么我这道题苦想了三天的意义是什么?学到了什么新知识?获得了什么新技能?
都没有。
那还有什么意义呢?
有。
再遇难题,我必从容自若。


