题目啊常规解法(DFS)在此就不赘述了。。。
直接进入正题。
众所周知,N皇后是NP完全类问题,n稍微大了点求解过程就会变得很长。
算法方面很难再有质的效率突破,但这不妨在其他细节上下下功夫。
揆诸常规解法,采用了数组来做mark,以行为每一层进行回溯算法,每个操作周期中无非就做了下面这些事情:
更新元素
判定元素
做出反应
更新元素这上面基本上想不到能有啥提升空间了(一次更新多个??似乎更加复杂了不谈不谈)。。。
做出反应嘛也同样没啥可以进步的地方(做出预判类反应??也复杂了,不谈不谈)。。。
很显然,有提升空间的就是判定元素环节了。
首先,从存储上考虑:
我们采用了三个数组来分别mark两个斜线和一列的占用情况(这里用"占用情况"表示此处是否能落子,如果被‘占用了’,则不能放棋子)
可不可以并成一个数组呢?那么这一个数组就要能够表示三个信息:当前位置一列两斜线的占用情况。有时即使能表示了,但是当移动到下一个位置的时候又得获得新的信息。。似乎不可行。
(于是我们又开始无聊地在纸上模拟算法过程了。。。。)
诶,然后就会发现,当进行DFS的时候,比如进行到第k层,放下了一个棋子,然后我们就要到下面一层去继续判定,此刻我们用到的信息是第k+1层的占用情况,而k+1的占用情况受到第k层情况的直接影响,如下图:
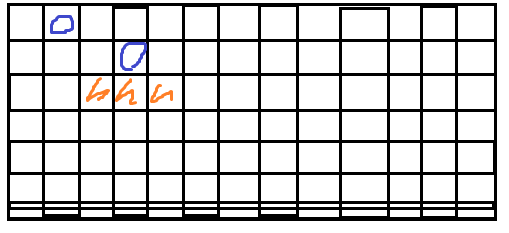
我们会发现第三层涂色的三个位置就不能放棋子了,
而除了第k层的影响,前k-1层也对第k+1层有着制约:
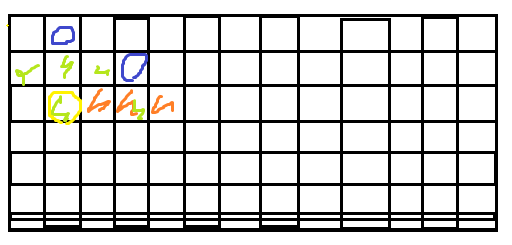
再回来看经典算法,每一次标记直接就否定了一条线上的位置,我们跳出这个思维,可不可以“步步为营”,进入到下一行的同时更新出下一行的占用信息?如果这样的话,一个数组足矣。
再思考,都已经一个数组了(相当于一串数字),而且每个格子就两个状态:有棋子,没棋子。
显然,二进制是不二选择!而且二进制运算的效率比较高!
大概的思路出来了,还有最后一个难点,就是前k-1层的占用信息如何安全过度到第k+1行。。
动手尝试了就不难发现这个规律:一个棋子会产生三种影响效果,斜向影响的,到下一层“占用”会斜向相应的方向偏移一格;垂直影响的,到下一层“占用”依旧在相应位置。
如图:

这时候就出现了三种类型的信息更新,一串二进制就难以实现了。。。那就三串呗,比起数组仍然不亏了。
大的逻辑疙瘩在脑子里基本上解开了,下面开始改代码:
首先,咱不用数组,改成int就够了。其次,考虑到每次信息更新的特点,我们可以用函数的形参来传递,省的搞个全局变量让人不爽。
函数头这亚子:
void Dfs(int i,int left,int col,int right)//分别是 层数 反斜杠mark 一列mark 斜杠mark
然后仍然是一般DFS解法的框架,只需要把其中用bool数组mark判断的地方用二进制方法进行替换即可。
放代码:
1 void Dfs(int i,int left,int col,int right)//分别是 层数 反斜杠mark 一列mark 斜杠mark 2 { 3 if (i > N) //判断是否已经枚举完了N行 4 { 5 showOneSolution(); //枚举完了就输出(此刻我们处于N+1行) 6 return; //返回到第N行 7 } 8 for (int j = N-1; j >=0; --j) //为啥J倒过来数呢?方便下面if中的偏移判断 9 { 10 if (!(((left|col|right)>>j)&1))//(自己解读,有助于提升能力 (好吧我懒)) 11 { 12 ans[i] = N-j; 13 Dfs(i + 1,(left|(1<<j))<<1,(col|(1<<j)),(right|(1<<j))>>1); //更新“占用信息”的工作就放在参数传递这里了 14 //这样子的好处就是,回溯的时候不用做什么恢复处理, 15 //因为这一层的东西基本没变动 16 } 17 } 18 }
这么多括号嵌套的。。哎呀我知道这可读性差,不提倡不提倡!
但是咱们现在是学习又不是工作,尽量读一些奇怪的代码有助于提高读代码能力(可着劲找借口··)
好了下面放上完整代码:
1 #include<iostream> 2 3 using namespace std; 4 5 int total = 0; 6 int N = 0; 7 int ans[64] = { 0 }; //结果还是要用数组存滴 8 void showOneSolution()//用来显示一个解 9 { 10 total++; 11 for (int i = 1; i<=N; ++i) 12 { 13 cout << ans[i] << " "; 14 } 15 cout << endl; 16 } 17 void Dfs(int i,int left,int col,int right)//分别是 层数 反斜杠mark 一列mark 斜杠mark 18 { 19 if (i > N) //判断是否已经枚举完了N行 20 { 21 showOneSolution(); //枚举完了就输出(此刻我们处于N+1行) 22 return; //返回到第N行 23 } 24 for (int j = N-1; j >=0; --j) //为啥J倒过来数呢?方便下面if中的偏移判断 25 { 26 if (!(((left|col|right)>>j)&1))//(自己解读,有助于提升能力 ) 27 { 28 ans[i] = N-j; 29 Dfs(i + 1,(left|(1<<j))<<1,(col|(1<<j)),(right|(1<<j))>>1); //更新“占用信息”的工作就放在参数传递这里了 30 //这样子的好处就是,回溯的时候不用做什么恢复处理, 31 //因为这一层的东西基本没变动 32 } 33 } 34 } 35 36 int main() 37 { 38 cin >> N; 39 Dfs(1,0,0,0); 40 cout << total; 41 system("pause"); 42 return 0; 43 }
总结:
巧妙运用位运算可以达到锦上添花的效果(装逼),不过大多数人看到位运算&|^<<>>啥的就打哈欠。
但是恰巧就有那么一些问题,能够完美契合二进制和位运算的特殊性质(不是指这个==),当你遇到的时候,你就会惊异于0101010···的奇妙。
后记:
当年还是太年轻,其实既然都用了位运算,为何不用用这个绝妙的性质呢?
x & (−x) 可以获得 x 的二进制表示中的最低位的 1 的位置;
x & (x−1) 可以将 x 的二进制表示中的最低位的 1 置成 0。



