ACM-ICPC 2018 南京赛区网络预赛 B The writing on the wall(思维)

https://nanti.jisuanke.com/t/30991

题意

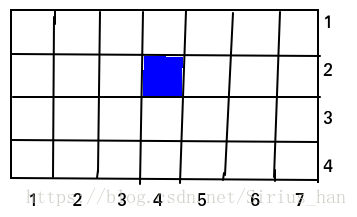
一个n*m的方格矩阵,有的格子被涂成了黑色,问该矩阵中有多少个子矩阵,子矩阵不包含黑色格子。

分析

参考https://blog.csdn.net/Sirius_han/article/details/82313029

n=1e5，m=100。首先思考一下没有黑点的话，子矩阵总数怎么算。

现有长为L的大矩阵，对于固定高度h，其子矩阵的个数是这样计算的

for(int i=1; i<=L; i++){
    for(int j=i; j>0; j--){
        count+=h;
    }
}

那么对于不同高度，只需要再加一维循环就好。

解决有黑点的问题，当存在黑点时

先看高为H(4)的子矩阵个数：以(4, 7)为右下角的高为H的子矩阵个数为3个，由L=4处再向左，就只能构成高为2的子矩阵了；

那么怎么该上边的代码才能得出答案呢？如下：

for(int i=1; i<=H; i++){
    for(int j=1; j<=L; j++){
        h=i;
        for(int k=j; k>0; k--){
            h=min(h, i-p[k]);
            count+=h;
        }
    }
}
//p[k]表示第k列中在i行上边的第一个黑点的位置，

那么维护p数组就是这题的重点了

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
int b[100010][110], up[110];
int main(){
    int T, cas=0;
    scanf("%d", &T);
    while(T--){
        int n, m, K;
        scanf("%d%d%d", &n, &m, &K);
        for(int i=0; i<=n; i++){
            for(int j=0; j<=m; j++){
                b[i][j]=0;
                up[j]=0;
            }
        }
        for(int i=0; i<K; i++){
            int x, y;
            scanf("%d%d", &x, &y);
            b[x][y]=1;
        }
        ll ans=0;
        for(int i=1; i<=n; i++){
            for(int j=1; j<=m; j++){
                if(b[i][j]){
                    up[j]=i;
                }
            }
            for(int j=1; j<=m; j++){
                ll minn=0x7f7f7f7f7f7f7f7f;
                for(int k=j; k>0; k--){
                    minn=min(minn, (ll)(i-up[k]));
                    ans+=minn;
                }
            }
        }
        printf("Case #%d: %lld\n", ++cas, ans);
    }
    return 0;
}

 

 

 

1. #include <bits/stdc++.h>
2.  
   using namespace std;
3.  
   typedef long long ll;
4.  
   int b[100010][110], up[110];
5.  
   int main(){
6.  
   int T, cas=0;
7.  
   scanf("%d", &T);
8.  
   while(T--){
9.  
   int n, m, K;
10.  
    scanf("%d%d%d", &n, &m, &K);
11.  
    for(int i=0; i<=n; i++){
12.  
    for(int j=0; j<=m; j++){
13.  
    b[i][j]=0;
14.  
    up[j]=0;
15.  
    }
16.  
    }
17.  
    for(int i=0; i<K; i++){
18.  
    int x, y;
19.  
    scanf("%d%d", &x, &y);
20.  
    b[x][y]=1;
21.  
    }
22.  
    ll ans=0;
23.  
    for(int i=1; i<=n; i++){
24.  
    for(int j=1; j<=m; j++){
25.  
    if(b[i][j]){
26.  
    up[j]=i;
27.  
    }
28.  
    }
29.  
    for(int j=1; j<=m; j++){
30.  
    ll minn=0x7f7f7f7f7f7f7f7f;
31.  
    for(int k=j; k>0; k--){
32.  
    minn=min(minn, (ll)(i-up[k]));
33.  
    ans+=minn;
34.  
    }
35.  
    }
36.  
    }
37.  
    printf("Case #%d: %lld\n", ++cas, ans);
38.  
    }
39.  
    return 0;
40.  
    }