1.神经网络的起源
在传统的编程方法中,我们通常会告诉计算机该做什么,并且将一个大问题分解为许多小的、精确的、计算机可以轻松执行的任务。相反,在神经网络中,我们不告诉计算机如何解决问题,而是让计算机从观测数据中学习,自己找出解决方法。
自动从数据中学习听起来不错,然而,2006年之前我们都仍然不清楚如何训练神经网络使其优于大多数传统方法,除了一些有专门解决方法的问题。在2006年,深度神经网络出现了,这些技术现在被称为深度学习,它们已经取得了进一步的发展。如今,深度神经网络和深度学习在计算机视觉、语音识别及自然语言处理等重要领域都有卓越的性能表现,并且被谷歌、微软和Facebook等公司大规模应用。
2.神经网络的应用实例——识别手写数字
考虑下列手写数字。大多数人都能轻易地识别这些数字分别是:504192.
![]()
听起来似乎很轻松,但实际上并不是这样的。在我们人脑的两个半球,有一个初级视觉皮层,也就是V1,包含了1.4亿个神经元,它们之间的连接更是多达上百亿个。然而,人类视觉系统不只是V1,而是包含了一整个系列的视觉皮层——V2,V3,V4,V5——以逐渐复杂地对图像进行处理。
人类的大脑就像一台超级计算机,经过上亿年的进化,从而更好地了解视觉世界。实际上,识别手写数字并不容易,更准确地说,人类总是惊人地理解我们的眼睛所呈现给我们的信息。但几乎所有工作都是无意识的,所以我们常常不清楚我们的视觉系统完成了多么困难的任务。
想要编写程序来识别这些手写数字是十分困难的,最直观的经验是“上边有一个环路、右边有一竖就是一个9了”,显然用算法很难表达。当你想要得到这样精确的规则描述时,你会很快迷失在特例和警告等特殊情况的困境中。这样看起来似乎没什么希望了。
而神经网络却能以一种不同的方式来解决这个问题。它的思想是:将大量手写数字作为训练实例,通过学习这些实例而获得一个系统,这个系统就可以用来识别其它的手写数字了。换句话说,神经网络能利用这些实例自动地推断出规则,从而识别手写数字。如果增加训练实例的数量,网络可以学到更多的知识,从而提高识别的准确率。目前最好的商业神经网络(识别手写数字)用于银行处理支票以及邮局识别信封上的地址。实现手写数字识别的设计细节及代码见此。

接下来介绍关于神经网络的许多关键思想,包括两种重要类型的人工神经元——感知器和sigmoid神经元,以及神经网络的标准算法——随机梯度下降法。
3.感知器
感知器在1957年由科学家Frank Rosenblatt提出,它可以被视为一种最简单形式的前馈神经网络,是一种二元线性分类器。
3.1 感知器是如何工作的
一个感知器需要多个二进制输入x1,x2,……,并生成一个二进制输出。下图中的感知器有三个输入x1,x2,x3,Rosenblatt提出一个简单的规则来计算输出。
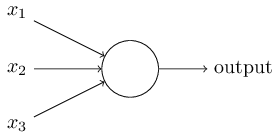
他引入了权值w1,w2,……,这些权值都是实数,分别表示各个输入对输出的重要性。感知器的输出为0或1,取决于输入的加权和∑wixi是否大于一个阈值。和权值一样,阈值也是实数,是神经元的一个参数。用公式表示输出如下图:

这是一个基本的数学模型。你可以将感知器想象为一种设备,这个设备通过权衡各种证据(即输入)做出决定(即输出)。显然,感知器不是人类决策系统的一个完整的模型,但一个复杂的感知器可以做出非常的决定:
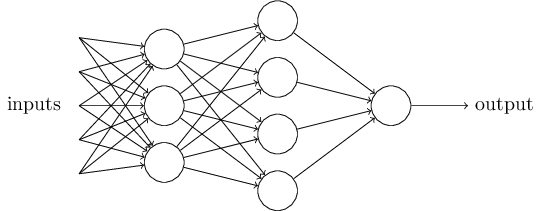
在这个网络中,感知器的第一层通过权衡输入而做出三个非常简单的决定,第二层通过权衡第一层的输出而做出四个稍微复杂的决定,第三层通过权衡第二层的输出做出更复杂的决定,也就是感知器最终的输出。这样的话,多层感知器就可以做出复杂的决策。
为了简化公式(1),我们使用w表示wi组成的向量,即权值向量;x表示xi组成的向量,即输入向量;并将阈值移到不等式的左边,然后用感知器的偏差b来代替阈值,感知器的公式就可以表示为:

可见,如果感知器的偏差b是一个很大的正值,该感知器很容易输出1,相反,如果b是一个很大的负值,该感知器很难输出1。引入偏差b这个概念变化看似很小,实际上使得公式得到了极大的简化。我们不再需要阈值这个概念,而是偏差b。
3.2 感知器的应用
上面我们提到感知器可以权衡各项输入做出决策,而它的另外一个应用就是做最基本的逻辑运算,也就是与、或、与非。举个例子,假如我们有一个感知器,它需要两个输入,每个输入的权值都是-2,偏差是3,如下图左。当我们输入00时,0*(-2)+0*(-2)+3=3,为正数,所以输出为1;同样的,输入为01和10时,输出都为1。而当输入为11时,计算结果为-1,为负数,所以输出为0。也就是说,当输入为00、01、10时,输出为1;输入为11时,输出为0。那么,这个感知器就实现了与非的功能。
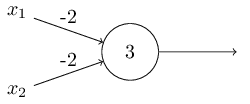
实际上,感知器可以实现任意逻辑运算。是因为与非是最基本的运算,我们可以在与非的基础上实现其它逻辑运算,如上图右。更多逻辑运算的例子见此。
就像与非是逻辑运算中的通用计算一样(universal for computation),感知器也是神经网络中的通用计算。感知器的计算通用性既让人宽心又让人沮丧:让人宽心是因为它告诉我们,感知器网络可以像任何其他计算设备一样强大;让人沮丧是因为它看起来就好像仅仅只是与非门的一种新类型。
但实际上的情况比这要好点。事实证明,我们可以设计学习算法来自动调整人工神经元网络的权值和偏差。这个调整过程是对外部刺激的直接反应,而不需要程序员去干预,这一点是与传统的逻辑门不同的。也就是说,我们的神经网络是可以简单地自己学会去解决问题的,这些问题不是直接设计一个传统的逻辑回路能解决的。
4.sigmoid神经元
4.1 感知器的局限
学习算法,听起来不错。但是我们如何为一个神经网络设计这样的算法呢?假设现在我们有一个感知器网络,我们想要让其学会解决问题。举个例子,网络的输入可能是一个手写数字的扫描图像的原始像素数据。现在我们希望这个网络能学习到合适的权值和偏差,使得网络的最终输出能正确将这个数字分类。
为了看看这个学习过程是如何进行的,我们对网络中一些权值(或偏差)做小小的改动。我们想要看到的是,对于权值的小小改动,将会导致网络输出有相应的改变。(我们稍后将会明白,这样的属性是使得学习过程成为可能的关键)大致意思如下图所示:(当然,对于手写数字识别的问题,下面这个网络太简单了)
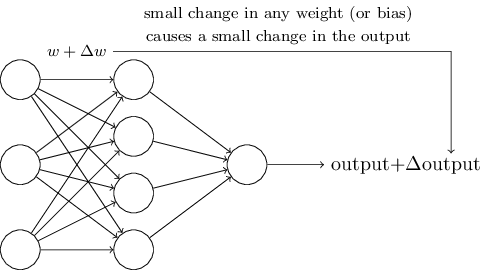
如果前面我们假设的“权值(或偏差)的改变能引起输出的改变”是事实,那么我们就可以利用这一点去修改权值和偏差,使得我们的网络按照我们的意愿去工作。比如说,我们的网络将“9”识别成了“8”,我们就可以想办法改变权值和偏差,使得网络更大可能地将图像识别成“9”。然后我们就可以重复这一过程,不断地改变权值和偏差,使得输出越来越接近理想值。这样看来,我们的网络就具备了学习的能力。
问题是,当我们的网络包含感知器时,并不会发生这样的过程。事实上,在任何一个感知器中,对权值或偏差的小小改动可能会导致该感知器的输出完全翻转,也就是说从0变为了1。而这样的翻转可能会导致感知器接下来的识别工作发生彻底改变。所以说,就算你的“9”被识别正确了,对其它数字的识别可能会以难以控制的方式发生改变,比如将“6”识别成了“8”。
4.2 sigmoid神经元的出现
显然,想要感知器具备学习能力是困难的。也许有更好的办法,但这样的可能似乎并不明显。现如今,使用的是另一种更常见的人工神经元模型——sigmoid神经元,它可以克服这个问题。sigmoid神经元和感知器类似,但是它可以通过修改权值和偏差,使得输出发生相应的变化。这使得sigmoid神经元网络具备学习能力。
就像感知器一样,sigmoid神经元也有输入x1,x2,……,但不像感知器的输入只能是0或1,sigmoid神经元的输入可以是0到1之间的任意值,比如0.638。它也有权值w1,w2,……,以及整体偏差b。它的输出也不再是0或1,而是σ(w*x+b),其中σ是sigmoid函数(sigmoid function),且其定义式如下右图:


更明确地,一个sigmoid神经元的输出如下图式子所示。乍一看,sigmoid神经元好像与感知器完全不同。事实上,它们俩有许多相似之处。

为了更好地理解其中的相似之处,我们假设 z=w*x+b 是一个大的正数,所以 e^(-z)≈0,σ(z)≈1。也就是说,当 z=w*x+b 是一个很大的正数时,sigmoid神经元的输出就很接近1,就像在感知器中一样。相反,当 z=w*x+b 是一个绝对值很大的负数时,sigmoid神经元的输出就很接近0,也类似于感知器。只有当 z=w*x+b 处于中间值时,sigmoid才与感知器不同。
4.3 sigmoid函数的形式
事实上,σ的确切形式并不重要,真正重要的是函数的形状。上述提到的σ函数的形状如下图左。如下图右是一个平滑的阶跃函数。如果σ真的是一个阶跃函数,那么sigmoid神经元就变成了一个感知器,因为输出0或1就完全取决于 w*x+b 的正负了(实际上,当 w*x+b=0 时,感知器的输出为0,而阶跃函数的输出为1。所以,严格来讲,要想完全等于感知器,我们必须调整阶跃函数在0点的值)。


可以发现,是σ函数的平滑度起了关键作用,而不是其具体形式。σ的平滑度意味着权值的变动Δwj或偏差的变动Δb将会对神经元的输出所做的改变Δoutput,微积分可以给出Δoutput的近似值。下面这个公式告诉我们:Δoutput是Δwj和Δb的线性函数。所以sigmoid神经元能更容易地指出权值和偏差的改变是如何改变输出的。

既然是σ函数的平滑度起了关键作用,而不是其具体形式,那么为什么用公式(3)中的形式呢?事实证明,当我们计算这些偏导数时,使用σ将简化代数,仅仅因为指数很容易求微分。在任何情况下,σ在神经网络中是被广泛使用的,常作为激活函数。
4.4 sigmoid神经元的输出
显而易见,sigmoid神经元与感知器最大的不同就是输出不再仅仅只是0或1,它可以输出0-1之间的任意实数。这个属性很有用,例如,如果我们想用输出值表示一个输入图像中像素的平均强度。
但有时它又显得很麻烦,假如我们想用网络的输出来表示“输入图像是9”和“输入图像不是9”中的一个。显然,此时用感知器会更简单。不过在实际应用中,我们可以设置一个规则来解决这个问题。例如,规定输出大于或等于0.5时表示“输入图像是9”,输出小于0.5时表示“输入图像不是9”(对图片的像素强度进行编码,如64*64个像素单元,就是64*64个输入,输出是一个介于0到1之间的值,最后比较其与0.5的大小)。
5.其它人工神经元模型
原则上,由sigmoid神经元组成的网络可以计算任何函数。然而实际中,使用其它神经元模型组成的网络有时性能会胜过sigmoid神经元的网络,可能学习地更快,可能对测试数据更泛化,也可能两者都有。下面我们就列举几个其它神经元模型。
5.1 tanh神经元
最简单的变种——tanh神经元,用双曲正切函数替代sigmoid函数。一个“输入为x,权值向量为w,偏差为b”的tanh神经元的输出如下图所示。
tanh(x)=2f(2x)-1 。
它非常接近sigmoid神经元。我们知道tanh函数的公式如下式(110),可以推导出它和sigmoid函数的关系如式(111)所示。所以说,tanh函数相当于只是sigmoid函数的变种,并且可以在曲线图中看出tanh函数和sigmoid函数有相同的形状。
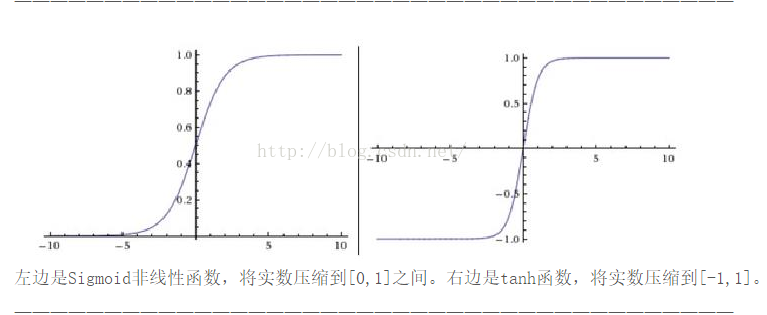
唯一的不同是:tanh神经元的输出范围为[-1,1],而sigmoid神经元的输出为[0,1]。也就意味着,如果你在网络中使用tanh神经元,你必须对你的结果进行归一化(根据实际,也可能需要对输入归一化)。
和sigmoid神经元类似,tanh神经元也可以计算任何函数(compute any function),将输入mapping到[-1,1]。此外,像BP和随机梯度下降法也可以很容易地应用于tanh神经元的网络中。
5.2 ReLu(自适应线性神经元)
sigmoid神经元的另一个变种就是自适应线性神经元ReLu(rectified linear neuron or rectified linear unit),一个“输入为x,权值向量为w,偏差为b”的ReLu的输出如下式(112)。用图来表示自适应函数 max(0,z) 如下所示。
很明显,这样的神经元是与tanh神经元和sigmoid神经元都非常不同的。不过,ReLu神经元也是可以计算任何函数的,也可以用BP和随机梯度下降法等思想来训练。
那么,我们什么时候用ReLu而不是tanh神经元或sigmoid神经元呢?目前已经有许多在图像识别上的工作发现了相当多使用ReLu的好处。
6.神经网络的结构
神经网络的结构如下图,中间的隐藏层可以有多个。令人困惑的一点是,由于历史原因,这样的多层网络有时又被称为多层感知器或MLPs(multilayer perceptrons),尽管这些神经元是由sigmoid神经元组成的,而不是感知器。
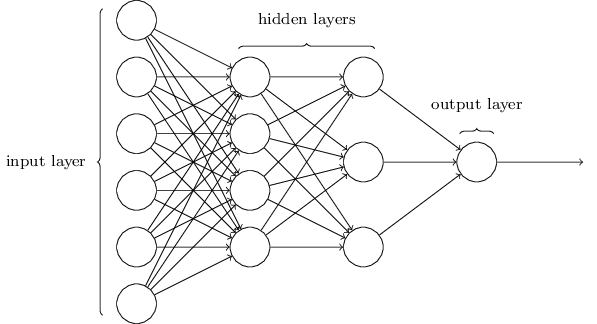
输入层和输出层的设计是显而易见的,而隐藏层的设计则是一门艺术活,我们无法用几个简单的经验法则就总结出隐藏层的设计过程。相反,神经网络的研究人员们已经开发了许多设计隐藏层的启发式方法,使得人们能得到他们满意的网络。这样的启发式方法能权衡隐藏层的数目和训练网络需要的时间两者之间的力臂。
一层的输出作为下一层的输入,这样的网络称为前馈神经网络。这意味着网络中不存在回环,信息总是向前传播,并不会反馈。如果网络中存在回环,我们将会陷入死循环:σ函数的输入取决于输出。这将会很难理解,所以我们不允许这样的回环存在。
然而,还有其他允许反馈循环的人工神经网络模型,这些神经网络被称为递归神经网络。这些模型的思想是:存在一些只在有限时间内产生作用的神经元。这样的神经元可以刺激其他神经元,其他神经元可能会在一段时间后产生作用,但也只能持续一段时间。接着再激活其他神经元,所以随着时间推移,我们会得到神经元激活的一个级联。在这样的模型中,回环不会产生什么问题,因为一个神经元的输出只会在一段时间后才对其自身的输入产生作用,并不是瞬时的。
递归神经网络(RNN)的影响不如前馈神经网络,部分原因是RNN的学习算法并不是很强大(至少迄今为止是这样)。但RNN仍然非常有趣,它们更接近人类大脑的运作方式。并且RNN很有可能能解决用前馈网络很难解决的问题。
7.神经网络向深度学习的发展
假如我们想确定一张图像中是否有人脸,处理这个问题和识别手写数字是一样的方式。图像中的像素作为神经网络的输入,网络的输出是单个神经元,并指示“Yes, it’s a face”或“No, it’s not a face”。
如果我们手动设计一个网络会怎么样?我们必须选择合适的权值和偏差。这个时候,让我们完全忘记神经网络的概念,我们所能想到的启发式方法就是我们可以将这个问题分解成子问题:图像中是否有左眼?图像中是否有右眼?图像的中间是否有鼻子?图像的中下部是否有嘴巴?图像的顶部是否有头发?等等问题。
如果像这类问题的多个都是“yes”,或者说“probably yes”,那我们就可以得出结论:这个图像很有可能是一张人脸。如果像这类问题的多个都是“no”,那我们就可以得出结论:这个图像很有可能不是一张人脸。
当然,这样去判断是很粗糙的,也有很多缺陷:也许这个人是一个秃子呢,所以他没有头发;也许我们看见的只是人脸的一部分,或者人脸不是正向朝向我们的,所以人脸的一部分特征被遮蔽了。
下面有一个也许可行的结构,其中一个矩形表示一个sub-network,也就是上面我们列举的那些子问题。注意,这不是一个现实的方法来解决人脸识别的问题,它只是用来帮助我们直观地感受网络是如何工作的。
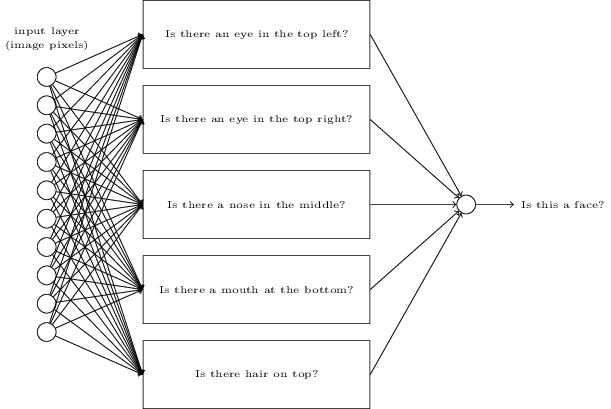
显而易见,这些子问题也是可以再一次被分解的。比如,对于“是否有左眼”的问题,可以进一步分解为:“是否有眉毛”、“是否有睫毛”、“是否有虹膜”等等。当然,这些子子问题还包括位置信息,比如“眉毛是否在虹膜的上方”等,但这里让我们尽可能地简化。所以说,“是否有左眼”的问题可做如下分解:
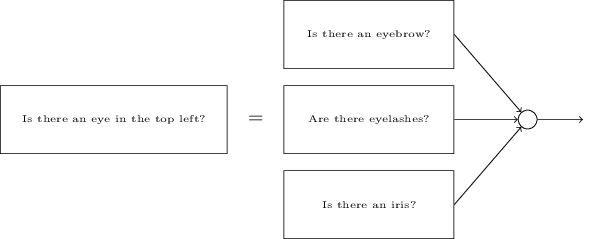
当然,其中的子子问题又可以进一步分解,通过分解多层来更进一步。直到最后,我们可以用像素这一层次来回答问题,比如“图像中特定的位置是否出现简单的形状”这一类的问题。最后,网络就将一个很复杂的问题分解成了非常简单的问题。
这个网络会有很多层,从具体到抽象,从复杂到简单。这样多层结构的网络(具有两层或更多隐藏层)就被称为深度神经网络(deep neural networks)。
我们当然没法人工来选择网络的权值和偏差,我们还是必须使用学习算法使得网络能自动地从训练数据中学习到合适的权值和偏差。1980s和1990s,研究人员们尝试使用随机梯度下降法和反向传播算法来训练深度网络,不幸的是,除了少数特殊结构,并没有什么大的进展。网络可以学习,但是很慢,因此没什么用。
但自2006年以来,一系列的技术被发明,使得深度网络的学习成为可能。虽然这些技术仍是基于随机梯度下降法和反向传播算法,但也有一些新的思想。这些技术使得更深(或更大)的网络得到训练——人们现在普遍训练的网络的隐藏层有5-10层。并且事实证明,在许多问题上,这些技术远比浅层神经网络(隐藏层只有一层的网络)的性能更好。
这其中的原因肯定是深度网络能建立更复杂的层次结构,这就像传统编程语言使用模块化的设计以及抽象的思想从而能创建复杂的计算机程序一样。当然,在神经网络和传统编程中,抽象是不同的形式,但都是同等重要的。
参考文献:
- Michael A.Nielsen, “Neural Networks and Deep Learning“, Determination Press, 2015.
- ReLu的好处:Kevin Jarrett, Koray Kavukcuoglu, Marc’Aurelio Ranzato and Yann LeCun, “What is the Best Multi-Stage Architecture for Object Recognition?” (2009)
- ReLu的好处:Xavier Glorot, Antoine Bordes, and Yoshua Bengio, “Deep Sparse Rectifier Neural Networks” (2011)
- ReLu的好处:Alex Krizhevsky, Ilya Sutskever, and Geoffrey Hinton, “ImageNet Classification with Deep Convolutional Neural Networks” (2012)
- ReLu的好处:Vinod Nair and Geoffrey Hinton, “Rectified Linear Units Improve Restricted Boltzmann Machines” (2010)
- 安逸轩的博客:http://andyjin.applinzi.com/





