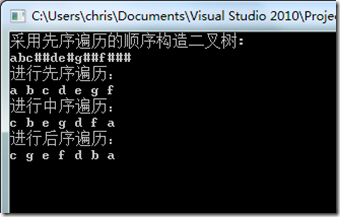
1.构造二叉树:
采用先序遍历的顺序来读入数据,递归构造二叉树。相应代码:
int CreateBiTree(TREE **t)
{
char ch;
scanf("%c",&ch);
if(ch=='#') (*t)=NULL;
else
{
*t=(TREE *)malloc(sizeof(TREE));
if(t==NULL)
return 0;
(*t)->data=ch;
CreateBiTree(&((*t)->lchild));
CreateBiTree(&((*t)->rchild));
}
return 1;
}
在这个函数中传入的TREE**t是指针的指针,由于在一颗书中要创建新的节点放到根节点(TREE *)下,这必然要改变指针的指向,因此用指针的指针,否则这里的t只是一个指针,调用完后就失效了,root这棵树还是一颗空树。这里用‘#’来表示空,每次读入都要判断,若不空就为*t开辟一个内存空间,将值存到该节点,然后再递归构造它的左子树和右子树。在调用时注意参数是&((*t)->lchild),而不是(*t)->lchild)。
2.遍历二叉树(先序、中序、后序):
2.1.先序遍历递归算法:
void PreOrder1(TREE *t)
{
TREE *p=t;
if(t==NULL)
printf("空树!!!");
else
{
printf("%c",t->data);
PreOrder1(t->lchild);
PreOrder1(t->rchild);
}
}
该递归算法很形象地体现了先序遍历的思想,先访问,再遍历左子树,后遍历右子树。可见递归的确非常简洁易于理解。
2.2、先序遍历非递归算法:
void PreOrder2(TREE *t)
{
TREE *st[100],*p;//顺序栈st中保存的是节点指针,而不是节点值
int top=-1;
if(t==NULL)
printf("空树!!!");
else
{
top++;
st[top]=t;//根节点进栈,由于栈中保存的是节点指针,因此不能直接放t->data
while(top>-1)//在栈不空的时候循环遍历该节点和左子树右子树
{
p=st[top];//栈顶元素出栈
top--;
printf("%c ",p->data);//体现了先序遍历,先访问该节点
//此处注意入栈顺序,考虑到栈的特点后进先出,所以你先要遍历的是左子树,左子树后入栈
if(p->rchild!=NULL)//若有右孩子,右孩子入栈
{
top++;
st[top]=p->rchild;
}
if(p->lchild!=NULL)
{
top++;
st[top]=p->lchild;
}
}
printf("\n");
}
}
该算法应用栈来存放数据,由于栈本身的特点就是只对一段进行操作,后进先出,用它来存放节点数据,由先序遍历的过程可知,先访问根节点,再访问左子树后访问右子树。因此先将根节点进栈,在栈不空的时候循环:出栈p,访问*p节点,将其右孩子节点进栈,再将左孩子节点进栈。
2.3、中序遍历递归算法:
//中序遍历的递归算法
//与先序遍历类似,变的只是节点访问的次序
void InOrder1(TREE *t)
{
TREE *p=t;
if(t==NULL)
printf("空树!!!");
else
{
printf("%c",p->data);
InOrder1(t->rchild);
InOrder1(t->lchild);
}
}
中序遍历和先序遍历类似,只是访问的顺序变了一下。
2.4、中序遍历的的非递归算法:
void InOrder2(TREE *t)
{
TREE *st[100],*p;
int top=-1;
if(t==NULL)
printf("空树!!!");
else
{
p=t;//p指向根节点
while(top>-1 || p!=NULL)//当栈不空或者数不空的时候循环
{
while(p!=NULL)//当树不空就一直遍历它的左子树,直到左子树为空停止
{
top++;
st[top]=p;
p=p->lchild;
}
if(top>-1)
{
p=st[top]; //出栈*p节点,它没有右孩子或右孩子已访问
top--;
printf("%c ",p->data);//访问它
p=p->rchild;//访问栈顶节点的右孩子,并将它入栈,若右孩子还有左子树返回到while直到左子树为空
}
}
printf("\n");
}
}
由中序遍历的过程可知,采用一个栈保存需要返回节点的指针。先扫描(并非访问)根节点的所有左节点并将他们一一进栈。然后出栈一个节点*p,显然*p节点没有左孩子节点或者左孩子节点已经访问过(表明该节点的左孩子均已访问过),然后扫描该节点的右孩子,将其进栈,再扫描该右孩子节点的所有左节点一一进栈,如此这样,直到栈空。
2.5、后序遍历的递归算法:
void PostOrder1(TREE *t)
{
if(t==NULL)
printf("空树!!!");
else
{
PostOrder1(t->lchild);
PostOrder1(t->rchild);
printf("%c ",t->data);
}
}
2.6、后续遍历的非递归算法:
void PostOrder2(TREE *t)
{
TREE *st[100],*p=t,*q;
int top=-1;
int flag;
do
{
while(p!=NULL)
{
top++;
st[top]=p;
p=p->lchild;
}
q=NULL;//q指向栈顶节点的前一个已经访问过的节点
flag=1;//设置flag=1表示处理栈顶元素
while( flag==1 && top!=-1)
{
p=st[top];
if(p->rchild==q)//该右孩子不存在,或右孩子已经被访问,就访问该节点
{
printf("%c ",p->data);//访问它
top--;//退栈
q=p;//让q指向刚刚访问过的节点,以便下一次判断
}
else//右孩子没有被访问
{
p=p->rchild;//p指向右孩子
flag=0;//表示要退出这个循环,重新进入上一个循环去判断这个节点的左孩子
}
}
}while(top!=-1);
printf("\n");
}
后续遍历的非递归算法,采用一个栈保存需要返回的节点指针,先扫描根节点的所有左节点并一一进栈,出栈一个*p,即当前节点,然后扫描该节点的右孩子节点并进栈,再扫描该右孩子节点的所有左节点进栈,当一个节点的左、右孩子均访问过后在访问该节点,直到栈为空。
从上述过程可知,栈中保存的是当前节点*p的所有祖先节点,均为访问过。该算法比先序和中序复杂,由于它不像先序那样直接访问根节点不必保存,它必须保存所有节点,在访问坐姿束河右子树时,该节点会被遍历到两次,在寻找他的左子树时遍历到一次,然后退栈,当它的右子树没有被访问过且是存在的,先访问他的右子树,最后再次访问该节点。所以这里需要一个变量来专门记录这种情况,就是这里的flag,首先将一棵树的所有左孩子进栈,q用来保存指向栈顶的前一个已经访问过的节点,flag设为1,表示要处理栈顶元素,再进入循环,读栈顶元素,判断他是否有或是否访问过右子树,若已经访问(这里就用到了q,若刚刚访问的q就是现在这个节点的右孩子,那说明访问过了,没有右孩子的情况也一样,因为q就是NULL),那么就取出栈顶元素并输出。若没有访问过,直接访问指向他的右孩子,将flag设为0,因为此时栈顶元素不处理,将要处理他的右孩子了,要退出这个循环,到外层循环再次去遍历他的左子树,如此重复知道栈空。。。。
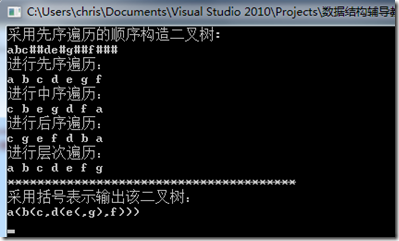
运行结果图:
2.7、层次遍历的非递归算法:
void LevelOrder(TREE *b)
{
TREE *p;
TREE *qu[100];
int front,rear;
front=rear=0;
rear++;
qu[rear]=b;
while(front!=rear)
{
front=(front+1)%100;
p=qu[front];
printf("%c ",p->data);
if(p->lchild!=NULL)
{
rear=(rear+1)%100;
qu[rear]=p->lchild;
}
if(p->rchild!=NULL)
{
rear=(rear+1)%100;
qu[rear]=p->rchild;
}
}
}
首先是定义一个环形队列,用来存放节点指针(NOTE:是节点的指针)第一步将根节点指针入队,队列不空的时候开始循环(就是front!=rear)首先取出队头元素,先访问它,然后判断是否有左孩子,若有就入队,再判断是否有右孩子,有再入队,这个和先序遍历的思想有点类似,但值得注意的是,这里是先将左孩子入队,再右孩子,而先序遍历是先将右孩子入栈再左孩子,这是因为这里用队列存储,先进先出,每次访问对队头元素,这样顺序就是层次遍历的顺序了。
3、括号表示法输出二叉树:
//采用括号表示法输出该二叉树
/*
f(b)==不输出任何内容 当b=NULL
f(b)==输出:b->data(f(b->rchild)) 当左子树不空、右子树为空
f(b)==输出:b->data(,f(b->rchild)) 当左子树空、右子树不空
f(b)==输出:b->data(f(b->lchild),f(b->rchild)) 当左子树不空、右子树不空
f(b)==输出:b->data 当左右子树都为空
*/
void DisBTNode1(TREE *b)
{
if(b!=NULL)
{
if(b->lchild!=NULL && b->rchild==NULL)//左不空右空
{
printf("%c(",b->data);
DisBTNode1(b->lchild);
printf(")");
}
else if(b->lchild==NULL && b->rchild!=NULL)//左空右不空
{
printf("%c(",b->data);
printf(",");
DisBTNode1(b->rchild);
printf(")");
}
else if(b->lchild!=NULL && b->rchild!=NULL)//左右不空
{
printf("%c(",b->data);
DisBTNode1(b->lchild);
printf(",");
DisBTNode1(b->rchild);
printf(")");
}
else
printf("%c",b->data);
}
printf("\n");
}
//进一步优化后的算法
void DisBTNode2(TREE *b)
{
if(b!=NULL)
{
printf("%c",b->data);
if(b->lchild!=NULL || b->rchild!=NULL)
{
printf("(");
DisBTNode2(b->lchild);
if(b->rchild!=NULL)
printf(",");
DisBTNode2(b->rchild);
printf(")");
}
}
}
4、求第k个节点的值:
//假设二叉树采用二叉链存储结构存储,设计一个算法,求先序遍历序列中第k个节点的值
/*
递归模型如下:
f(b,k)='' 当b=NULL时返回特殊字符''
f(b,k)=b->data 当k=n
f(b,k)=((ch=f(b->lchild,k))==''?f(b->rchild,k):ch) 其他情况
*/
int n=1;
char PreNode(TREE *b,int k)
{
char ch;
printf("n=%d ",n);
if(b==NULL)
return ' ';
if(k==n)
return b->data;
n++;
ch=PreNode(b->lchild,k); //递归寻找左子树
if(ch!=' ')//当返回的是一个值而不是' '的时候说明找到了,就返回这个值
return ch;
ch=PreNode(b->rchild,k);//当找遍了左子树后返回的最终还是' '说明没找到,就要往右子树开始找
return ch;
}
该算法是先序遍历的一个应用,首先从根节点开始,判断该节点是否就是要找的节点,若是,直接返回该节点值,若为空,就用特殊符号' '代替(这是为了下次递归遍历的时候用来判断是否找到该节点,因为返回来的值要么就是' ',要么是找到的节点值,就两种情况),若根节点不是要找的节点,就使n递增1,说明要往下一层寻找,先递归他的左子树,在左子树中就找到了该节点,就返回节点值,不再执行下面的操作,若所有的左子树都不是要找的节点,就从最后一层的左节点开始递归他的右子树,直到找到返回为止.
5、求各种节点的个数:
5.1、计算一颗给定二叉树的所有叶子节点的个数:
/*
f(b)=0 若b=NULL
f(b)=1 若*b为叶子节点
f(b)=f(b->lchild)+f(b->rchild) 其他情况
*/
int LeafNodes(TREE *b)
{
if(b==NULL)
return 0;
if(b->lchild==NULL &&b->rchild==NULL)
return 1;
return LeafNodes(b->lchild)+LeafNodes(b->rchild);
}
5.2、计算一颗给定二叉树的所有单分支节点个数:
/*
f(b)=0 若b=NULL
f(b)=f(b->lchild)+f(b->rchild)+1 若*b为单分支
f(b)=f(b->lchild)+f(b->rchild) 其他情况
*/
int SSonNode(TREE *b)
{
if(b==NULL)
return 0;
if((b->lchild==NULL && b->rchild!=NULL) || (b->lchild!=NULL && b->rchild==NULL))
return 1+SSonNode(b->lchild)+SSonNode(b->rchild);
return SSonNode(b->lchild)+SSonNode(b->rchild);
}5.3、计算一颗二叉树的所有双分支节点个数:
/*
f(b)=0 若b=NULL
f(b)=f(b->lchild)+f(b->rchild)+1 若*b为双分支
f(b)=f(b->lchild)+f(b->rchild) 其他情况
*/
int DSonNode(TREE *b)
{
if(b==NULL)
return 0;
if(b->lchild!=NULL && b->rchild!=NULL)
return 1+DSonNode(b->lchild)+DSonNode(b->rchild);
return DSonNode(b->lchild)+DSonNode(b->rchild);
}5.4、计算一颗二叉树的所有分支节点个数:
/*
f(b)=0 若b=NULL
f(b)=f(b->lchild)+f(b->rchild)+1 若*b为分支
f(b)=f(b->lchild)+f(b->rchild) 其他情况
*/
int FSonNode(TREE *b)
{
if(b==NULL)
return 0;
if(b->lchild!=NULL || b->rchild!=NULL)
return 1+FSonNode(b->lchild)+FSonNode(b->rchild);
return FSonNode(b->lchild)+FSonNode(b->rchild);
}
5.5、计算一颗二叉树的所有节点个数:
/*
f(b)=0 若b=NULL
f(b)=f(b->lchild)+f(b->rchild) 其他情况
*/
int TSonNode(TREE *b)
{
if(b==NULL)
return 0;
return TSonNode(b->lchild)+TSonNode(b->rchild)+1;
}
5.6、计算一颗对给定二叉树中值为k的节点个数:
/*
计算一颗二叉树b中值为k的节点个数的递归模型f(b,k)如下;
f(b,k)=0 当b=NULL
f(b,k)=1+f(b->lchild,k)+f(b->rchild,k) 当b->data=k
f(b,k)=f(b->lchild,k)+f(b->rchild,k) 其他情况
*/
int Countk(TREE *b,char k)
{
if(b==NULL)
return 0;
if(b->data==k)
return 1+Countk(b->lchild,k)+Countk(b->rchild,k);
return Countk(b->lchild,k)+Countk(b->rchild,k);
}
6、判断一颗二叉树是否为满二叉树:
/*
由满二叉树的定义可知,若一颗二叉树满足n=2^h-1,则为满二叉树
*/
int height(TREE *b)
{
int lchilddep=0,rchilddep=0;
if(b==NULL)
return 0;
lchilddep=1+height(b->lchild);//递归左子树
rchilddep=1+height(b->rchild);//递归右子树
return lchilddep>rchilddep?lchilddep:rchilddep;//取左右子树深度大的就是树的高度
}
7、复制二叉树:
//假设二叉树采用二叉链表存储结构,设计一个算法把二叉树b复制到二叉树t中。
/*
递归模型如下:
f(b,t)==t==NULL 若b为NULL
f(b,t)==复制根节点*b产生*t节点 其他情况
f(b->lchild,t->lchild);
f(b->rchild,t->rchild);
*/
int Copy(TREE *b,TREE **t)
{
if(b==NULL)
{
t=NULL;
return 0;
}
else
{
*t=(TREE *)malloc(sizeof(TREE));
*t=b;
Copy(b->lchild,&(*t)->lchild);
Copy(b->rchild,&(*t)->rchild);
}
return 1;
}这里TREE **t就是上面介绍过的指针的指针,要改变指针的指向而用,这算法个是基于先序遍历的,首先复制根节点,再左子树、右子树。
8、交换二叉树的左右子树:
//假设二叉树采用二叉链存储结构,设计一个算法把二叉树b的左右子树进行交换,要求不破坏原二叉树
/*
本题要求不破坏原有二叉树,实际上是建立一颗新的二叉树t,它交换了二叉树b的左右子树。递归模型:
f(b,t)==t==NULL 若b为NULL
f(b,t)==复制根节点*b产生*t节点 其他情况
f(b->lchild,t->rchild);
f(b->rchild,t->lchild);
*/
//基于先序遍历
int swap(TREE *b,TREE **q)
{
if(b==NULL)
{
*q=NULL;
return 0;
}
else
{
(*q)=(TREE *)malloc(sizeof(TREE));
(*q)->data=b->data;
swap(b->lchild,&((*q)->rchild));
swap(b->rchild,&((*q)->lchild));
}
return 1;
}
/*如果本题没有要求不破坏原二叉树的条件,或者要求空间复杂数O(1)。这样就不需要另外建立二叉树t,
只需将原叉数的左右子树交换即可,递归模型:
f(b,t) 不做任何事 若b为NULL
f(b,t)== f(b->lchild) 其他情况
f(b->rchild)
将*b节点的左右子树交换
*/
//基于后序遍历
void swap1(TREE **b)
{
TREE *q;
if(*b!=NULL)
{
swap1(&((*b)->lchild));//递归交换b的左子树
swap1(&((*b)->rchild));//递归交换b的右子树
q=(*b)->lchild; //交换b所指的节点的左右指针
(*b)->lchild=(*b)->rchild;
(*b)->rchild=q;
}
}
9、判断二叉树是否相似:
/*假设二叉链采用二叉链存储结构,设计判断两颗二叉树是否相似的算法,所谓二叉树t1和t2相似是指t1和t2都是空二叉树或者t1和t2的根节点是相似的,且t1的左子树和t2的左子树相似,t1的右子树和t2的右子树也相似*/
/*
f(t1,t2)==true 若t1,t2均为NULL
f(t1,t2)==false 若t1t2之一为NULL
f(t1,t2)==f(t1->lchild,t2->lchild)
&f(t1->rchild,t2->rchild) 其他情况
*/
int Like(TREE *t1,TREE *t2)
{
int like1,like2;
if(t1==NULL && t2==NULL)
return 1;
if((t1==NULL && t2!=NULL) ||(t1!=NULL && t2==NULL))
return 0;
like1=Like(t1->lchild,t2->lchild);
like2=Like(t1->rchild,t2->rchild);
return like1&like2;
}
10、判断二叉树是否相等:
//假设二叉树采用二叉链存储结构,设计判断两颗二叉树是否相等
/*
f(t1,t2)==true 若t1,t2均为NULL、
f(t1,t2)==false 若t1,t2之一为NULL
f(t1,t2)==t1->data==t2->data
&f(t1->lchild,t2->lchild)
&f(t1->rchild,t2->rchild) 其他情况
*/
int same(TREE *t1,TREE *t2)
{
int same1,same2;
if(t1==NULL && t2==NULL)
return 1;
if((t1==NULL && t2!=NULL) ||(t1!=NULL && t2==NULL))
return 0;
same1=same(t1->lchild,t2->lchild);
same2=same(t1->rchild,t2->rchild);
if(t1->data==t2->data && same1==1 && same2==1)
return 1;
else
return 0;
}