会员
周边
新闻
博问
闪存
众包
赞助商
Chat2DB
所有博客
当前博客
我的博客
我的园子
账号设置
会员中心
简洁模式
...
退出登录
注册
登录
ffex
博客园
首页
新随笔
联系
订阅
管理
2024年1月6日
快速幂(Fast power)
摘要: 简介(Introduction) 快速幂是快速计算底数的 $n $ 次幂 对于 $a^b \quad mod \quad p $ ,当 $a $ 或者 $b $ 非常大时我们无法直接算出来结果 描述(Description) ,就需要进行拆分。 而快速幂算法可以高效地做到这一点,快速幂算法的核心思想
阅读全文
posted @ 2024-01-06 11:49 TheoFan
阅读(117)
评论(0)
推荐(0)
2023年8月4日
C/C++运算符优先级
摘要: 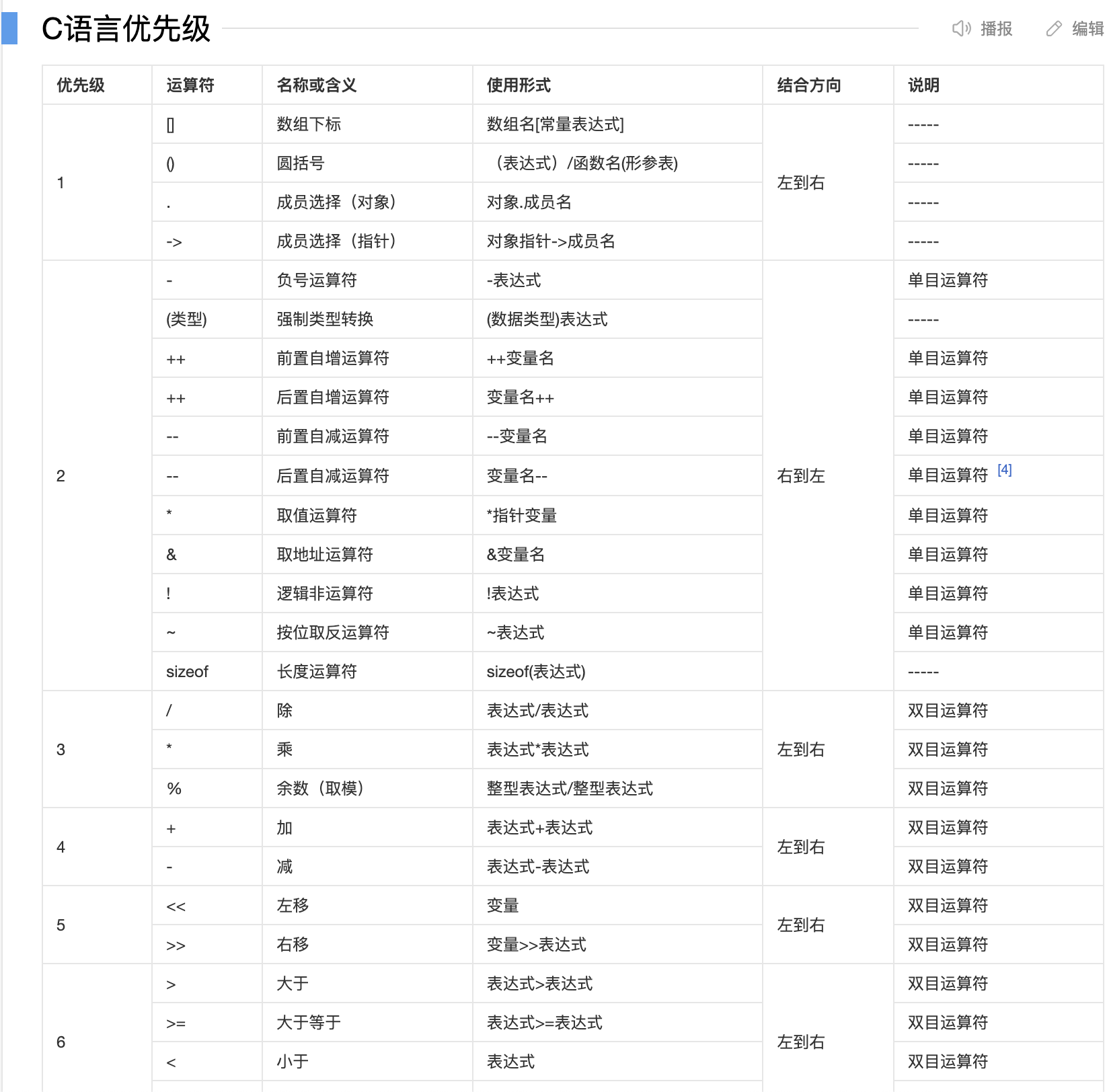 
评论(0)
推荐(0)
2023年8月3日
页式、段式、段页式存储访存次数
摘要: ## 页式/段式 存储:(2次) - 第一次,访问内存中的页表,利用逻辑地址中的页号查找到物理块号,与逻辑地址中的页内偏移拼接形成物理地址; - 第二次:得到物理地址后,再一次访问内存,存取指令或者数据。 ## 段页式 存储:(3次) - 第一次:访问内存中的段表,查到页表的起始地址 - 第二次:访
阅读全文
posted @ 2023-08-03 23:28 TheoFan
阅读(1739)
评论(0)
推荐(0)
2023年6月12日
分治策略(Divide and Conquer)
摘要: ## 简介(Introduction) > 分治策略*(Divide and Conquer)*是对于一个规模为 $n$ 的问题,若该问题可以容易地解决(比如说规模 $n$ 较小)则直接解决,否则将其**分解**为 $k$ 个规**模较小的子问题**,这些子问题互相独立且与原问题形式相同,**递归*
阅读全文
posted @ 2023-06-12 11:20 TheoFan
阅读(127)
评论(0)
推荐(0)
区间合并(Merge-Interval)
摘要: ### 简介(Introduction) > 区间合并就是将坐标轴中两个存在交集的区间合并成一个区间,是一种比较"狭窄"的算法 ## 描述(Description) 1. 将所有区间按照左端点从小到大进行排序 2. 排完序后,当前区间和下一个区间的关系有三种: 1. 下一个区间左右端点在当前区间内
阅读全文
posted @ 2023-06-12 11:15 TheoFan
阅读(168)
评论(0)
推荐(0)
2023年6月10日
贪心算法(Greedy Algorithm)
摘要: ## 简介 (Introduction) > 贪心算法(又称贪婪算法)是指,在对问题求解时,总是做出在当前看来是最好的选择。也就是说,不从整体最优上加以考虑,算法得到的是在某种意义上的局部最优解。 > 贪心算法不是对所有问题都能得到整体最优解,关键是贪心策略的选择。 ## 描述(Descriptio
阅读全文
posted @ 2023-06-10 12:25 TheoFan
阅读(96)
评论(0)
推荐(0)
高精度算法 (High Accuracy Algorithm)
摘要: ## 简介(Introduction) > 高精度算法(High Accuracy Algorithm)是处理大数字的数学计算方法。在一般的科学计算中,会经常算到小数点后几百位或者更多,当然也可能是几千亿几百亿的大数字。一般这类数字我们统称为高精度数,高精度算法是用计算机对于超大数据的一种模拟加,减
阅读全文
posted @ 2023-06-10 12:20 TheoFan
阅读(446)
评论(0)
推荐(0)
双指针(Two Pointers)
摘要: ## 简介(Introduction) > 双指针算法是一种广泛运用的基础算法,在很多地方都有应用,双指针算法就是运用单调性使得指针只能单向移动。 ## 描述(Description) - 双指针算法是一种通过设置两个指针不断进行单向移动来解决问题的算法。 1. 首先写出最朴素的两层循环的写法 2.
阅读全文
posted @ 2023-06-10 12:13 TheoFan
阅读(74)
评论(0)
推荐(0)
离散化算法 (Discretization Algorithm)
摘要: ## 简介(Introduction) > 离散化 —— 把无限空间中有限的个体映射到有限的空间中去,以此提高算法的时空效率,即:在不改变数据相对大小的条件下,对数据进行相应的缩小。 >离散化本质上可以看成是一种 **哈希**,其保证数据在哈希以后仍然保持原来的 **全/偏序** 关系。 ## 描述
阅读全文
posted @ 2023-06-10 12:05 TheoFan
阅读(340)
评论(0)
推荐(0)
稀疏矩阵(Sparse Matrix)
摘要: ## 简介(Introduction) > 矩阵中,若数值为 $0$ 的元素数目 **远远多于** 非 $0$ 元素的数目,并且非 $0$ 元素分布没有规律时,则称该矩阵为稀疏矩阵;与之相反,若非 $0$ 元素数目占大多数时,则称该矩阵为稠密矩阵。 ## 描述(Description) 1. 当一个
阅读全文
posted @ 2023-06-10 11:26 TheoFan
阅读(221)
评论(0)
推荐(0)
下一页
公告