区间合并（Merge-Interval）

简介(Introduction)

区间合并就是将坐标轴中两个存在交集的区间合并成一个区间，是一种比较"狭窄"的算法

描述(Description)

1. 将所有区间按照左端点从小到大进行排序
2. 排完序后，当前区间和下一个区间的关系有三种：
   1. 下一个区间左右端点在当前区间内 —— 不用更新
   2. 下一个区间左端点在当前区间内，右端点在当前区间外 —— 当前区间的右端点更新
   3. 下一个区间左端点在当前区间外 —— 更新为下一个区间
3. 当前区间维护完毕，当前区间更新为下一个区间

示例(Example)

• 合并前五个区间：\((1, 2) (2, 4) (5, 6) (7, 8) (7, 9)\)
  

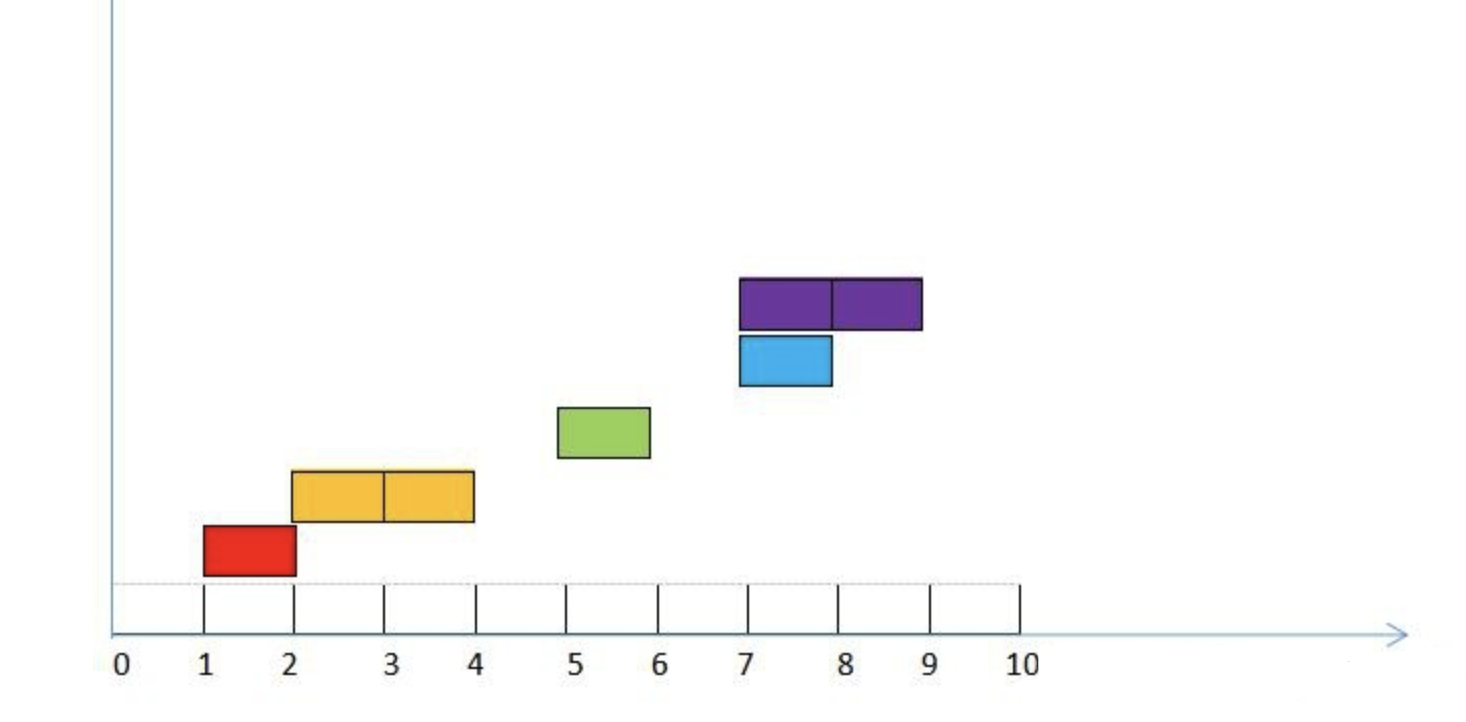
• 合并之后成为3个区间：\((1, 4) (5, 6) (7, 9)\)
  

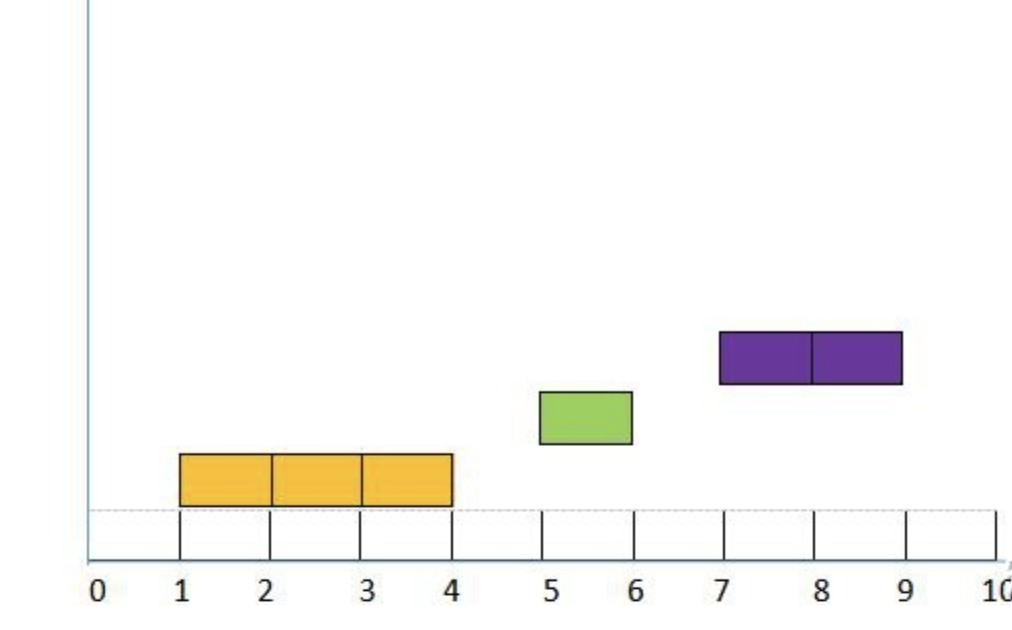
代码(Code)

// C++ Version

void merge_(vector<pii> &itvs) {
	vetor<pii> res;  //用来临时存合并后的区间

	sort(itvs.begin(), itvs.end());   //对数组起始坐标进行升序排序
	int st = -2e9, ed = -2e9;   //无穷小初始化 ———— ed代表区间结尾，st代表区间开头

	for (const auto &s: v) {
		if (ed < s.first) {     //两个区间没有交集
			if (st != -2e9) res.push_back({st, ed});
			st = s.first, ed = s.second;    //维护区间2
		} else ed = max(ed, s.second);  //两个区间有交集时，右侧坐标取两个区间中相对大的坐标
	}

	if (st != -2e9) res.push_back({st, ed});  //最后一组放入
	itvs = res; //还给itvs
}

---

应用(Application)

---

区间合并

---

给定 \(n\) 个区间 \([l, r]\)，要求合并所有有交集的区间。

注意如果在端点处相交，也算有交集。

输出合并完成后的区间个数。

例如：\([1, 3]\) 和 $ [2, 6] $可以合并为一个区间 \([1, 6]\)

输入格式

第一行包含整数 \(n\)

接下来 \(n\) 行，每行包含两个整数 \(l\) 和 \(r\)

输出格式

共一行，包含一个整数，表示合并区间完成后的区间个数。

数据范围

\(1 ≤ n ≤ 100000\)
\(−10^9 ≤ l ≤ r ≤ 10^9\)

输入样例：

5
1 2
2 4
5 6
7 8
7 9

输出样例：

3

• 题解：

  // C++ Version
  
  #include <bits/stdc++.h>
  
  using namespace std;
  
  typedef pair<int, int> pii;
  
  vector<pii> res, seg;
  int n;
  
  void merge_(vector<pii> &v) {
  	sort(v.begin(), v.end());   //对数组起始坐标进行升序排序
  	int st = -2e9, ed = -2e9;   //ed代表区间结尾，st代表区间开头（范围为负无穷）
  	for (const auto &s: v) {
  		if (ed < s.first) {     //两个区间没有交集
  			if (st != -2e9) res.push_back({st, ed});
  			st = s.first, ed = s.second;    //维护区间2
  		} 
  		else ed = max(ed, s.second);  //两个区间有交集时，右侧坐标取两个区间中相对大的坐标
  
  	}
  	if (st != -2e9) res.push_back({st, ed});
  	//考虑循环结束时的st,ed变量，此时的st,ed变量不需要继续维护，只需要放进res数组即可。
  	//因为这是最后的一个序列，所以不可能继续进行合并。
  }
  
  int main() {
  	scanf("%d", &n);
  	while (n -- ) {
  		int a, b;
  		scanf("%d%d", &a, &b);
  		seg.push_back({a, b});
  	}
  	merge_(seg);
  	cout << res.size() << endl;
  	return 0;
  }
  

---