离散化算法 (Discretization Algorithm)

简介(Introduction)

离散化 —— 把无限空间中有限的个体映射到有限的空间中去，以此提高算法的时空效率，即：在不改变数据相对大小的条件下，对数据进行相应的缩小。
离散化本质上可以看成是一种 哈希，其保证数据在哈希以后仍然保持原来的 全/偏序 关系。

描述(Description)

• 离散化用于处理一些个数不多，但是数据本身很大但是仍需要作为数组等无法过大的下标时，我们可以处理一下这些大的下标，并且依然保持其原序。
• 通俗地讲就是当有些数据因为本身很大或者类型不支持，自身无法作为数组的下标来方便地处理，而影响最终结果的只有元素之间的相对大小关系时，我们可以将原来的数据按照从大到小编号来处理问题

Tips:
      1. 注意去重复元素
      2. 快速保序映射

示例(Example)

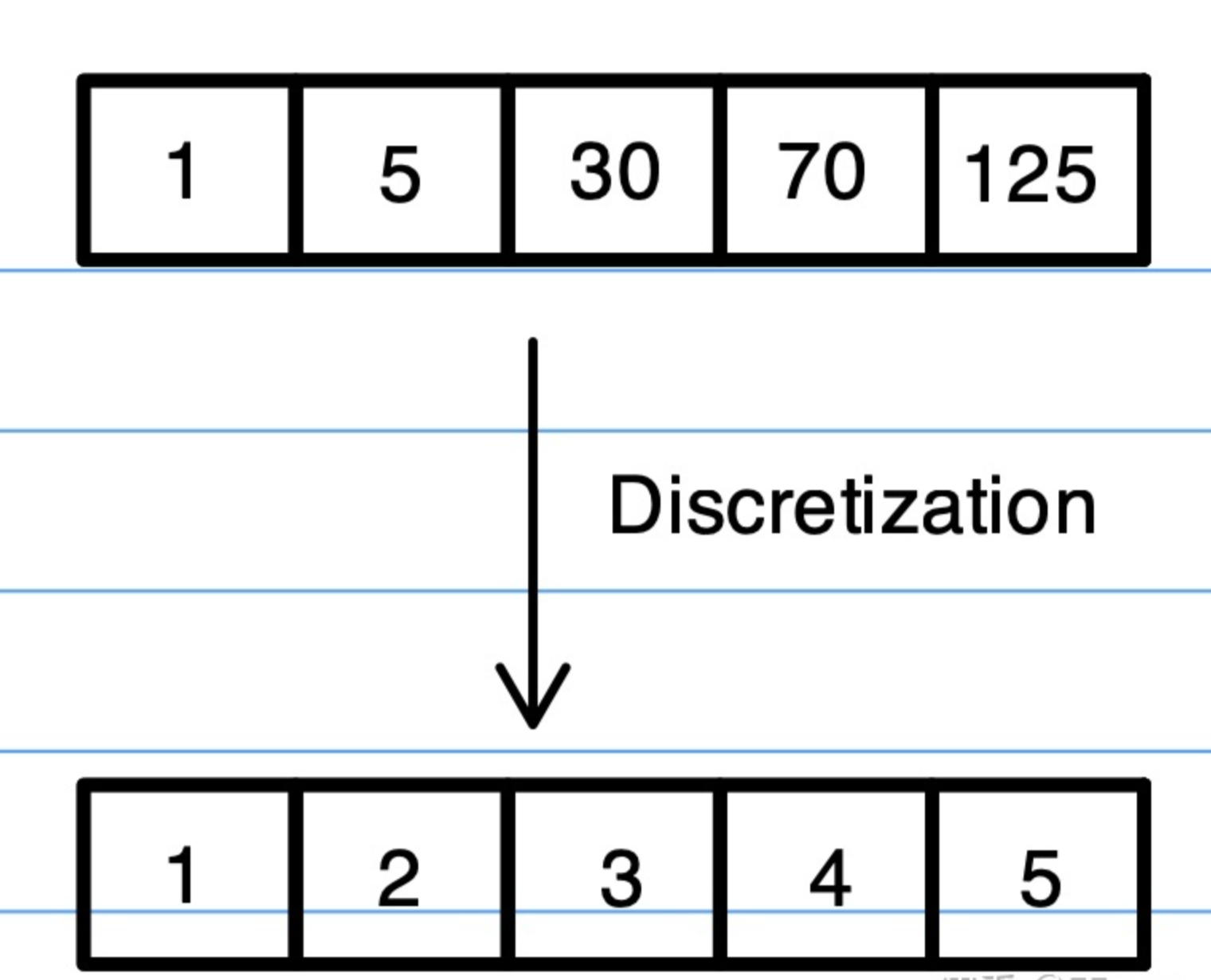
代码(Code)

1. 排序：
   sort(a.begin(), a.end());
2. 去重：
   a.erase(unique(a.begin(), a.end()), a.end());
3. 查找：
   • 使用 std::lower_bound 函数查找离散化之后的排名（即，新编号）：
     lower_bound(a + 1, a + len + 1, x) - a; // 查询 x 离散化后对应的编号
   • 二分查找：

     int find(int x) {
     	int l = 0 , r = a.size() -1;
     	while (l < r) {
     		int mid = l + r >> 1;
     		if (a[mid] >= x) r = mid;
     		else l = mid + 1;
     	}
     	return l + 1;	// 从1 ~ n的映射。
     }
     

应用(Application)

---

区间和

---

假定有一个无限长的数轴，数轴上每个坐标上的数都是 \(0\)
现在，我们首先进行 \(n\) 次操作，每次操作将某一位置 \(x\) 上的数加 \(c\) 。
接下来，进行 \(m\) 次询问，每个询问包含两个整数 \(l\) 和 \(r\) ，你需要求出在区间 \([l,r]\) 之间的所有数的和。

输入格式

第一行包含两个整数 \(n\) 和 \(m\) 。 接下来 \(n\) 行，每行包含两个整数 \(x\) 和 \(c\) 。 再接下里 \(m\) 行，每行包含两个整数 \(l\) 和 \(r\) 。

输出格式

共 \(m\) 行，每行输出一个询问中所求的区间内数字和。

数据范围

\(−10^9\le x \le 10^9 ,\)
\(1 \le n,\ m\le 10^5,\)
\(−10^9 \le l \le r \le 10^9,\)
\(−10000 \le c \le 10000\)

输入样例：

3 3
1 2
3 6
7 5
1 3
4 6
7 8

输出样例：

8
0
5

• 分析：
  • 由于坐标数据范围很大，但是数据量较小，考虑离散化处理所有坐标
  • 最后要求区间和，可以使用前缀和来求
• 题解：

  // C++ Version
  
  #include <iostream>
  #include <algorithm>
  
  using namespace std;
  
  typedef pair<int, int> pii;
  
  const int N = 3e5 + 10;
  
  int n, m;
  int a[N]; //用于前缀和计算
  
  vector<pii> add, query;  //用于存储输入
  vector<int> all;  //用于存储所有目标下标
  
  /**
   * 二分查找
   * @param x target
   * @return 从1 ~ n的映射，返回值需要加1
   */
  int find(int x) {
  	int l = 0, r = all.size() - 1;
  	while (l < r) {
  		int mid = l + r >> 1;
  		if (all[mid] >= x) r = mid;
  		else l = mid + 1;
  	}
  	return l + 1;
  }
  
  int main() {
  	scanf("%d%d", &n, &m);
  	for (int i = 0; i < n; i ++ ) {
  		int a, b;
  		scanf("%d%d", &a, &b);
  		add.push_back({a, b});
  		all.push_back(a);  // 将有用的下标全部存入all
  	}
  
  	for (int i = 0; i < m; i ++ ) {
  		int a, b;
  		scanf("%d%d", &a, &b);
  		query.push_back({a, b});
  
  		all.push_back(a);
  		all.push_back(b);
  	}
  
  	//排序
  	sort(all.begin(), all.end());
  
  	//去重
  	all.erase(unique(all.begin(), all.end()), all.end());
  
  	//插入数据
  	for (auto &item: add) {
  		a[find(item.first)] += item.second; //映射
  	}
  
  	//预处理前缀和
  	for (int i = 1; i <= all.size(); i ++ ) a[i] += a[i - 1]; //前缀和
  
  	//查询
  	for (auto &item: query) {
  	  cout << a[find(item.second)] - a[find(item.first) - 1] << endl;
  	}
  
  	return 0;
  }
  

---

补充(Supplement)

• 对 \(vector\) 进行离散化：

  vector<int> a, b;  // b 是 a 的一个副本
  sort(a.begin(), a.end());
  a.erase(unique(a.begin(), a.end()), a.end());
  for (int i = 0; i < n; ++i)
  	b[i] = lower_bound(a.begin(), a.end(), b[i]) - a.begin();
  

• 对 \(map\) 映射进行离散化：

  • 可以用 \(map\) （每次在 \(map\) 中查询一下这个值是否存在，如果存在则返回对应的值，否则对应另一个值）或 \(hash\) 表（即 \(unordered\_map\) 或手写 \(hash\) 表，运用方式和 \(map\) 相同）。

\(unordered\_map\) 与 \(map\) 的区别：

• 对于 \(map\) 的底层原理，是通过红黑树（一种非严格意义上的平衡二叉树）来实现的，\(map\) 内部所有的数据都是 有序 的（默认按 \(key\) 进行升序排序）

• \(unordered\_map\) 和 \(map\) 类似，都是存储的 \(key-value\) 的值，可以通过 \(key\) 快速索引到 \(value\)。不同的是 \(unordered\_map\) 不会 根据 \(key\) 的大小进行排序，存储时是根据 \(key\) 的 \(hash\) 值判断元素是否相同，即 \(unordered\_map\) 内部元素是无序的。\(unordered\_map\) 的底层是一个防冗余的哈希表（开链法避免地址冲突）

时间复杂度：\(O(\log n)\)