前缀和（Prefix Sum）

前缀和可以简单理解为「数列的前 \(n\) 项的和」，是一种重要的预处理方式，能大大降低查询的时间复杂度。

C++ 标准库中实现了前缀和函数 std::partial_sum，定义于头文件 <numeric> 中

---

一维前缀和(One-dimensional)

---

描述(Description)

• 递推:
  • 当 \(i = 0\) 时，\(sum[0] = a[0]\)
  • 当 \(i \ge 0\) 时，\(sum[i] = sum[i - 1] + a[i]\)

示例(Example)

初始数列：\([1, 2, 3, 4, 5]\)，前缀和处理后： \([1, 3, 6, 10, 15]\)

代码(Code)

• 前缀和：

  // C++ Version
  int a[N], s[N];
  for (int i = 1; i <= n; i ++ ) {
  	scanf("%d", &a[i]);  // 避免特判下标从1开始进行计算，一般定义i从1开始，0号元素为0
  	s[i] = s[i - 1] + a[i];
  }
  

  
  
• 查询 \((a, b)\) 区间内的前缀和

  int calc (int a, int b) {
  	return s[b] - s[a - 1];  // 查询 (a, b) 区间内的前缀和
  }
  

---

二维前缀和(Two-dimensional)

---

描述(Description)

• 二维前缀和的普通求解方法基于 容斥原理
  
  

示例(Example)

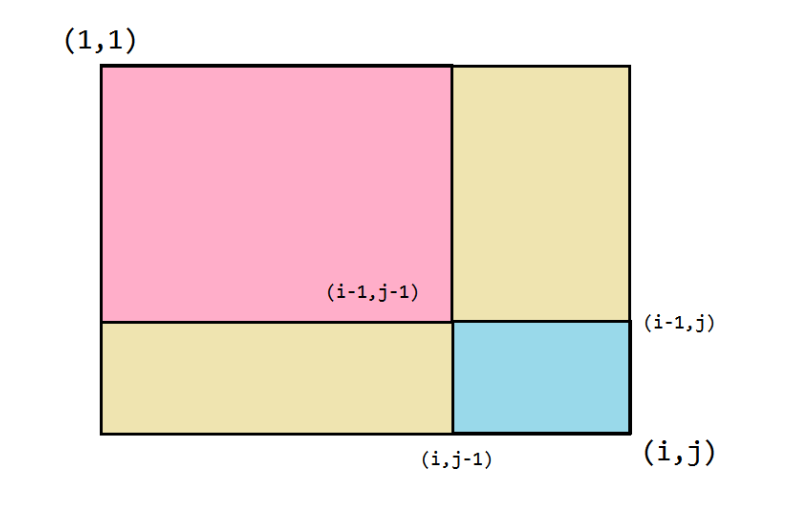
递推式为：$$s[i][j] = s[i - 1][j] + s[i][j - 1]-s[i - 1][j - 1] + a[i][j]$$
区间 \((x_1,y_1),(x_2,y_2)\) 之和为：$$s[x_2][y_2] - s[x_2][y_1-1]-s[x_1-1][y_2]+s[x_1-1][y_1-1]$$

代码(Code)

// C++ Version
void pre_sum (int a[][],int s[][],int n, int m) {
	for(int i = 1; i <= n; i ++ )
		for(int j = 1; j <= m; j ++ )
			s[i][j] = s[i][j - 1] + s[i - 1][j] - s[i - 1][j - 1] + a[i][j];
}

---