二分图（Bipartite Graph）

简介(Introduction)

二分图又称作二部图，是图论中的一种特殊模型。 设 \(G=(V,E)\) 是一个无向图，如果顶点 \(V\) 可分割为两个互不相交的子集 \((A,B)\)，并且图中的每条边 \((i,j)\) 所关联的两个顶点 \(i\) 和 \(j\) 分别属于这两个不同的顶点集 \((i\in A, j\in B)\)，则称图 \(G\) 为一个二分图。

描述(Description)

• 二分图即把图分为两个集合，集合内部没有边。
• 如果是二分图，一定没有奇数环
• 如果没有奇数环，一定是二分图
• 判断二分图常用的两个算法：
  1. 染色法
  2. 匈牙利算法
• 染色法 判断一个图是不是二分图。
  • 如果二分图能够被完美染色，那么它就是二分图，否则不是。染色的过程可以用 \(DFS\) 完成。
  • 对于某一个点，我们把他染色为 \(A\)，那么第一个和它相邻的点的颜色就染色为 \(B\)，下一个是 \(A\)，以此类推，可知该条通路上的所有点的颜色都确定。

时间复杂度：\(O(n + m)\)

示例(Example)

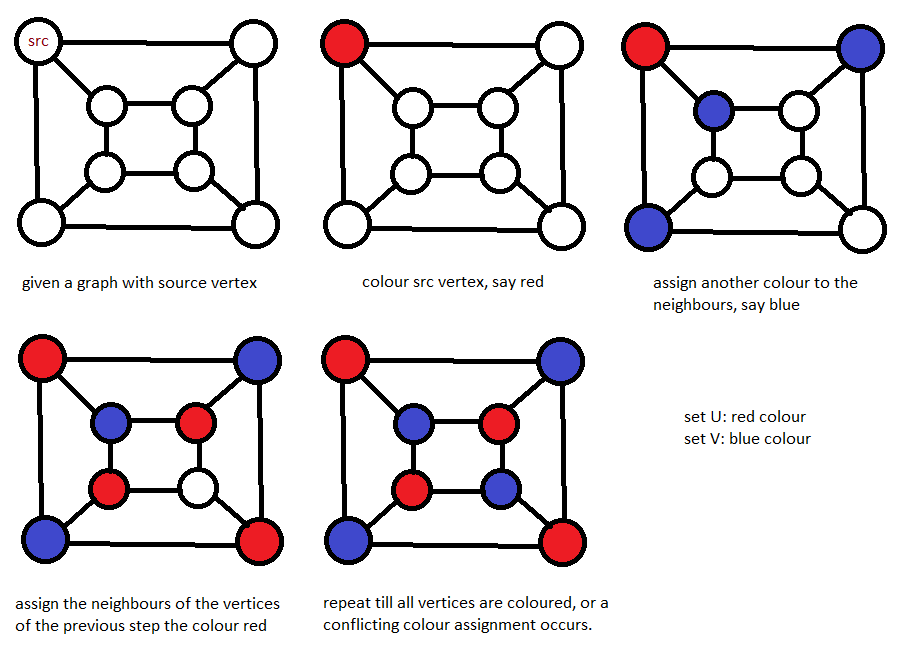
代码(Code)

// C++ Version

bool dfs(int u, int c) {
	color[u] = c;
	for (int i = h[u]; ~i; i = ne[i]) {  // 稀疏图用邻接表存储。
		int j = e[i];
		if (!color[j]) {  // 没染
			if (!dfs(j, 3 - c)) return false;  // 染色 1 和 2 交替。
		}
		else if (color[j] == c) return false;  // 染过
	}
	return true;
}

应用(Application)

---

染色法判断二分图

---

给定一个n个点m条边的无向图，图中可能存在重边和自环。
请你判断这个图是否是二分图。

输入格式

第一行包含两个整数 \(n\) 和 \(m\)。
接下来 \(m\) 行，每行包含两个整数 \(u\) 和 \(v\)，表示点 \(u\) 和点 \(v\) 之间存在一条边。

输出格式

如果给定图是二分图，则输出Yes，否则输出No。

数据范围

\(1 \le n, m \le 10^5\)

输入样例：

4 4
1 3
1 4
2 3
2 4`

输出样例：

Yes

• 题解：

  // C++ Version
  
  #include <cstdio>
  #include <cstring>
  
  using namespace std;
  
  const int N = 1e6 + 10;
  const int M = 2e6 + 10;
  
  int e[M], ne[M], h[M], idx;
  int color[N];
  int n, m;
  
  void add(int a, int b) {
  	e[idx] = b, ne[idx] = h[a], h[a] = idx++;
  }
  
  bool dfs(int t, int c) {
  	color[t] = c;
  
  	for (int i = h[t]; ~i; i = ne[i]) {
  		int j = e[i];
  		if (!color[j]){
  			if (!dfs(j, 3 - c)) return false;
  		}else if (color[j] == c) return false;
  	}
  	return true;
  }
  
  int main() {
  	scanf("%d%d", &n, &m);
  	memset(h, -1, sizeof h);
  	while (m -- ) {
  		int a, b;
  		scanf("%d%d", &a, &b);
  		add(a, b);
  		add(b, a);
  	}
  
  	bool flag = true;
  	for (int i = 1; i <= n; i ++ ) {
  		if (!color[i]) {
  			if (!dfs(i, 1)) {
  				flag = false;
  				break;
  			}
  		}
  	}
  
  	if (flag) puts("Yes");
  	else puts("No");
  	return 0;
  }
  

---