差分约束（Difference Constraints）

简介(Introduction)

如果一个系统由 \(n\) 个变量和 \(m\) 个约束条件组成，形成 \(m\) 个形如 \(a_i-a_j \le k\) 的不等式 \((i,j\in[1,n],k为常数)\),则称其为 差分约束

差分约束是求解关于一组变量的特殊不等式组的方法

描述(Description)

1. 先将每个不等式 \(x_i \le x_j + c\)，转化成一条从 \(x_j\) 走到 \(x_i\)，长度为 \(c\) 的一条边
2. 使用 超级源点，使得该源点一定可以遍历到所有边
   • 源点需要满足的条件：从源点出发，一定可以走到所有的边
3. 从源点求一遍单源最短路
   • 结果1：如果存在负环，则原不等式组一定无解
   • 结果2：如果没有负环，则 \(dist[i]\) 就是原不等式组的一个可行解

Tips:

• 如果求的是最小值，则应该求最长路；如果求的是最大值，则应该求最短路

• 最小值求最长路，\(dist\) 初始化为 \(-INF\)，更新条件为 \(dist[j]＜ dis[t] + w[i]\)

• 最大值求最短路，\(dist\) 初始化为 \(INF\)，更新条件为 \(dist[j]＞dist[t] + w[i]\)

• 若 \(x_i<c (c为常数)\) 可以建立一个超级源点 \(0\)，然后建立 \(0\to i\)， 长度是 \(c\) 的边即可

示例(Example)

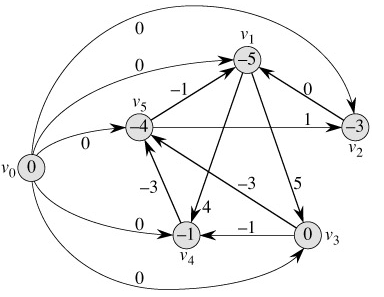
应用(Application)

---

糖果

---

幼儿园里有 \(N\) 个小朋友，老师现在想要给这些小朋友们分配糖果，要求每个小朋友都要分到糖果。

但是小朋友们也有嫉妒心，总是会提出一些要求，比如小明不希望小红分到的糖果比他的多，于是在分配糖果的时候， 老师需要满足小朋友们的 \(K\) 个要求。

幼儿园的糖果总是有限的，老师想知道他至少需要准备多少个糖果，才能使得每个小朋友都能够分到糖果，并且满足小朋友们所有的要求。

输入格式

输入的第一行是两个整数 \(N,K\)。

接下来 \(K\) 行，表示分配糖果时需要满足的关系，每行 \(3\) 个数字 \(X,A,B\)。

• 如果 \(X = 1\)．表示第 \(A\) 个小朋友分到的糖果必须和第 \(B\) 个小朋友分到的糖果一样多。
• 如果 \(X = 2\)，表示第 \(A\) 个小朋友分到的糖果必须少于第 \(B\) 个小朋友分到的糖果。
• 如果 \(X = 3\)，表示第 \(A\) 个小朋友分到的糖果必须不少于第 \(B\) 个小朋友分到的糖果。
• 如果 \(X = 4\)，表示第 \(A\) 个小朋友分到的糖果必须多于第 \(B\) 个小朋友分到的糖果。
• 如果 \(X = 5\)，表示第 \(A\) 个小朋友分到的糖果必须不多于第 \(B\) 个小朋友分到的糖果。

小朋友编号从 \(1\) 到 \(N\)。

输出格式

输出一行，表示老师至少需要准备的糖果数，如果不能满足小朋友们的所有要求，就输出 \(-1\)。

数据范围

\(1 \le N < 10^5\),
\(1 \le K \le 10^5\),
\(1 \le X \le 5\),
\(1 \le A,B \le N\),

输入数据完全随机。

输入样例：

5 7
1 1 2
2 3 2
4 4 1
3 4 5
5 4 5
2 3 5
4 5 1

输出样例：

11

• 题解：

  // C++ Version
  
  #include <cstdio>
  #include <cstring>
  #include <iostream>
  #include <algorithm>
  
  using namespace std;
  
  typedef long long ll;
  
  const int N = 1e5 + 10, M = 3 * N;
  
  int n, m;
  int h[N], e[M], w[M], ne[M], idx;
  bool st[N];
  int q[N], cnt[N];
  ll dist[N];
  
  void add(int a, int b, int c) {
  	e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx ++ ;
  }
  
  bool spfa() {
  	memset(dist, -0x3f, sizeof dist);
  	memset(st, 0, sizeof st);
  	memset(cnt, 0, sizeof cnt);
  
  	int hh = 0, tt = 1;
  	q[0] = 0;
  	dist[0] = 0;
  	st[0] = true;
  
  	int count = 0;
  
  	while (hh != tt) {
  		int t = q[-- tt];
  		st[t] = false;
  
  		for (int i = h[t]; ~i; i = ne[i]) {
  			int j = e[i];
  			if (dist[j] < dist[t] + w[i]) {
  				dist[j] = dist[t] + w[i];
  				cnt[j] = cnt[t] + 1;
  				if (cnt[j] >= n + 1) return false;
  				if (!st[j]) {
  					st[j] = true;
  					q[tt ++ ] = j;
  				}
  			}
  		}
  	}
  	return true;
  }
  
  int main() {
  	scanf("%d%d", &n, &m);
  	memset(h, -1, sizeof h);
  
  	for (int i = 1; i <= n; i ++ ) add(0, i, 1);
  	while (m -- ) {
  		int x, a, b;
  		scanf("%d%d%d", &x, &a, &b);
  		if (x == 1) add(a, b, 0), add(b, a, 0);
  		else if (x == 2) add(a, b, 1);
  		else if (x == 3) add(b, a, 0);
  		else if (x == 4) add(b, a, 1);
  		else if (x == 5) add(a, b, 0);
  	}
  
  	ll res = 0;
  	if (!spfa()) puts("-1");
  	else {
  		for (int i = 1; i <= n; i ++ ) res += dist[i];
  		cout << res << endl;
  	}
  	return 0;
  }
  

---