最短路径（Shortest Path）

简介(Introduction)

最短路径问题是图论研究中的一个经典算法问题， 旨在寻找图（由结点和路径组成的）中两结点之间的最短路径。

描述(Description)

• 算法具体的形式包括：
  1. 确定起点的最短路径问题 - 即已知起始结点，求最短路径的问题。
  2. 确定终点的最短路径问题 - 与确定起点的问题相反，该问题是已知终结结点，求最短路径的问题。在无向图中该问题与确定起点的问题完全等同，在有向图中该问题等同于把所有路径方向反转的确定起点的问题。
  3. 确定起点终点的最短路径问题 - 即已知起点和终点，求两结点之间的最短路径。
  4. 全局最短路径问题 - 求图中所有的最短路径。

• 最短路径算法：
  • 单源最短路径：
    • 所有边权值都是正数：
      1. 朴素 \(Dijkstra\) 算法，时间复杂度：\(O(n^2)\)
      2. 堆优化 \(Dijkstra\) 算法，时间复杂度：\(O(m \log n)\)
    • 存在负权值的边：
      1. \(Bellman-Ford\) 算法，时间复杂度：\(O(n*m)\)
      2. \(SPFA\) 算法，时间复杂度：一般为 ：\(O(k*n)\)，最坏为：\(O(n*m)\)
  • 多源汇最短路径：\(Folyd\) 算法，时间复杂度：\(O(n^3)\)

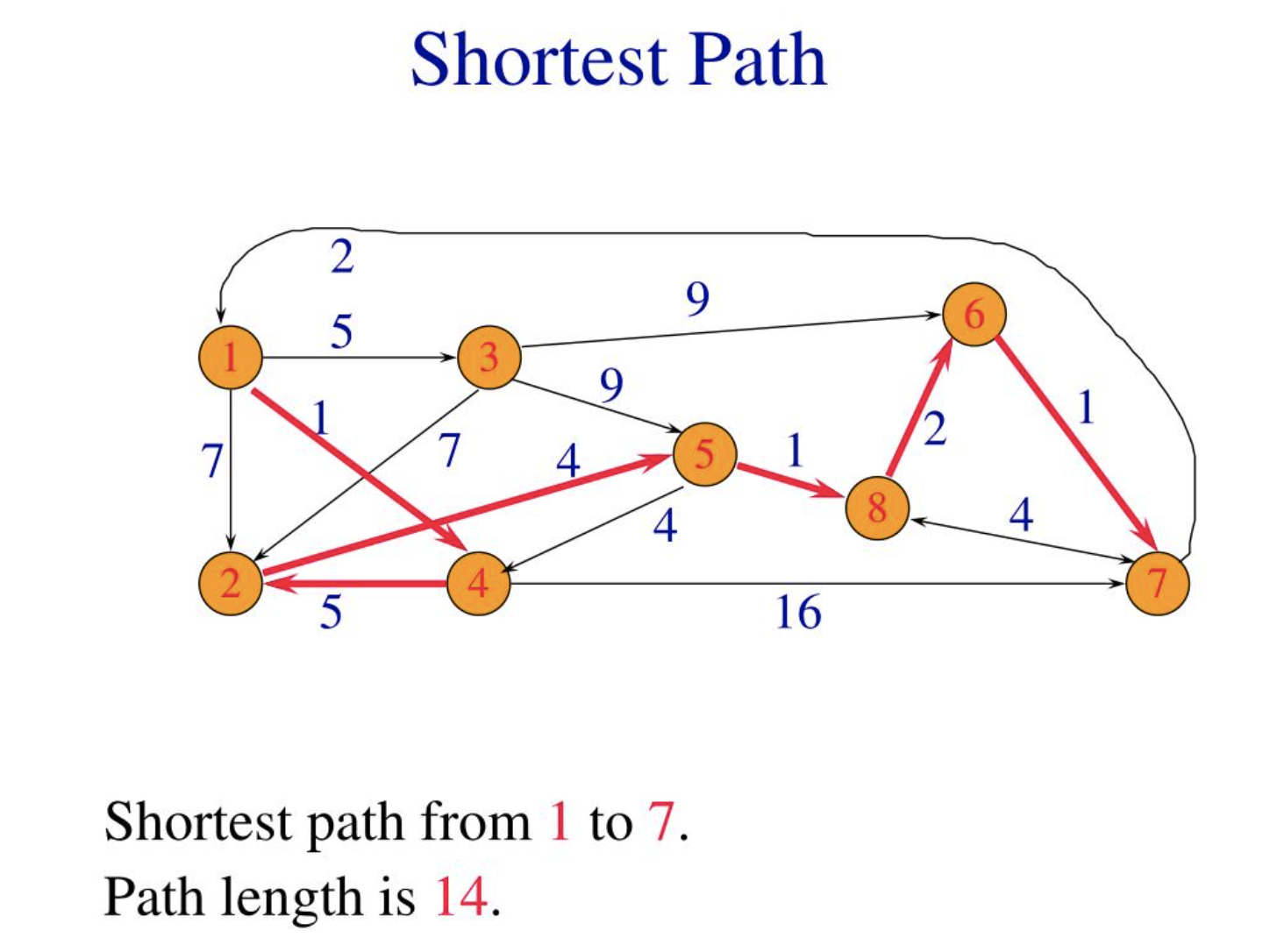
示例(Example)