最小生成树（Minimum Spanning Tree）

简介(Introduction)

一个有 \(n\) 个结点的连通图的生成树是原图的极小连通子图，且包含原图中的所有 \(n\) 个结点，并且有保持图连通的最少的边。

描述(Description)

• 在一给定的无向图 \(G = (V, E)\) 中，\((u, v)\) 代表连接顶点 \(u\) 与顶点 \(v\) 的边（即），而 \(w(u, v)\) 代表此边的权重，若存在 \(T\) 为 \(E\) 的子集且为无循环图，使得联通所有结点的的 \(w(T)\) 最小，则此 \(T\) 为 \(G\) 的 最小生成树(MST)

定理
        任意一棵最小生成树一定包含无向图权值最小的边。

证明：
        反证法。假设无向图 \(G = (V, E)\) 存在一棵最小生成树不包含权值最小的边。设 \(e=(x, y, z)\) 时无向图中权值最小的边。
把 \(e\) 添加到树中， \(e\) 会和树上从 \(x\) 到 \(y\) 的路径一起构成一个环，且环上其他边的权值都比 \(z\) 大。
因此，用 \(e\) 代替环上的其他任意一条边，会形成一课权值和更小的生成树，与假设矛盾。
故假设不成立，原命题成立。
        证毕。

推论
        给定一张无向图 \(G = (V, E), n=|V|,m=|E|\)。从区中选出 \(k < n - 1\) 条边构成 \(G\) 的一个生成森林。若再从剩余的 \(m-k\) 条边中选 \(n-1-k\) 条添加到生成森林中，使其成为 \(G\) 的生成树，并且选出的边的权值之和最小，则该生成树一定包含这 \(m-k\) 条边中连接生成森林的两个不连通节点的权值最小的边。

• 求解：
  1. 无向图（常见）：
     • \(Prim\)：一般用于 稠密图
     • \(Kruskal\)：一般用于 稀疏图
  2. 有向图：朱刘算法

示例(Example)

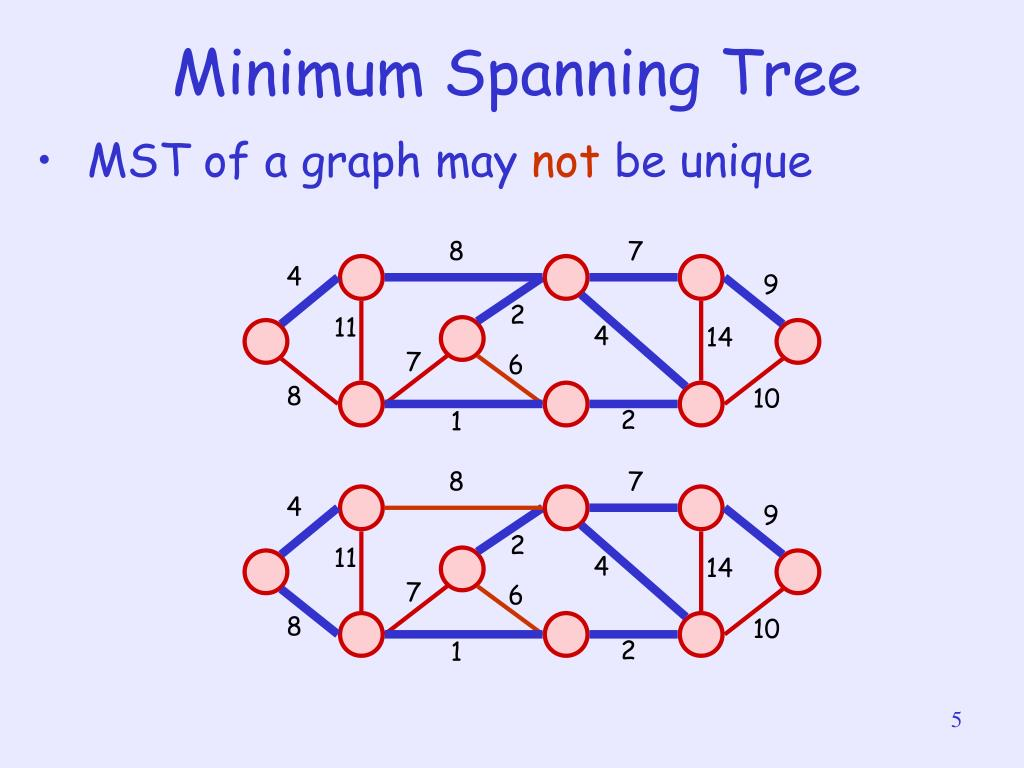
应用(Application)

例如： 要在 \(n\) 个城市之间铺设光缆，主要目标是要使这 \(n\) 个城市的任意两个之间都可以通信，但铺设光缆的费用很高，且各个城市之间铺设光缆的费用不同，因此另一个目标是要使铺设光缆的总费用最低。