SPFA Algorithm
简介(Introduction)
\(SPFA\) 算法是 \(Bellman-Ford\) 算法的 队列优化 算法的别称,通常用于 求含负权边的单源最短路径,以及 判负权环
描述(Description)
-
\(SPFA\) 算法是对 \(Bellman-Ford\) 算法的优化。\(Bellman-Ford\) 算法在每次更新时,遍历了所有的边,但每次遍历不一定都会更新最短路径
-
判断负环:
- 统计每个点入队的次数,如果某个点入队 \(n\) 次,说明存在负环
-
\(SPFA\) 算法流程:
- 建立一个队列,最初队列中只含有起点 \(1\)
- 去出队头节点 \(x\),扫描他的所有出边 \((x, y, w)\),若 \(dist[y] > dist[x] + w\),则用 \(dist[x] + w\) 更新 \(dist[y]\)。同时,若 \(y\) 不再队列中,则将 \(y\) 入队
- 重复上述步骤,直至队列为空
时间复杂度:
-
一般:\(O(km)\) ( \(k\) 为系数,\(m\) 为边数)
-
最坏:\(O(nm)\) ( \(n\) 为点数,\(m\) 为边数)
Hint:- 若 \(n\times m\) 较大时,需使用 堆优化的 \(Dijkstra\) 进行求解
- 在寻找负环时将 队列换成栈(\(BFS\) 变成 \(DFS\)) 可能具有更高效率,但最坏时间复杂度仍然为指数级。
示例(Example)
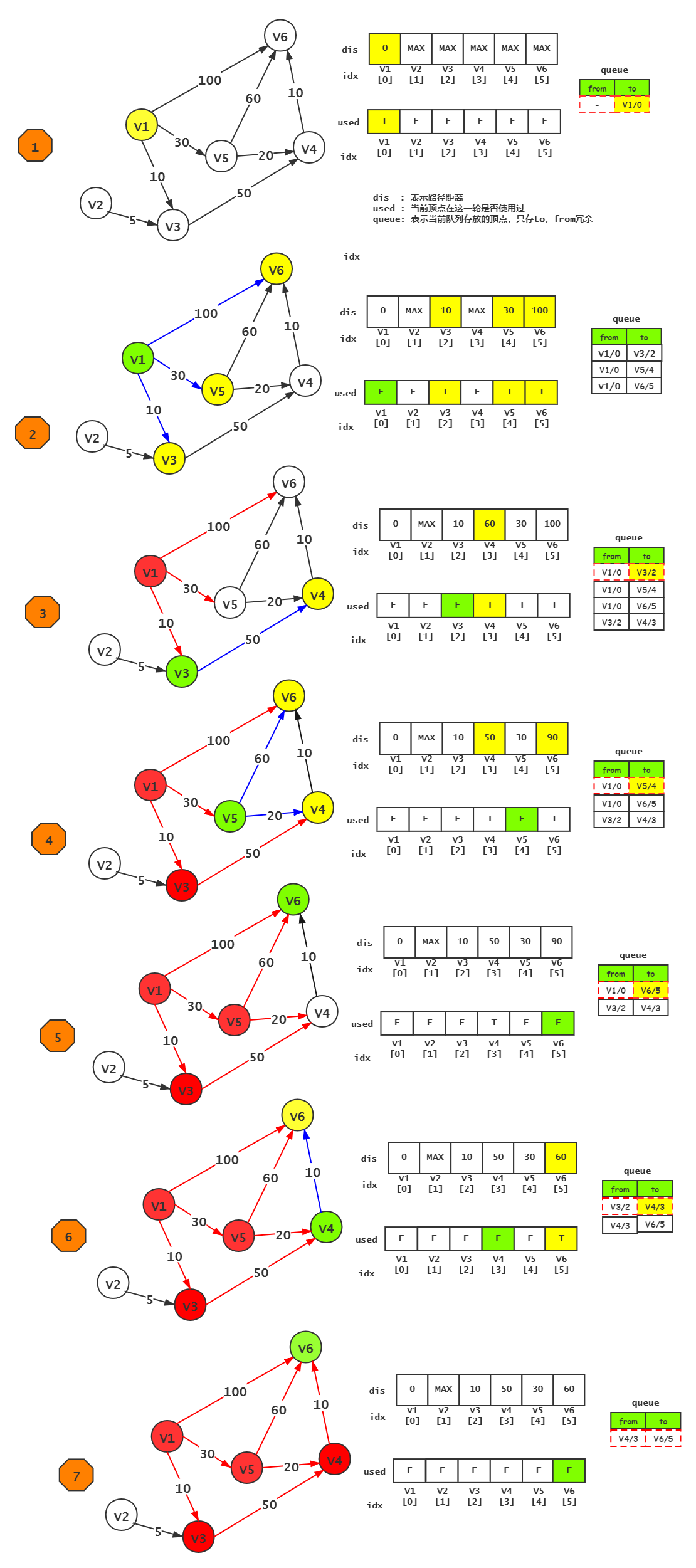
代码(Code)
// C++ Version
int dist[N]; // 记录最短路径
bool st[N]; // st 数组用于判断这个点是不是已经在队列中。已经在队列中就不必再加入进来。
int q[N]; // 定义队列
void spfa() {
memset(dist, 0x3f, sizeof dist);
int hh = 0, tt = 1;
q[0] = 1, st[1] = true;
dist[1] = 0;
while (hh != tt) {
int t = q[hh ++ ];
if (hh == N) hh = 0;
st[t] = false;
for (int i = h[t]; ~i; i = ne[i]) {
int j = e[i];
if (dist[j] > dist[t] + w[i]) {
dist[j] = dist[t] + w[i];
if (!st[j]) { // 如果 j 不再队列中
q[tt ++ ] = j;
if (tt == N) tt = 0;
st[j] = true;
}
}
}
}
}
应用(Application)
热浪
德克萨斯纯朴的民众们这个夏天正在遭受巨大的热浪!!!
他们的德克萨斯长角牛吃起来不错,可是它们并不是很擅长生产富含奶油的乳制品。
农夫John此时身先士卒地承担起向德克萨斯运送大量的营养冰凉的牛奶的重任,以减轻德克萨斯人忍受酷暑的痛苦。
John已经研究过可以把牛奶从威斯康星运送到德克萨斯州的路线。
这些路线包括起始点和终点一共有 \(T\) 个城镇,为了方便标号为 \(1\) 到 \(T\)。
除了起点和终点外的每个城镇都由 双向道路 连向至少两个其它的城镇。
每条道路有一个通过费用(包括油费,过路费等等)。
给定一个地图,包含 \(C\) 条直接连接 \(2\) 个城镇的道路。
每条道路由道路的起点 \(R_s\),终点 \(R_e\) 和花费 \(C_i\) 组成。
求从起始的城镇 \(T_s\) 到终点的城镇 \(T_e\) 最小的总费用。
输入格式
第一行: \(4\) 个由空格隔开的整数: \(T, C, T_s, T_e\);
第 \(2\) 到第 \(C+1\) 行: 第 \(i+1\) 行描述第 \(i\) 条道路,包含 \(3\) 个由空格隔开的整数: \(R_s, R_e, C_i\)。
输出格式
一个单独的整数表示从 \(T_s\) 到 \(T_e\) 的最小总费用。
数据保证至少存在一条道路。
数据范围
\(1 \le T \le 2500\) ,
\(1 \le C \le 6200\) ,
\(1 \le T_s,T_e,R_s,R_e \le T\) ,
\(1 \le C_i \le 1000\)
输入样例:
7 11 5 4
2 4 2
1 4 3
7 2 2
3 4 3
5 7 5
7 3 3
6 1 1
6 3 4
2 4 3
5 6 3
7 2 1
输出样例:
7
- 题解:
// C++ Version #include <cstdio> #include <iostream> #include <algorithm> #include <cstring> #include <queue> using namespace std; const int N = 2510, M = 6200 * 2 + 10; int n, m, S, T; int h[N], e[M], ne[M], w[M], idx; int dist[N]; int st[N]; void add(int a, int b, int c) { e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx ++ ; } void spfa() { memset(dist, 0x3f, sizeof dist); dist[S] = 0; queue<int> q; q.push(S); while (q.size()) { int t = q.front(); q.pop(); st[t] = false; // 出队后删除标记 for (int i = h[t]; ~i; i = ne[i]) { int j = e[i]; if (dist[j] > dist[t] + w[i]) { dist[j] = dist[t] + w[i]; if (!st[j]) { st[j] = true; q.push(j); } } } } } int main() { memset(h, -1, sizeof h); cin >> n >> m >> S >> T; while (m -- ) { int a, b, c; cin >> a >> b >> c; add(a, b, c); add(b, a, c); } spfa(); cout << dist[T] << endl; return 0; }
负环
给定一个 \(n\) 个点的有向图,请求出图中是否存在从顶点 \(1\) 出发能到达的负环。
负环的定义是:一条边权之和为负数的回路。
输入格式
本题单测试点有多组测试数据。
输入的第一行是一个整数 \(T\),表示测试数据的组数。对于每组数据的格式如下:
第一行有两个整数,分别表示图的点数 \(n\) 和接下来给出边信息的条数 \(m\)。
接下来 \(m\) 行,每行三个整数 \(u, v, w\)。
注意,\(m\) 不是图的边数。
- 若 \(w \geq 0\),则表示存在一条从 \(u\) 至 \(v\) 边权为 \(w\) 的边,还存在一条从 \(v\) 至 \(u\) 边权为 \(w\) 的边。
- 若 \(w < 0\),则只表示存在一条从 \(u\) 至 \(v\) 边权为 \(w\) 的边。
输出格式
对于每组数据,输出一行一个字符串,若所求负环存在,则输出
YES,否则输出NO。数据范围
\(1 \leq n \leq 2 \times 10^3\),\(1 \leq m \leq 3 \times 10^3\)
\(1 \leq u, v \leq n\),\(-10^4 \leq w \leq 10^4\)
\(1 \leq T \leq 10\)
样例输入
2
3 4
1 2 2
1 3 4
2 3 1
3 1 -3
3 3
1 2 3
2 3 4
3 1 -8
样例输出
NO
YES
- 题解:
#include <iostream> #include <cstring> #include <queue> using namespace std; const int N = 3010, M = N * 2; int n, m; int h[N], e[M], ne[M], w[M], idx; int dist[N], cnt[N]; bool st[N]; void add(int a, int b, int c) { e[idx] = b, ne[idx] = h[a], w[idx] = c, h[a] = idx++; } bool spfa() { memset(cnt, 0, sizeof cnt); memset(st, 0, sizeof st); memset(dist, 0x3f, sizeof dist); queue<int> q; q.push(1); st[1] = true, dist[1] = 0; while (q.size()) { int t = q.front(); q.pop(); st[t] = false; for (int i = h[t]; ~i; i = ne[i]) { int j = e[i]; if (dist[j] > dist[t] + w[i]) { dist[j] = dist[t] + w[i]; cnt[j] = cnt[t] + 1; if (cnt[j] >= n) return true; if (!st[j]) { q.push(j); st[j] = true; } } } } return false; } int main() { int T; cin >> T; while ( T -- ) { memset(h, -1, sizeof h); idx = 0; cin >> n >> m; for (int i = 0; i < m; i ++ ) { int a, b, c; cin >> a >> b >> c; add(a, b, c); if (c >= 0) add(b, a, c); } puts(spfa() ? "YES" : "NO"); } } return 0;


 浙公网安备 33010602011771号
浙公网安备 33010602011771号