Bellman-Ford Algorithm

简介(Introduction)

贝尔曼-福特算法 \((Bellman-Ford)\) 是由 理查德·贝尔曼和莱斯特·福特 创立的，求解 可能存在负环 的 有限路线单源最短路 问题的一种算法。

描述(Description)

• 其优于 \(Dijkstra\) 算法的方面是边的权值可以为 负数 解决了 \(Dijkstra\) 无法求的存在负权边的问题。
• 它的原理是对图进行 \(m - 1\) 次 松弛操作，得到所有可能的最短路径。
• 其实现方式是通过 \(m\) 次迭代求出从源点到终点 不超过 \(m\) 条边构成的最短路的路径。一般情况下要求途中不存在 负环。但是在边数有限制的情况下允许存在负环。

• 松弛

  • 每次松弛操作实际上是对相邻节点的访问，第次松弛操作保证了所有深度为 \(n\) 的路径最短。
  • 由于图的最短路径最长不会经过超过 \(m - 1\) 条边，所以可知 \(Bellman-Ford\) 算法所得为最短路径。

• 负边权操作

  • 与 \(Dijkstra\) 算法不同的是， \(Dijkstra\) 算法的基本操作“拓展”是在深度上寻路，而“松弛”操作则是在广度上寻路，这就确定了 \(Bellman-Ford\) 算法可以对负边进行操作而不会影响结果。

• 负权环判定：

  • 因为负权环可以无限制的降低总花费，所以如果发现第 \(n\) 次操作仍可降低花销，就一定存在负权环 —— 割巢原理

时间复杂度: \(O(nm)\)

示例(Example)

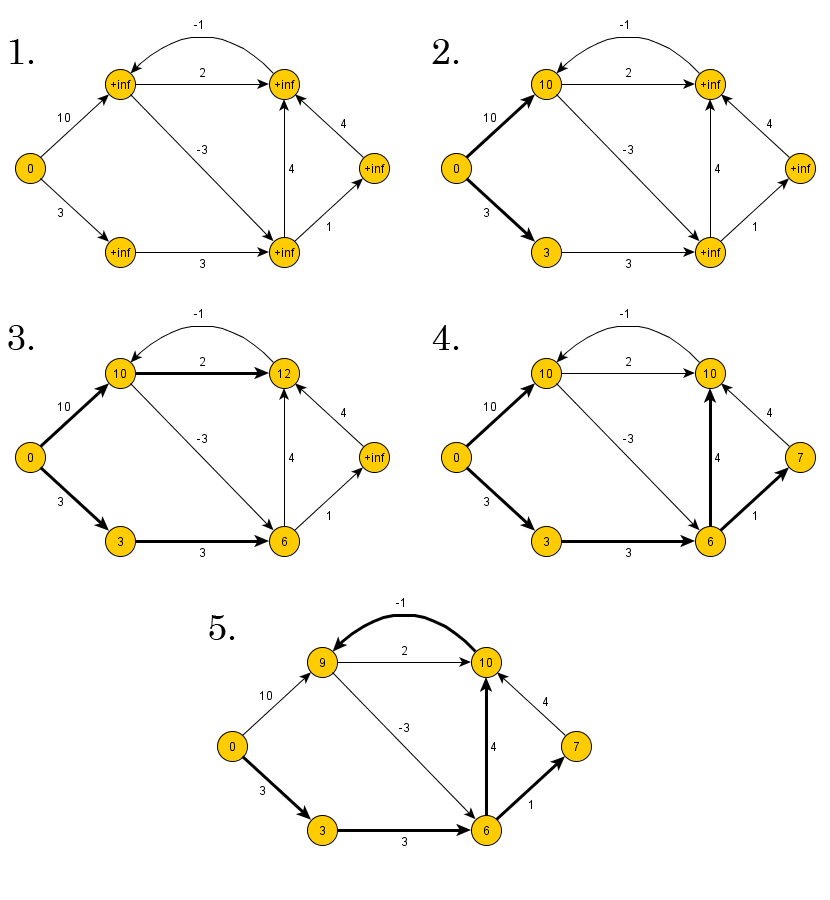
• 每次迭代都是在 上一次的基础上 进行的，因此我们在实现时要保留上一次的结果
• 理论中改变是同步完成的，但是实际上我们需要一个一个修改值。

代码(Code)

// C++ Version

int dist[MAXN], backup[MAXN];  // dist距离，backup用来存上一次的结果。

struct Edge {  //用来存边
	int a,  b;
	int w;
} edge[MAXM];

int Bellman_Ford() {
	memset(dist, 0x3f, sizeof dist);
	dist[1] = 0;  // 源点初始化
	for (int i = 0; i < k; i ++ ) {  // 遍历 k 次
		memcpy(backup, dist, sizeof dist);  // 存上一次答案。
		for (int j = 0; j < m; j ++ ) {  // 遍历所有边
			int a = Edge[j].a, b = Edge[j].b, w = Edge[j].w;
			dist[b] = min(dist[b], backup[a] + w);
		}
	}

	// 因为可能有负权边甚至是负环的存在，使得“正无穷”在迭代过程中受到一点影响。
	if (dist[n] > 0x3f3f3f3f / 2) return -1;  // 存在负环
	return dist[n];
}

应用(Application)

有边数限制的最短路

---

给定一个 \(n\) 个点 \(m\) 条边的有向图，图中 可能存在重边和自环，边权可能为负数。
请你求出从 \(1\) 号点到 $n $号点的最多经过 \(k\) 条边的最短距离，如果无法从 \(1\) 号点走到 \(n\) 号点，输出impossible。

注意：图中 可能存在负权回路。

输入格式

第一行包含三个整数 \(n，m，k\)

接下来 \(m\) 行，每行包含三个整数 \(x，y，z\) ，表示存在一条从点 \(x\) 到点 \(y\) 的有向边，边长为 \(z\)

输出格式

输出一个整数，表示从 \(1\) 号点到 \(n\) 号点的最多经过 \(k\) 条边的最短距离。
如果不存在满足条件的路径，则输出 impossible

数据范围

\(1 ≤ n, k ≤ 500\)

\(1 ≤ m ≤ 10000\)

任意边长的绝对值不超过 \(10000\)

输入样例：

3 3 1
1 2 1
2 3 1
1 3 3

输出样例：

3

• 分析：

  • 因为存在可能存在负权边，所以不能使用 \(Dijkstra\) 算法。
  • 本题给定了路径数 \(k\) 的限制，所以可以用 \(Bellman-Ford\) 算法来实现，若存在 负环，且 负环 不限路径数，答案就可能是 \(-INF\)，则不能使用 \(Bellman-Ford\) 算法

• 题解：

  // C++ Version
  
  #include <iostream>
  #include <cstring>
  
  using namespace std;
  
  const int N = 510, M = 10010;
  
  int n, m, k;
  int dist[N], backup[N]; //dist 存距离，backup用来存上一次的结果
  
  struct Edge {    //用于保存每一条边
  	int a, b, w;
  } edges[M];
  
  void bellman_ford() {
  	memset(dist, 0x3f, sizeof dist);// 初始化  dist
  	dist[1] = 0;
  
  	for (int i = 0; i < k; i ++ ) {
  		memcpy(backup, dist, sizeof dist);  // 拷贝数组记录下原数组的值
  		for (int j = 0; j < m; j ++ ) { // 遍历每一条边，更新边的值
  			int a = edges[j].a, b = edges[j].b, w = edges[j].w;
  			// 避免 a 更新后马上更新 b，使用 backup 数组中的原始数据，更新为最小值
  			dist[b] = min(dist[b], backup[a] + w);
  		}
  	}
  }
  
  int main() {
  	scanf("%d%d%d", &n, &m, &k);
  
  	for (int i = 0; i < m; i ++ ) {
  		int a, b, c;
  		scanf("%d%d%d", &a, &b, &c);
  		edges[i] = {a, b, c};
  	}
  
  	bellman_ford();
  
  	//因为可能有负权边甚至是负环的存在，使得“正无穷”在迭代过程中受到影响
  	//所以判断条件可以修改为dist[n]大于无穷大 除2
  	if (dist[n] > 0x3f3f3f3f / 2) puts("impossible");
  	else printf("%d\n", dist[n]);
  	return 0;
  }
  

---