Dijkstra Algorithm

简介(Introduction)

迪杰斯特拉算法 \((Dijkstra\ Algorithm)\) 是由荷兰计算机科学家克斯特拉 1959年提出的。是从一个顶点到其余各顶点的 最短路径 算法，解决的是 有权图中最短路径问题。
迪杰斯特拉算法主要特点是从起始点开始，采用 贪心算法 的策略，每次遍历到始点距离最近且未访问过的顶点的邻接节点，直到扩展到终点为止。

描述(Description)

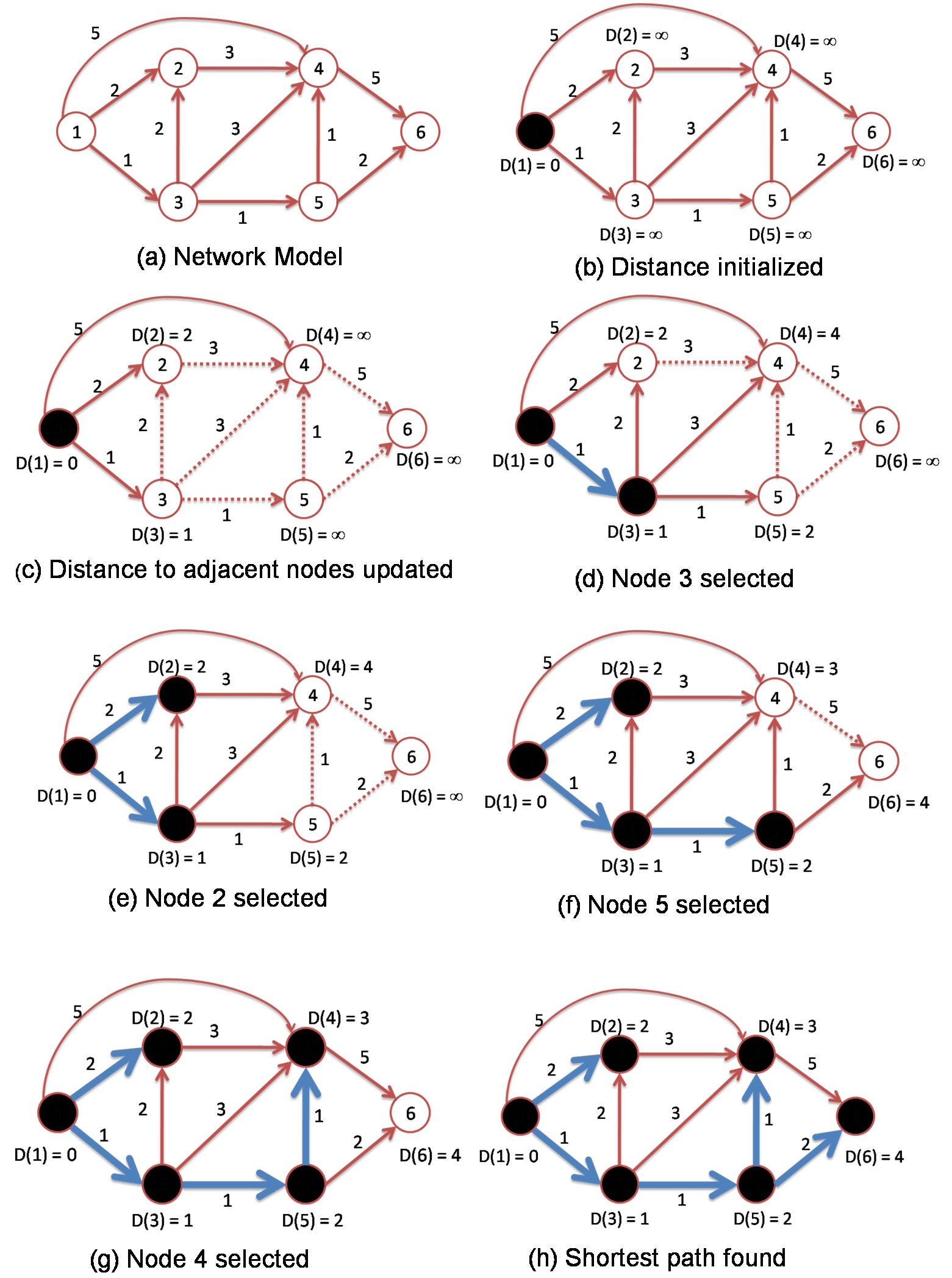
• \(Dijkstra\) 算法求的是 单源最短路 问题。其实现过程是这样的：
  1. 先把图中的所有点划分了两个集合 \(S\) 和 \(T\) 。\(S\) 表示 已经求得最短路 的顶点的集合，\(T\) 表示 还没有求得最短路 的顶点的集合。( 初始时源点与自身的距离为 \(0\) )
  2. 每次从集合 \(T\) 中选取一个点，这个点和源点的路径为 所有与源点直接相通的点的最小值。通过这个点更新源点和 \(T\) 中其他点的最短路径，然后把这个点加入到 \(S\) 中。
  3. 循环第二步操作，直到 \(T\) 中为空，说明所有点到源点的最短距离都已经求得，算法结束
     
     

Hint： \(Dijkstra\) 算法只适用于 边权均为正的图

示例(Example)

代码(Code)

• 朴素 \(Dijkstra\) —— 时间复杂度：\(O(n^2)\)

  // C++ Version
  
  int g[N][N];
  int dist[N];  // 存距离
  bool st[N];
  
  void init() {memset(g, 0x3f, sizeof g)};  // 初始化距离
  
  int dijkstra() {
  	memset(dist, 0x3f, sizeof dist);
  	dist[1] = 0;  // 源点初始化
  	for (int i = 0; i < n; i ++ ) // 找到最小距离
  		int t = -1;
  		for (int j = 1; j <= n; j ++ ) {
  			if (!st[j] && (t == -1 || dist[j] < dist[t]))
  				t = j;
  
  		st[t] = true;  // 放入 S 集合中
  		for (int j = 1; j <= n; j ++ )
  			dist[j] = min(dist[j], dist[t] + g[t][j]);  // 1 -> t + t -> j   更新 1 -> j;
  	}
  	if (dist[n] == 0x3f3f3f3f) return -1;
  	return dist[n];
  }
  

• 堆优化 \(dijkstra\) —— 时间复杂度：\(O(m \log n)\)

  // C++ Version
  
  void dijkstra() {
  	memset(dist, 0x3f, sizeof dist);
  	dist[s] = 0;
  	priority_queue<pii> heap;
  	heap.push({0, s});
  	while (heap.size()) {
  		auto t = heap.top();
  		heap.pop();
  
  		int no = t.y;
  		if (st[no]) continue;
  		st[no] = true;
  
  		for (int i = h[no]; ~i; i = ne[i]) {
  			int j = e[i];
  			if (dist[j] > dist[no] + w[i]) {
  				dist[j] = dist[no] + w[i];
  				if (!st[j]) heap.push({-dist[j], j});
  			}
  		}
  	}
  }
  

应用(Application)

---

单源最短路径

---

2018 年 7 月 19 日，某位同学在 NOI Day 1 T1 归程一题里非常熟练地使用了一个广为人知的算法求最短路。

然后呢？

\(100 \to 60\)

\(Ag \to Cu\)

最终，他因此没能与理想的大学达成契约。

小 F 衷心祝愿大家不再重蹈覆辙。

题目描述

给定一个 \(n\) 个点，\(m\) 条有向边的带非负权图，请你计算从 \(s\) 出发，到每个点的距离。

数据保证你能从 \(s\) 出发到任意点。

输入格式
第一行为三个正整数 \(n,m,s\)。 第二行起 \(m\) 行，每行三个非负整数 \(u_i, v_i, w_i\) 表示从 \(u_i\) 到 \(v_i\) 有一条权值为 \(w_i\) 有向边。

输出格式
输出一行 \(n\) 个空格分隔的非负整数，表示 \(s\) 到每个点的距离。

数据范围
\(1\le n \le 10^5\)
\(1\le m \le 2 * 10^5\)
\(s = 1\)
\(1 \le u_i, v_i \le n\)
\(0 \le w_i \le 10^9\)

输入样例：

4 6 1
1 2 2
2 3 2
2 4 1
1 3 5
3 4 3
1 4 4

输出样例

0 2 4 3

• 题解：

  #include <cstdio>
  #include <iostream>
  #include <cstring>
  #include <queue>
  
  #define x first
  #define y second
  
  using namespace std;
  
  typedef pair<int, int> pii;
  
  const int N = 100010, M = 500010;
  
  int n, m, s;
  int h[N], e[M], ne[M], w[M], idx;
  int dist[N];
  bool st[N];
  
  void add(int a, int b, int c) {
  	e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx ++ ;
  }
  
  void dijkstra() {
  	memset(dist, 0x3f, sizeof dist);
  	dist[s] = 0;
  	priority_queue<pii> heap;
  	heap.push({0, s});
  	while (heap.size()) {
  		auto t = heap.top();
  		heap.pop();
  
  		int no = t.y;
  		if (st[no]) continue;
  		st[no] = true;
  
  		for (int i = h[no]; ~i; i = ne[i]) {
  			int j = e[i];
  			if (dist[j] > dist[no] + w[i]) {
  				dist[j] = dist[no] + w[i];
  				if (!st[j]) heap.push({-dist[j], j});
  			}
  		}
  	}
  }
  
  int main() {
  	scanf("%d%d%d", &n, &m, &s);
  	memset(h, -1, sizeof h);
  	while (m -- ) {
  		int a, b, c;
  		scanf("%d%d%d", &a, &b, &c);
  		add(a, b, c);
  	}
  
  	dijkstra();
  
  	for (int i = 1; i <= n; i ++ )
  		printf("%d ", dist[i]);
  	return 0;
  }
  

---