图（Graph）

简介(Introduction)

图 (graph) 是一个二元组 \(G=(V(G), E(G))\)。其中 \(V(G)\) 是非空集，称为 点集 (vertex set)
对于 \(V\) 中的每个元素，我们称其为 顶点 (vertex) 或 节点 (node)，简称 点；\(E(G)\) 为 \(V(G)\) 各结点之间边的集合，称为 边集 (edge set)

描述(Description)

1. 基本概念：

   • 自环 \((loop)\)： 对 \(E\) 中的边 \(e = (u, v)\)，若 \(u = v\)，则 \(e\) 被称作一个自环。

   • 重边 \((multiple\ \ edge)\)： 若 \(E\) 中存在两个完全相同的边(方向相同) \(e_1, e_2\)，则它们被称作（一组）重边。

   • 度 \((degree)\)：

     • 无向图：与该节点相关的边的个数，记为 \(d(v)\)
     • 有向图：入度 + 出度
       • 入度：由其他节点指向该节点的边的个数
       • 出度：由该节点指向其他节点的边个个数

   • 路径 \((path)\) (又称 简单路径 \((simple\ \ path)\))： 对于一条迹 \(w\)，若其连接的点的序列中点两两不同（不包含重复点和边），则称 \(w\) 是一条路径。

   • 回路 \((circuit)\)： 对于一条迹 \(w\)，若 \(v_0 = v_k\)，则称 \(w\) 是一条回路。

   • 环/圈 \((cycle)\) (又称 简单回路/简单环 \((simple\ \ circuit)\))：对于一条回路 \(w\)，若 \(v_0 = v_k\) 是点序列中唯一重复出现的点对，则称 \(w\) 是一个环。

   • 稀疏图\((sparse\ \ graph)\)&稠密图\((dense\ \ graph)\)： 有很少条边或弧的图称为稀疏图，反之称为稠密图，相对的概念。

2. 性质：
   • 有向图：
     1. 所有顶点度数之和 \(= \ 边数 * 2\)
     2. 所有顶点的入度之和 \(=\) 所有顶点的出度之和
     3. \(n\) 个顶点的有向完全图有 \(n(n - 1)\) 条边
     4. \(n\) 个顶点的强联通图至少有 \(n\) 条边
   • 无向图：
     1. 所有点度数之和 \(= \ 边数 * 2\)
     2. \(n\) 个顶点的无向完全图有 \(\large \frac {n (n - 1)} 2\) 条边
     3. \(n\) 个顶点的强联通图至少有 \(n - 1\) 条边

3. 图的类型：
   • 有向图 \((Directed\ \ Graph)\)：

     对于一张有向图 \(G = (V, E)\)，对于 \(u, v \in V\)，若存在一条途径使得 \(v_0 = u, v_k = v\)，则称 \(u\) 可达 \(v\)。由定义，任意一个顶点可达自身，任意一条边的起点可达终点。（无向图中的连通也可以视作双向可达。）

     • 若一张有向图的节点 两两互相可达，则称这张图是 强连通的 (Strongly Connected)

     • 若一张有向图的边替换为无向边后可以得到一张连通图，则称原来这张有向图是 弱连通的 (Weakly Connected)

   • 无向图 \((Undirected\ \ Graph)\)：

     对于一张无向图 \(G = (V, E)\)，对于 \(u, v \in V\)，若存在一条途径使得 \(v_0 = u, v_k = v\)，则称 \(u\) 和 \(v\) 是 连通的 (connected) 。由定义，任意一个顶点和自身连通，任意一条边的两个端点连通。可以近似看作两条有向边

     • 若无向图 \(G = (V, E)\)，满足其中任意两个顶点均连通，则称 \(G\) 是 连通图 (connected graph)，\(G\) 的这一性质称作 连通性 (connectivity)。

     • 若 \(H\) 是 \(G\) 的一个连通子图，且不存在 \(F\) 满足 \(H\subsetneq F \subseteq G\) 且 \(F\) 为连通图，则 \(H\) 是 \(G\) 的一个 连通块/连通分量 (connected component)（极大连通子图）

   • 简单图 \((Simple\ \ Graph)\)：

     若一个图中 没有 自环和重边，它被称为简单图。具有至少两个顶点的简单无向图中一定存在度相同的结点

     • 多重图 \((Multigraph)\): 图中有 自环 或 重边

   • 完全图 \((Complete\ \ Graph)\)：

     • 若无向简单图 \(G\) 满足 任意不同两点间均有边，则称 \(G\) 为 完全图，\(n\) 阶完全图记作 \(K_n\)。

     • 有向完全图： 任意两个顶点之间都存在方向护卫相反的两条弧，有 \(n\) 个顶点的无向完全图有 $n × (n - 1) $ 条 弧

     • 无向完全图：任意两个顶点之间都存在边，有 \(n\) 个顶点的无向完全图有 \(n × (n - 1) / 2\) 条 边

   • 子图 \((Subgraph)\)：

     对一张图 \(G = (V, E)\)，若存在另一张图 \(H = (V', E')\) 满足 \(V' \subseteq V\) 且 \(E' \subseteq E\)，则称 \(H\) 是 \(G\) 的 子图 (Subgraph)，记作 \(H \subseteq G\)

     • 若 \(H \subseteq G\) 满足 \(V' = V\)，则称 \(H\) 为 \(G\) 的 生成子图/支撑子图 (Spanning Subgraph)

4. 图的存储：
   1. 邻接矩阵：适用于稠密图，可存有向图、无向图，无法存重边。空间复杂度：\(O(n^2)\)
   2. 邻接表：适用于稀疏图，可存有向图、无向图，可存重边。空间复杂度：\(O(n + m)\)

   邻接表详情

   3. 三元组表：适用于稀疏图，可存有向图，无向图，可存重边。常用于 \(Bellman-Ford\)算法、\(Kruskal\)算法。空间复杂度：\(O(m)\)
   4. 邻接多重表：适用于稀疏图，可存无向图，可存重边。空间复杂度：\(O(n + m)\)
   5. 十字链表：适用于稀疏图，可存有向图、无向图，无法存重边。空间复杂度：\(O(n + m)\)。

5. 图的遍历：
   1. 深度优先搜索
   2. 广度优先搜索

邻接表 存储的 时间复杂度：\(O(n + m)\)
邻接矩阵 存储的 时间复杂度：\(O(n^2)\)

示例(Example)

• 有向图 \(\&\) 无向图
  

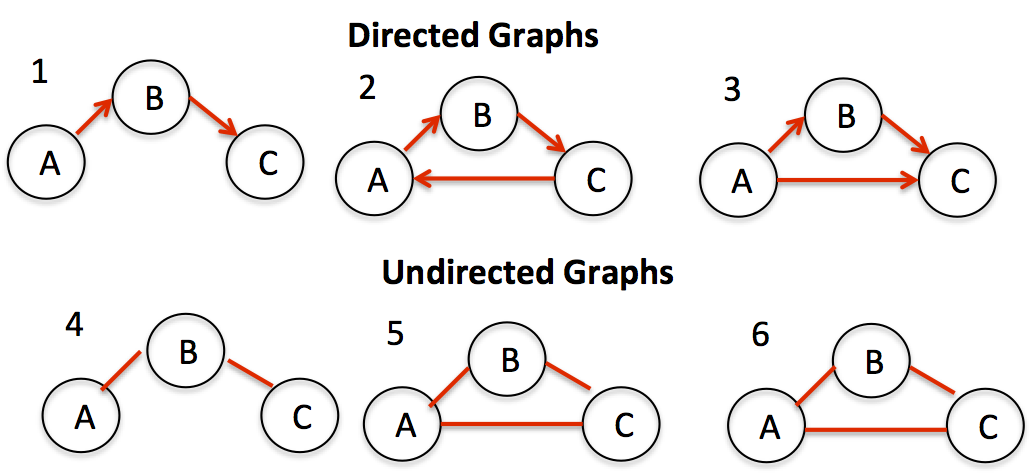
• 简单图 \(\&\) 多重图 \(\&\) 自环
  

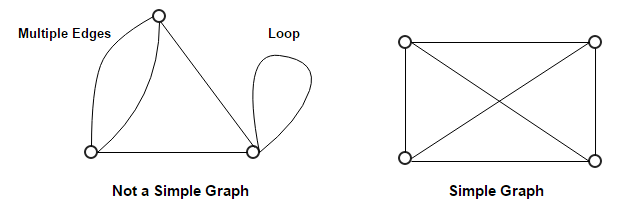
• 邻接表\((b)\) \(\&\) 邻接矩阵\((c)\)
  

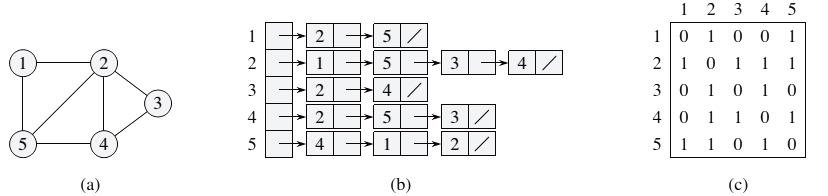
• \(DFS \ \& \ BFS\)
  

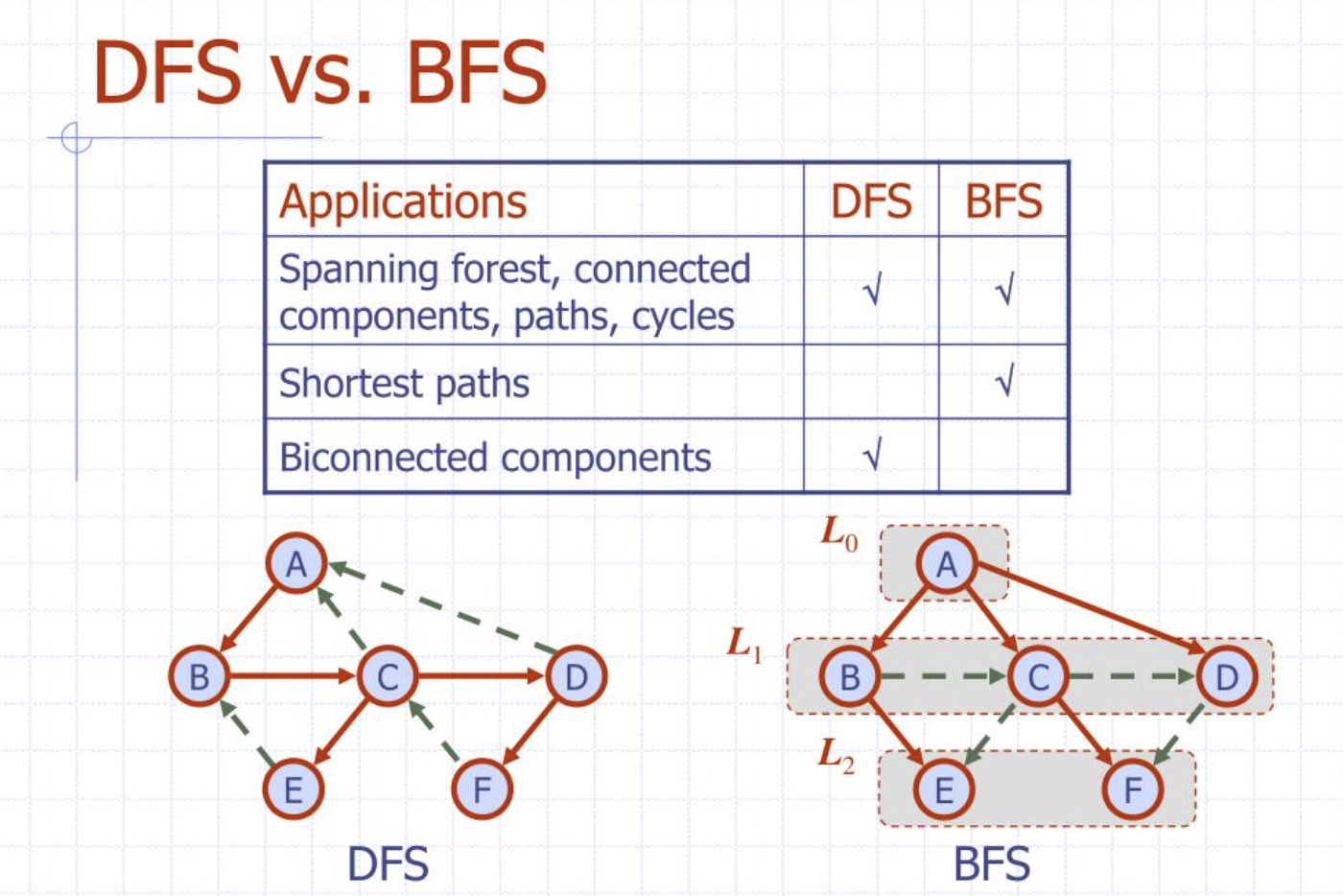
代码(Code)

• \(DFS\) :

  void dfs(int u) {
  	cout << u << " ";
  	st[u] = true;  // 标记当前点已经搜索
  	for (int i = h[u]; ~i; i = ne[i]) {
  		int j = e[i];
  		if (!st[j]) dfs(j);
  	}
  }
  

• \(BFS\)：

  void bfs(int u) {
  	memset(d,-1,sizeof d);
  	d[u] = 0;  // 层数
  	queue<int> q;
  	q.push(u);
  	while (q.size()) {
  		int t = q.front(); q.pop();
  		cout << t << ' ';
  		for (int i = h[t]; ~i; i = ne[i]) {
  			int j = e[i];
  			if (d[j] == -1) {
  				d[j] = d[t] + 1;
  				q.push(j);
  			}
  		}
  	}
  }
  

---