拓扑排序（Topological Sorting）

简介(Introduction)

对一个 有向无环图 (Directed Acyclic Graph 简称 \(DAG\) ) \(G\) 进行拓扑排序，是将 \(G\) 中所有顶点排成一个线性序列，使得图中任意一对顶点 \(u\) 和 \(v\)，若边 \(<u,v>\in E(G)\)，则 \(u\) 在线性序列中出现在 \(v\) 之前。
通常，这样的线性序列称为满足 拓扑次序 (Topological Order) 的序列，简称拓扑序列。

描述(Description)

• 如果一个序列中 存在环，那么一定 不存在拓扑序列

• 一个 有向无环图 一定存在一个拓扑序列 —— 有向无环图也称为 拓扑图

• 入度和出度

  • 入度： 通常指有向图中某点作为图中边的 终点的次数之和，即有多少条边指向这个点
  • 出度： 通常指顶点的 出边条数

  Tips： 如果一个图 不存在 入度为 \(0\) 的点，那么它一定不是 拓扑图。即 —— 存在自环
  因此可以通过把 当前位置入度为 \(0\) 的点 放入队列中，使用 \(BFS\) 搜索下一层 当前位置入度为 \(0\) 的点

• 在有向无环图中，把所有点排成一列，使得所有有向边在序列中都是从 左指向右 的操作称为 拓扑排序

• 时间复杂度：\(O(n + m)\)

示例(Example)

• 有向无环图
  

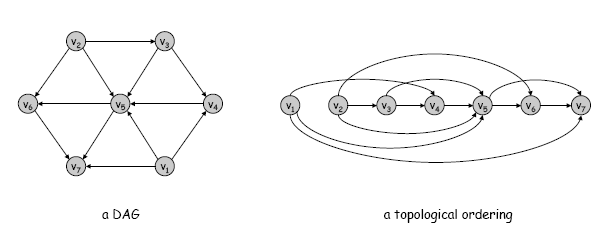
• 拓扑排序
  

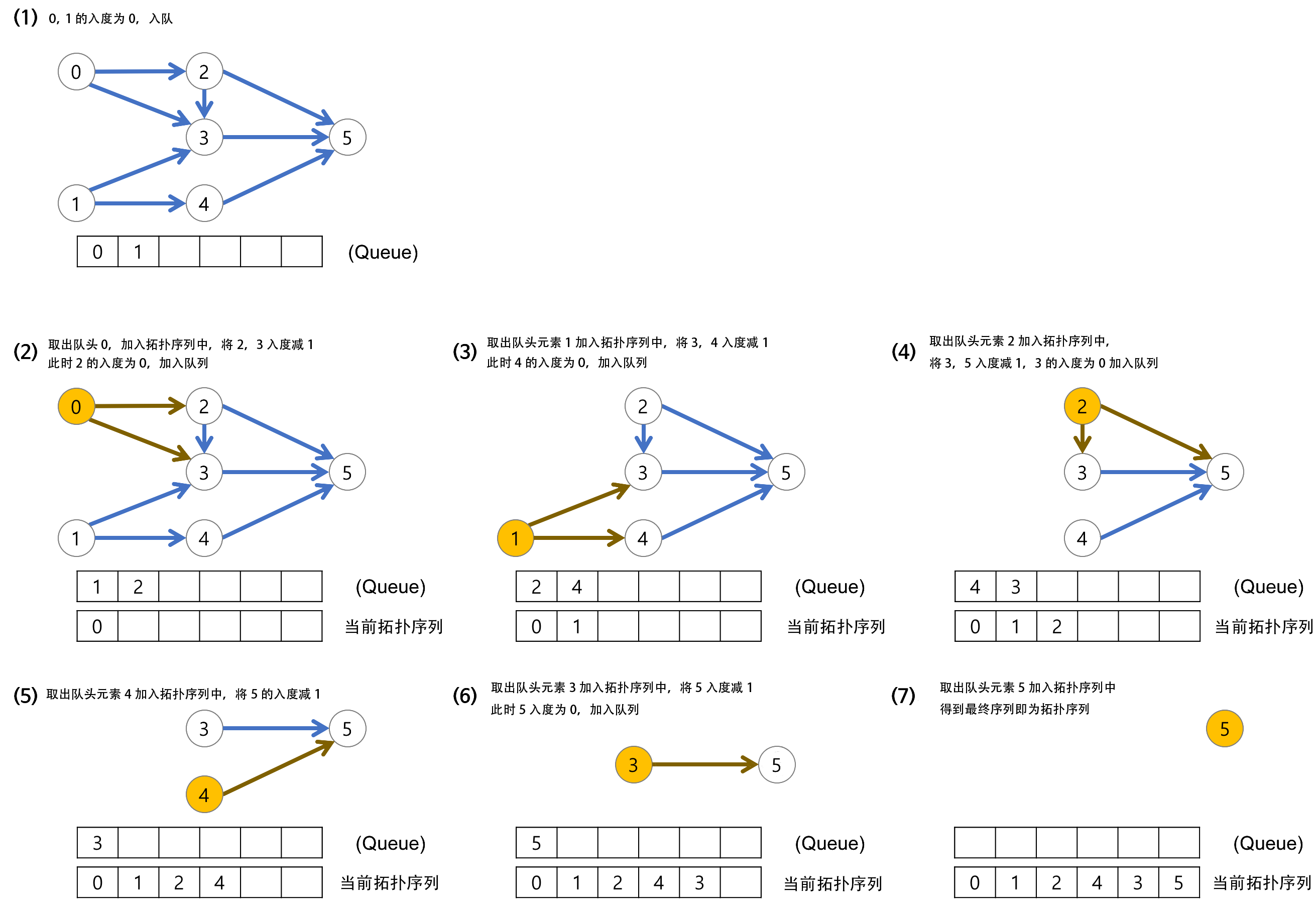
代码(Code)

// C++ Version

bool top_sort() {
    int hh = 0, tt = -1;
    //遍历每一个节点，如果入度为0则加入队列
    for (int i = 1; i <= n; i ++ ) {
        if (!d[i]) {
            q[ ++ tt ] = i;
        }
    }
    while (hh <= tt) {  // 队列不空
        int t = q[hh ++ ];  // 取出头节点
        //遍历头节点的每一个出边
        for (int i = First[t]; ~i; i = Next[i]) {
            int j = Edge[i];
            //遍历到的节点入度 减1， 如果入度为0，则加入队列
            if ( --d[j] == 0) q[ ++ tt ] = j;
        }
    }
    //判读是否全部遍历完毕，如果没有，说明存在有环
    return tt == n - 1;
}

应用(Application)

---

有向图的拓扑序列

---

给定一个 \(n\) 个点 \(m\) 条边的有向图，点的编号是 \(1\) 到 \(n\)，图中可能存在重边和自环。

请输出任意一个该有向图的拓扑序列，如果拓扑序列不存在，则输出 \(-1\)。

若一个由图中所有点构成的序列 \(A\) 满足：对于图中的每条边 \((x, y)\)，\(x\) 在 \(A\) 中都出现在 \(y\) 之前，则称 \(A\) 是该图的一个拓扑序列。

输入格式

第一行包含两个整数 \(n\) 和 \(m\)。

接下来 \(m\) 行，每行包含两个整数 \(x\) 和 \(y\)，表示存在一条从点 \(x\) 到点 \(y\) 的有向边 \((x, y)\)。

输出格式

共一行，如果存在拓扑序列，则输出任意一个合法的拓扑序列即可。

否则输出 \(-1\)。

数据范围

\(1 \le n,m \le 10^5\)

输入样例：

3 3
1 2
2 3
1 3

输出样例：

1 2 3

• 题解：

  // C++ Version
  
  #include <iostream>
  
  using namespace std;
  
  const int N = 1e5 + 10;
  
  int n, m;    //存储节点n 和 边m
  int First[N], Next[N], Edge[N], idx;
  int q[N];   //队列
  int d[N];   //入度
  
  //构建邻接表
  void add(int a, int b) {
      Edge[idx] = b, Next[idx] = First[a], First[a] = idx++;
  }
  
  //拓扑排序
  bool top_sort() {
      int hh = 0, tt = -1;
      //遍历每一个节点，如果入度为0则加入队列
      for (int i = 1; i <= n; i ++ )
          if (!d[i]) q[++tt] = i;
  
      //队列不空
      while (hh <= tt) {
          //取出头节点
          int t = q[hh ++ ];
          //遍历头节点的每一个出边
          for (int i = First[t]; i != -1; i = Next[i]) {
              int j = Edge[i];
              //遍历到的节点入度 减1， 如果入度为0，则加入队列
              if ( -- d[j] == 0) q[ ++ tt] = j;
          }
      }
      //判读是否全部遍历完毕，如果没有，说明存在有环
      return tt == n - 1;
  }
  
  int main() {
      cin >> n >> m;
      memset(First, -1, sizeof First);
      while (m -- ) {
          int a, b;
          cin >> a >> b;
          add(a, b);  // 构建邻接表
          d[b] ++;  // 入度 加1
      }
  
      // 可以完成拓扑排序
      if (top_sort()) {
          for (int i = 0; i < n; ++ i ) cout << q[i] << ' ';
          puts("");
      }
      else puts("-1");
      return 0;
  }
  

---