并查集（Disjoint Set）

  • 简介(Introduction)

每一个集合用一棵树进行表示，树根的编号就是整个集合的编号。

每个节点存储自身的父节点，使用 \(fa[x]\) 表示 \(x\) 的根节点



描述(Description)

  1. 将两个集合合并
  2. 询问两个元素是否在一个集合当中（查询祖宗节点）
  3. 方式：
    1. 路径压缩
    2. 按秩合并：（两种）
      • 深度小的树合并到深度大的树中（常见）
      • 节点数少的合并到节点数多的树中
  • 单独使用任何一种优化，可以让 单次操作 时间（均摊）复杂度：\(𝛰(\log N)\)
  • 同时使用两种优化，单次操作 时间（均摊）复杂度 可降至：\(O(α(n))\)，其中 \(𝛼\) 表示反阿克曼函数。



代码(Code)

  • 初始化：

    for (int i = 1; i <= n; i ++ ) fa[i] = i;  // 初始时，每个元素都互不相关，在自己的集合中
for (int i = 1; i <= n; i ++ ) r[i] = 1;  // 按秩合并

  • 找祖宗节点 + 路径压缩：

    int find(int x) {
	if (x == fa[x]) return x : fa[x] = find(fa[x]);
}

  • 简单合并：
    void merge(int a, int b) {  // 简单合并
	a = find(a), b = find(b);
	if (a == b) return;

	fa[a] = b;  // a 集合到 b 集合
}

  • 按秩合并：
    // C++ Version
int r[110];  // 表示树的深度

void merge(int a, int b) {
	a = find(a), b = find(b);    // 先找到两个根节点
	if (a == b) return;

	if (r[a] > r[b]) fa[b] = a;  // 判断树高度大小
	else {
		fa[a] = b;
		if (r[a] == r[b]) r[b] ++ ;   // 如果深度相同且根节点不同，则新的根节点的深度 + 1
	}
}

  • 判断是否在同一集合：

    bool judge(int a, int b) {
	if (find(a) == find(b)) return true;
	return false;
}



应用(Application)


食物链

动物王国中有三类动物 \(A,B,C\) 这三类动物的食物链构成了有趣的环形。

\(A\) 吃 \(B\)，\(B\) 吃 \(C\)，\(C\) 吃 \(A\)

现有 \(N\) 个动物，以 \(1\sim N\) 编号。

每个动物都是 \(A,B,C\) 中的一种，但是我们并不知道它到底是哪一种。

有人用两种说法对这 \(N\) 个动物所构成的食物链关系进行描述：

第一种说法是 1 X Y，表示 \(X\) 和 \(Y\) 是同类。

第二种说法是 2 X Y，表示 \(X\) 吃 \(Y\)

此人对 \(N\) 个动物，用上述两种说法，一句接一句地说出 \(K\) 句话，这 \(K\) 句话有的是真的，有的是假的。

当一句话满足下列三条之一时，这句话就是假话，否则就是真话。

  1. 当前的话与前面的某些真的话冲突，就是假话；
  2. 当前的话中 \(X\) 或 \(Y\) 比 \(N\) 大，就是假话；
  3. 当前的话表示 \(X\) 吃 \(X\)，就是假话。

你的任务是根据给定的 \(N\) 和 \(K\) 句话，输出假话的总数。

输入格式

第一行是两个整数 \(N\) 和 \(K\)，以一个空格分隔。

以下 \(K\) 行每行是三个正整数 \(D，X，Y\)，两数之间用一个空格隔开，其中 \(D\) 表示说法的种类。

若 \(D=1\)，则表示 \(X\) 和 \(Y\) 是同类。

若 \(D=2\)，则表示 \(X\) 吃 \(Y\)

输出格式

只有一个整数，表示假话的数目。

数据范围

\(1 \le N \le 50000,\)
\(0 \le K \le 100000\)

输入样例：

100 7
1 101 1
2 1 2
2 2 3
2 3 3
1 1 3
2 3 1
1 5 5

输出样例：

3

  • 思路：

    • 维护并查集的同时维护 \(d[x]\) 表示每个结点到根结点的距离，以便判断结点之间的关系。
    • 可以以距离 \(mod\ 3\) 来归为三大类：
      1. \(mod \ 3\ ······ \ 1\)，表示可以吃根结点 (代表一种动物)。
      2. \(mod \ 3\ ······ \ 2\)，可以被根节点吃。
      3. \(mod \ 3\ ······ \ 0\)，和根结点是同类。

  • 分析

    1. 当 \(x > n\) 或 \(y > n\) 即为假话
    2. 当 \(D=1\) 时，表示两个动物是同类，即在同一颗树上。 此有两种情况：
      1. 两个动物确实在一个树上，那么只要两个动物距离祖宗的差值 \((d[y]−d[x])\ mod\ 3 ==0\)，那么就一定是假话。
      2. 两个动物不在一棵树上，无法判断，认为正确，并且连通这两课树。
        设两个根节点的距离为 \(d\)，则必有关系：\(d[x]+d−d[y]\)，取 \(d[x]+d−d[y]==0\)，即：\(d=d[y]−d[x]\);
    3. 当 \(D=2\) 时，表示 \(x\) 吃 \(y\), 此有两种情况：
      1. 两个动物确实在一个树上，那么与前面类似，只要满足 \((d[x]−d[y]−1)\ mod \ 3 \ != \ 0\)，就说明这个吃的关系不成立，这是假话。
      2. 和 \(D=1\) 类似，不在同一个树上，无法判断，认为这是正确的。也有一个等量关系：\((d[x]+d−d[y])\ mod \ 3 == 1\)，取 \(d[x]+d−d[y]=1\)。有：\(d=d[y]−d[x]+1\)

  • 题解

    // C++ Version

#include <iostream>

using namespace std;

const int N = 1e5 + 10;

int n, m;
int d[N], q[N];

int find(int x) {
	if (q[x] != x) {
		int t = find(q[x]);
		d[x] += d[q[x]];
		q[x] = t;
	}
	return q[x];
}

int main() {
	scanf("%d%d", &n, &m);

	for(int i = 1; i <= n; i ++ ) q[i] = i;

	int ans = 0;
	while (m -- ) {
		int no, a, b;
		scanf("%d%d%d",&no,&a,&b);
		if (a > n || b > n) ans++;
		else {
			int x = find(a), y = find(b);
			if (no == 1) {
				if (x == y && (d[a] - d[b]) % 3) ans++;
				else if (x != y) {
					q[x] = y;
					d[x] = d[b] - d[a];
				}
			}
			else {
				if (x == y && (d[a] - d[b] - 1) % 3) ans++;
				else if (x != y) {
					q[x] = y;
					d[x] = d[b] + 1 - d[a];
				}
			}
		}
	}

	printf("%d\n",ans);

	return 0;
}

连通块中点的数量

给定一个包含 \(n\) 个点（编号为 \(1\sim n\) ）的无向图，初始时图中没有边。

现在要进行 \(m\) 个操作，操作共有三种：

  1. C a b，在点 \(a\) 和点 \(b\) 之间连一条边，\(a\) 和 \(b\) 可能相等；
  2. Q1 a b，询问点 \(a\) 和点 \(b\) 是否在同一个连通块中，\(a\) 和 \(b\) 可能相等；
  3. Q2 a，询问点 \(a\) 所在连通块中点的数量；

输入格式

第一行输入整数 \(n\) 和 \(m\)。

接下来 \(m\) 行，每行包含一个操作指令，指令为 C a b，Q1 a b 或 Q2 a 中的一种。

输出格式

对于每个询问指令 Q1 a b，如果 aa 和 bb 在同一个连通块中，则输出 Yes，否则输出 No。

对于每个询问指令 Q2 a，输出一个整数表示点 \(a\) 所在连通块中点的数量

每个结果占一行。

数据范围

\(1 \le n, m \le 10^5\)

输入样例：

5 5
C 1 2
Q1 1 2
Q2 1
C 2 5
Q2 5

输出样例：

Yes
2
3

  • 题解：

    // C++ Version

#include <iostream>

using namespace std;

const int N = 100010;

int n, m;
int q[N], size[N];

//返回x的祖宗节点
int find(int x) {
	if (q[x] == x) return x : q[x] = find(q[x]); //路经压缩
}

int main() {
	scanf("%d%d", &n, &m);
	for (int i = 1; i <= n; i ++ ) {
		q[i] = i;
		size[i] = 1;
	}

	while (m -- ) {
		char op[5];
		scanf("%s", op);
		int a, b;
		if (op[0] == 'C') {
			scanf("%d%d", &a, &b);
			if (find(a) == find(b)) continue;
			size[find(b)] += size[find(a)];
			q[find(a)] = find(b);
		}
		else if (op[1] == '1') {
			scanf("%d%d", &a, &b);
			if (find(a) == find(b)) puts("Yes");
			else puts("No");
		}
		else {
			scanf("%d", &a);
			printf("%d\n", size[find(a)]);
		}
	}
	return 0;
}

省份数量

有 \(n\) 个城市，其中一些彼此相连，另一些没有相连。如果城市 \(a\) 与城市 \(b\) 直接相连，且城市 \(b\) 与城市 \(c\) 直接相连，那么城市 \(a\) 与城市 \(c\) 间接相连。

省份 是一组直接或间接相连的城市，组内不含其他没有相连的城市。

给你一个 \(n * n\) 的矩阵 \(isConnected\) ，其中 \(isConnected[i][j] = 1\) 表示第 \(i\) 个城市和第 \(j\) 个城市直接相连，而 \(isConnected[i][j] = 0\) 表示二者不直接相连。

返回矩阵中 省份 的数量。

提示：

\(1 \le n \le 200\)

示例1：
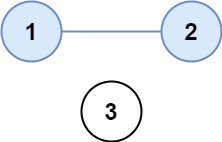
image

输入：isConnected = [[1,1,0],[1,1,0],[0,0,1]]
输出：2

示例2：

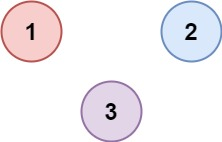
image

输入：isConnected = [[1,0,0],[0,1,0],[0,0,1]]
输出：3

  • 题解：

    // C++ Version

class Solution {
	public:
	int fa[210];

	int find(int x) {
		if (fa[x] == x) return x : fa[x] = find(fa[x]);
	}

	int findCircleNum(vector<vector<int>> &isConnected) {
		int len = isConnected.size();
		int sublen = isConnected[0].size();
		for (int i = 0; i < len; i ++ ) fa[i] = i;

		int s = len;
		for (int i = 0; i < len; i ++ )
			for (int j = 0; j < sublen; j ++ )
				if (isConnected[i][j] == 1 && i != j)
					if (find(i) != find(j)) {
						fa[find(i)] = find(j);
						s -- ;
					}
		return s;
	}
};
posted @ 2023-05-06 14:30  FFex  阅读(9)  评论(0)  编辑  收藏  举报