哈夫曼树（Huffman Tree）

简介(Introduction)

给定 \(n\) 个权值作为个叶子结点，构造一棵二叉树，若该树的带权路径长度（WPL）达到最小，称这样的二叉树为最优二叉树，也称为哈夫曼树 (Huffman Tree)。
哈夫曼树是带权路径长度最短的树，权值较大的节点离根较近。

描述(Description)

• 初始化：有 \(n\) 个权值，构造出 \(n\) 棵只有一个根节点的二叉树，记为集合 \(F = \left\{ T_1, T_2,\ ...\ ,T_n \right\}\)
• 选点：从小到大进行排序, 取出根节点权值最小的两个节点
• 合并：根据最小的两个节点，构造一棵新的二叉树，新二叉树根节点的权值是其左、右子树根结点的权值和
• 更新：从 \(F\) 中 删除 作为左、右子树的两棵二叉树，并将新建立的二叉树 加入 到集合 \(F\) 中
• 重复 \(2\)、\(3\)、\(4\) 的过程，当集合 \(F\) 中只有一个元素时，即为一棵哈夫曼树

示例(Example)

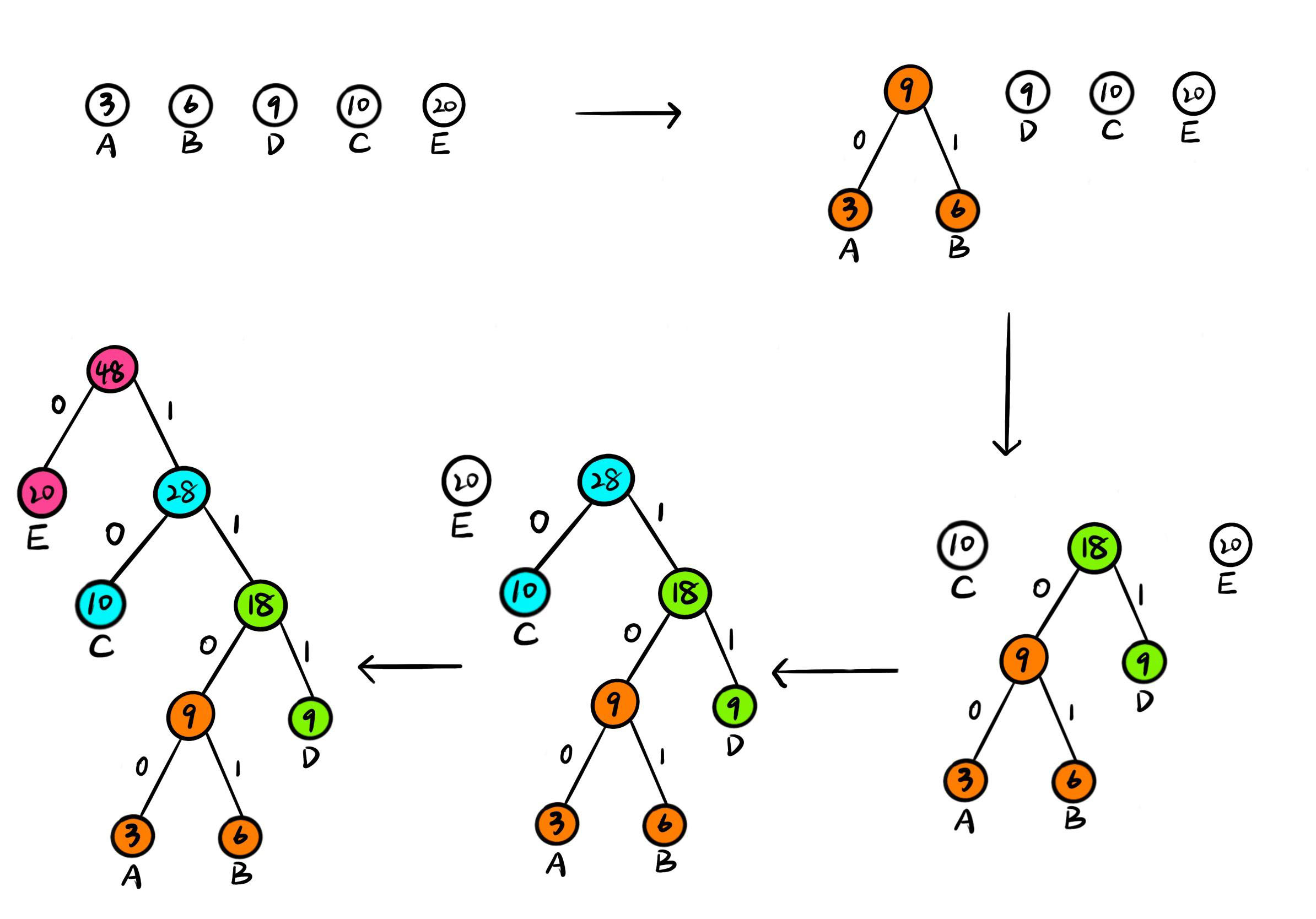
分析(Analyse)

基于示例，下面讨论哈夫曼编码

• 由于只有四个节点，我们可以将其简单的编码为：

\[\begin{array}[b] {|c|c|} \hline 字符 &\ \ \ \ \ A\ \ \ \ \ &\ \ \ \ \ B\ \ \ \ \ &\ \ \ \ \ C\ \ \ \ \ &\ \ \ \ \ D\ \ \ \ \ \ &\ \ \ \ \ E \ \ \ \ \ \\ \hline\ \ \ \ 频率\ \ \ \ &3&6 &10&9 &20 \\ \hline 编码 &000& 001&010&011&100 \\ \hline \end{array}\\ \]

• 每个字符用三位二进制数进行表示，存储总长度为：\(3\times\left( 3 + 6 + 9+ 10 + 20 \right) = 144\)
• 该方法虽简单，却无法节省空间，接下来考虑使用 变长编码：

\[\begin{array}[b] {|c|c|} \hline 字符 &\ \ \ \ \ A\ \ \ \ \ &\ \ \ \ \ B\ \ \ \ \ &\ \ \ \ \ C\ \ \ \ \ &\ \ \ \ \ D\ \ \ \ \ \ &\ \ \ \ \ E \ \ \ \ \ \\ \hline\ \ \ \ 频率\ \ \ \ &3&6 &10&9 &20 \\ \hline 编码 &1100& 1101&10&111&0 \\ \hline \end{array}\\ \]

• 存储总长度为：\(3\times4\ +\ 6 \times 4 \ + \ 10 \times 2 \ + \ 9 \times 3\ + \ 20 \times 1 = 103\)
• 压缩比为：$144\ / \ 103\approx1.398 $

Tip：哈夫曼编码中，不存在一个编码是另一个编码的 前缀(Prefix) 的情况，即两个编码不存在包含关系

• \(WPL\) 计算公式：\(WPL = \sum_{i = 1}^{n}{w_il_i}\)
• 上述示例的 \(WPL\) 值为：$WPL = 3 \times 4 \ + \ 6 \times 4 \ + \ 9 \times 3 \ + \ 10 \times 2 \ + \ 20\times 1 \ = 103 $

代码(Code)

• 已构成哈夫曼树的 \(WPL\)

  // C++ Version
  
  typedef struct TNode {
  	int val;
  	TNode *lchild, *rchild;
  } *TNode;
  
  int get_WPL(TNode root, int len) {
  	if (!root) return 0;
  	else {
  		if (!root->lchild && !root->rchild)  // 叶子节点
  			return root->weight * len;
  		else 
  			return get_WPL(root->lchild, len + 1) + get_WPL(root->rchild, len + 1);
  	}
  }
  

• 未构成哈夫曼树的 \(WPL\)

  // C++ Version
  
  int get_WPL(int arr[], int n) {
  	priority_queue<int, vector<int>, greater<int> > heap;  // 小根堆
  	for (int i = 0; i < n; i ++ ) heap.push(arr[i]);
  
  	int res = 0;
  	while (heap.size() > 1) {
  		int a = heap.top(); heap.pop();
  		int b = heap.top(); heap.pop();
  		res += a + b;
  		cout << "a = " << a << " b = " << b << " res = " << res << endl;
  		heap.push(a + b);
  	}
  	return res;
  }
  

• 计算哈夫曼编码

  typedef struct TNode {
  	int val;
  	TNode *lchild, *rchild;
  } *TNode;
  
  void get_HuffCode(TNode root, int len, int arr[]) {  
  	if (!root) return;
  
  	if (!root->lchild && !root->rchild) {
  		printf("结点为 %d 的字符的编码为: ", root->val);
  		for (int i = 0; i < len; i++) printf("%d", arr[i]);
  		puts("");
  	} 
  	else {
  		arr[len] = 0;
  		get_HuffCode(root->lchild, len + 1, arr);
  		arr[len] = 1;
  		get_HuffCode(root->rchild, len + 1, arr);
  	}
  }
  

---

应用(Application)

---

合并果子

---

在一个果园里，达达已经将所有的果子打了下来，而且按果子的不同种类分成了不同的堆。

达达决定把所有的果子合成一堆。

每一次合并，达达可以把两堆果子合并到一起，消耗的体力等于两堆果子的重量之和。

可以看出，所有的果子经过 \(n-1\) 次合并之后，就只剩下一堆了。

达达在合并果子时总共消耗的体力等于每次合并所耗体力之和。

因为还要花大力气把这些果子搬回家，所以达达在合并果子时要尽可能地节省体力。

假定每个果子重量都为 \(1\)，并且已知果子的种类数和每种果子的数目，你的任务是设计出合并的次序方案，使达达耗费的体力最少，并输出这个最小的体力耗费值。

例如有 \(3\) 种果子，数目依次为 \(1，2，9\)。

可以先将 \(1、2\) 堆合并，新堆数目为 \(3\)，耗费体力为 \(3\)。

接着，将新堆与原先的第三堆合并，又得到新的堆，数目为 \(12\)，耗费体力为 \(12\)。

所以达达总共耗费体力 \(=3+12=15\)。

可以证明 \(15\) 为最小的体力耗费值。

输入格式

输入包括两行，第一行是一个整数 \(n\)，表示果子的种类数。

第二行包含 \(n\) 个整数，用空格分隔，第 \(i\) 个整数 \(a\_i\) 是第 \(i\) 种果子的数目。

输出格式

输出包括一行，这一行只包含一个整数，也就是最小的体力耗费值。

输入数据保证这个值小于 \(2^{31}\)。

数据范围
\(1 \le n \le 10000\),
\(1 \le a_i \le 20000\)

输入样例：

3
1 2 9

输出样例：

15

• 题解

  // C++ Version
  
  #include <iostream>
  #include <algorithm>
  #include <queue>
  
  #define fio ios::sync_with_stdio(false),cout.tie(0), cin.tie(0)
  
  using namespace std;
  
  int n;
  
  int main() {
  	fio;
  	cin >> n;
  	priority_queue<int, vector<int>, greater<int> > heap;
  
  	for (int i = 0; i < n; i ++ ) {
  		int n; cin >> n;
  		heap.push(n);
  	}
  
  	int res = 0;
  	while (heap.size() > 1) {
  		int a = heap.top(); heap.pop();
  		int b = heap.top(); heap.pop();
  		res += a + b;
  		heap.push(a + b);
  	}
  
  	cout << res << endl;
  
  	return 0;
  }
  

---