树、森林

简介(Introduction)

森林由树构成，一棵树也是森林
树、森林与二叉树可以进行转化

描述(Description)

• 树的存储

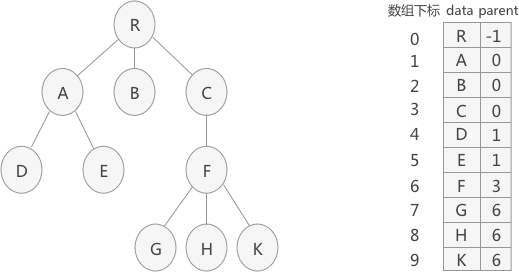
  1. 双亲表示法：取一块连续的内存空间，在存储每个结点的同时，各自都增加一个记录父结点位置的变量，在树结构中，除了树根外，每个结点都只有一个父结点
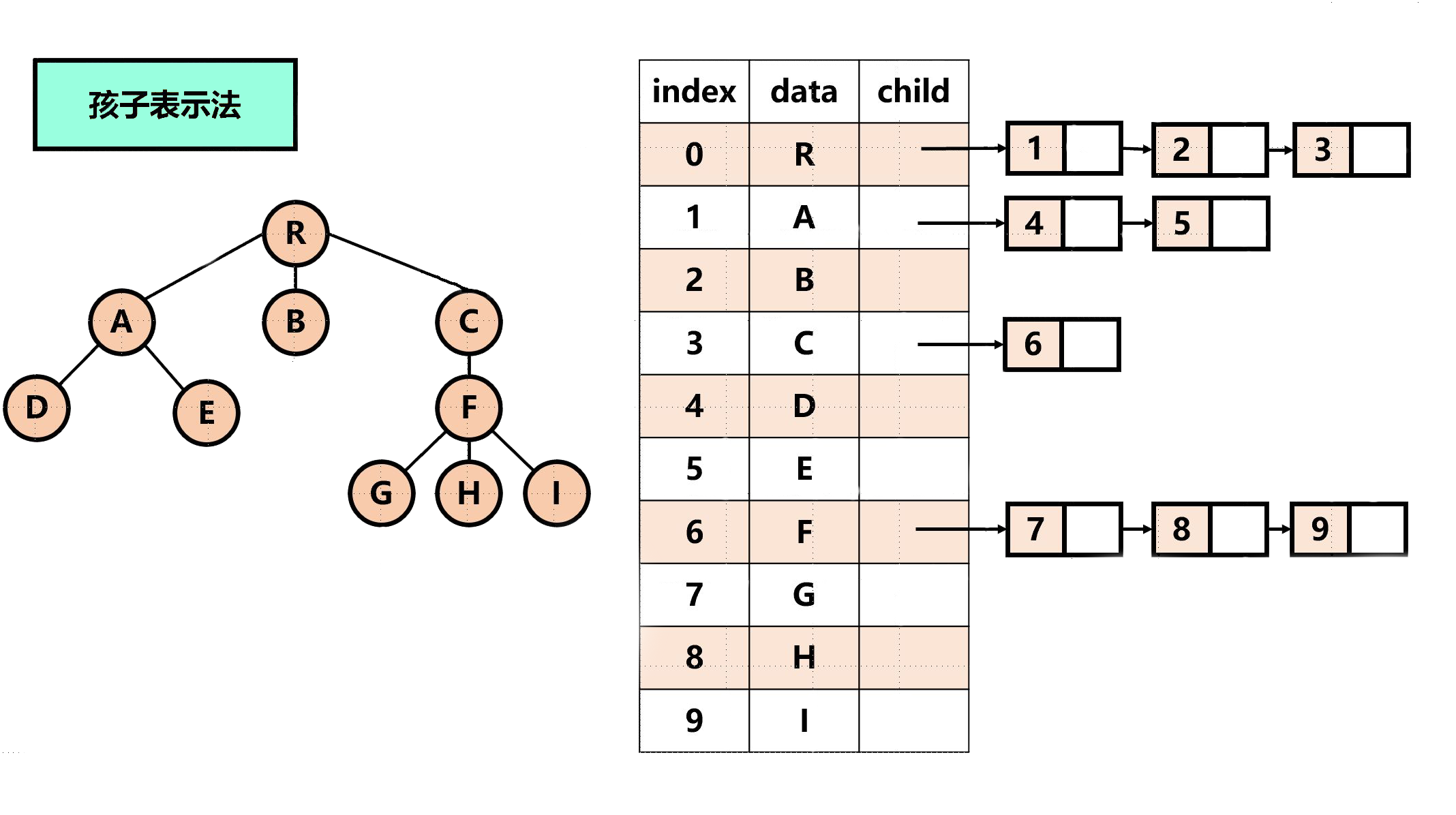
  2. 孩子表示法（邻接表存储） ：将树中的每个结点的孩子结点排列成一个线性表，用链表存储起来。对于含有 \(n\) 个结点的树来说，就会有 \(n\) 个单链表，将 \(n\) 个单链表的头指针存储在一个线性表中
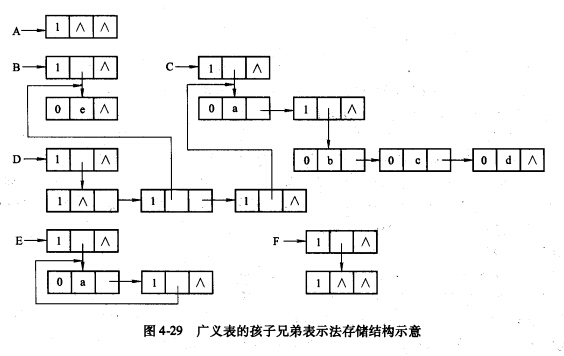
  3. 孩子兄弟表示法：相当于将树化为一颗二叉树，孩子指针域，表示指向当前结点的第一个孩子结点，兄弟结点表示指向当前结点的下一个兄弟结点 （左孩子右兄弟）
     
     

• 相互转化 —— “左孩子右兄弟”

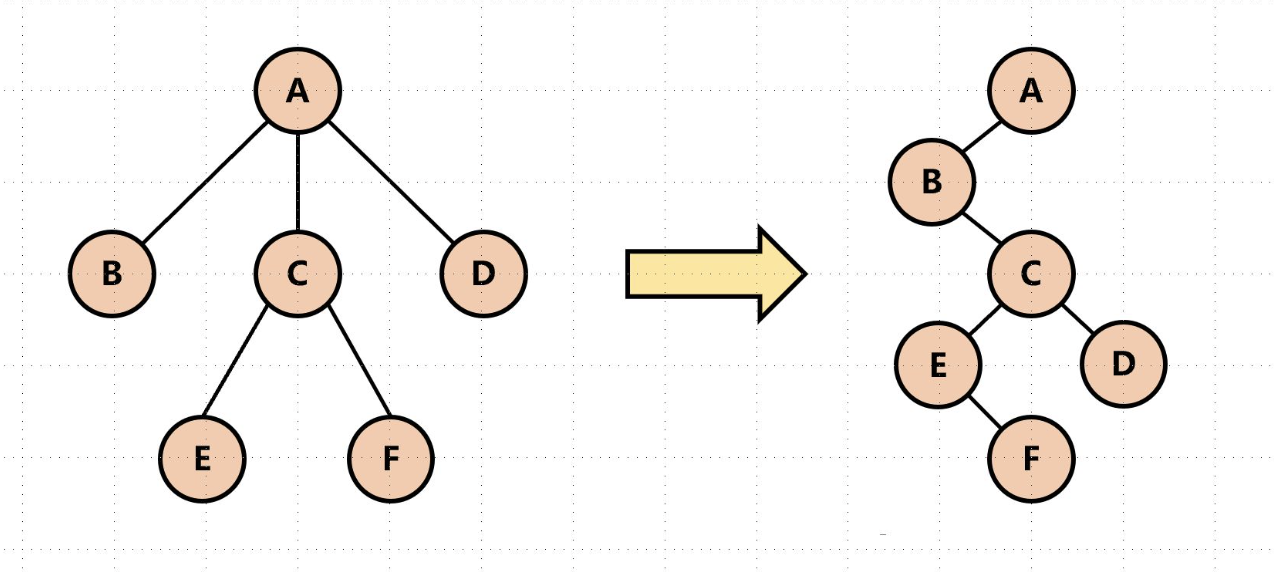
  • 树转化为二叉树：
    1. 每个结点的左指针指向它的第一个孩子结点
    2. 每个结点的右指针指向它在树中的相邻兄弟结点
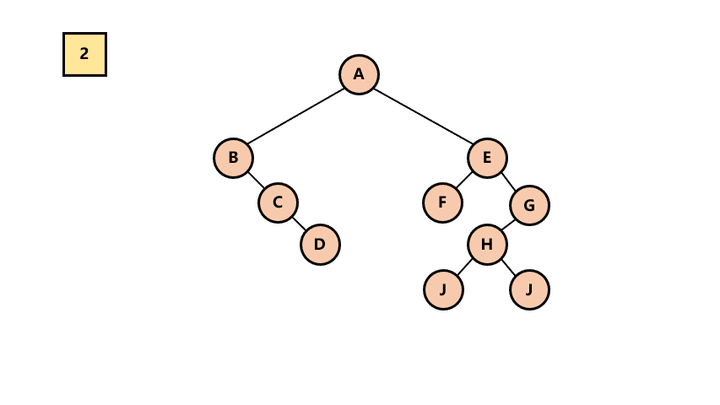
  • 森林转化为二叉树：
    1. 将第一棵树的根作为转换后的二叉树的根，将第一棵树的左子树作为转换后二叉树根的左子树
    2. 将第二棵树作为转换后二叉树的右子树
    3. 将第三棵树作为转换后二叉树根的右子树的右子树
    4. 以此类推
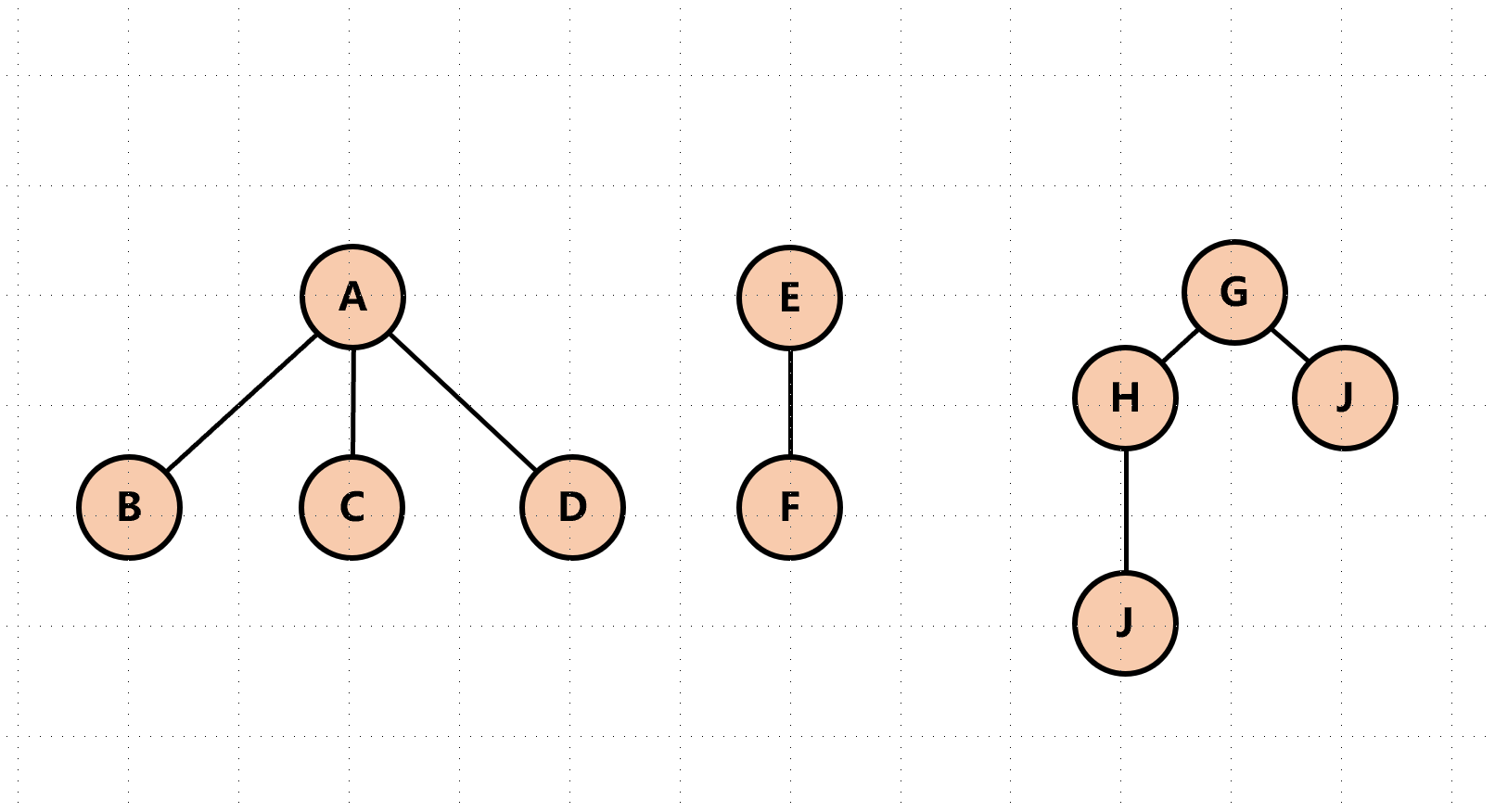
  • 二叉树转换为森林：
    1. 若二叉树非空，则二叉树的根及其左子树作为第一棵树的二叉树
    2. 二叉树根的右子树，为除第一棵树外的森林中另一棵二叉树
    3. 重复上面的操作，直到产生一个没有右子树的二叉树为止

• 树的遍历

  1. 先根遍历：若树非空，先访问根结点，再按从左到右的顺序遍历根结点的每棵子树。和相对应的二叉树的先序遍历顺序相同

  2. 后根遍历：若树非空，先按从左到右的顺序遍历根结点的每棵子树，之后在访问根结点。和相对应的二叉树的中序遍历顺序相同

  3. 层次遍历：与二叉树的层次遍历思想基本相同

• 森林的遍历

  1. 先序遍历：若森林非空，访问森林中第一棵树的根结点；先序遍历第一课树中根结点的子树森林；先序遍历除去第一棵树之后剩余的树构成的森林。

  2. 中序遍历：若森林非空，中序遍历第一课树中根结点的子树森林；访问森林中第一棵树的根结点；中序遍历除去第一棵树之后剩余的树构成的森林。

示例(Example)

• 双亲表示法
  

• 孩子表示法
  

• 孩子兄弟表示法
  

• 树转化为二叉树
  

• 森林与二叉树相互转换