队列（Queue）

简介(Introduction)

队列是一种特殊的线性表，
只允许在表的前端 \(front\) 进行删除操作，在表的后端 \(rear\) 进行插入操作
进行插入操作的端称为 队尾，进行删除操作的端称为 队头。

描述(Description)

• 队列是一种 先进先出 的结构
• 类似于人们的排队，先排队的人一定是在队列的前面，会先离开；反之，后来排队的人一定在队列后面，会后离开。

示例(Example)

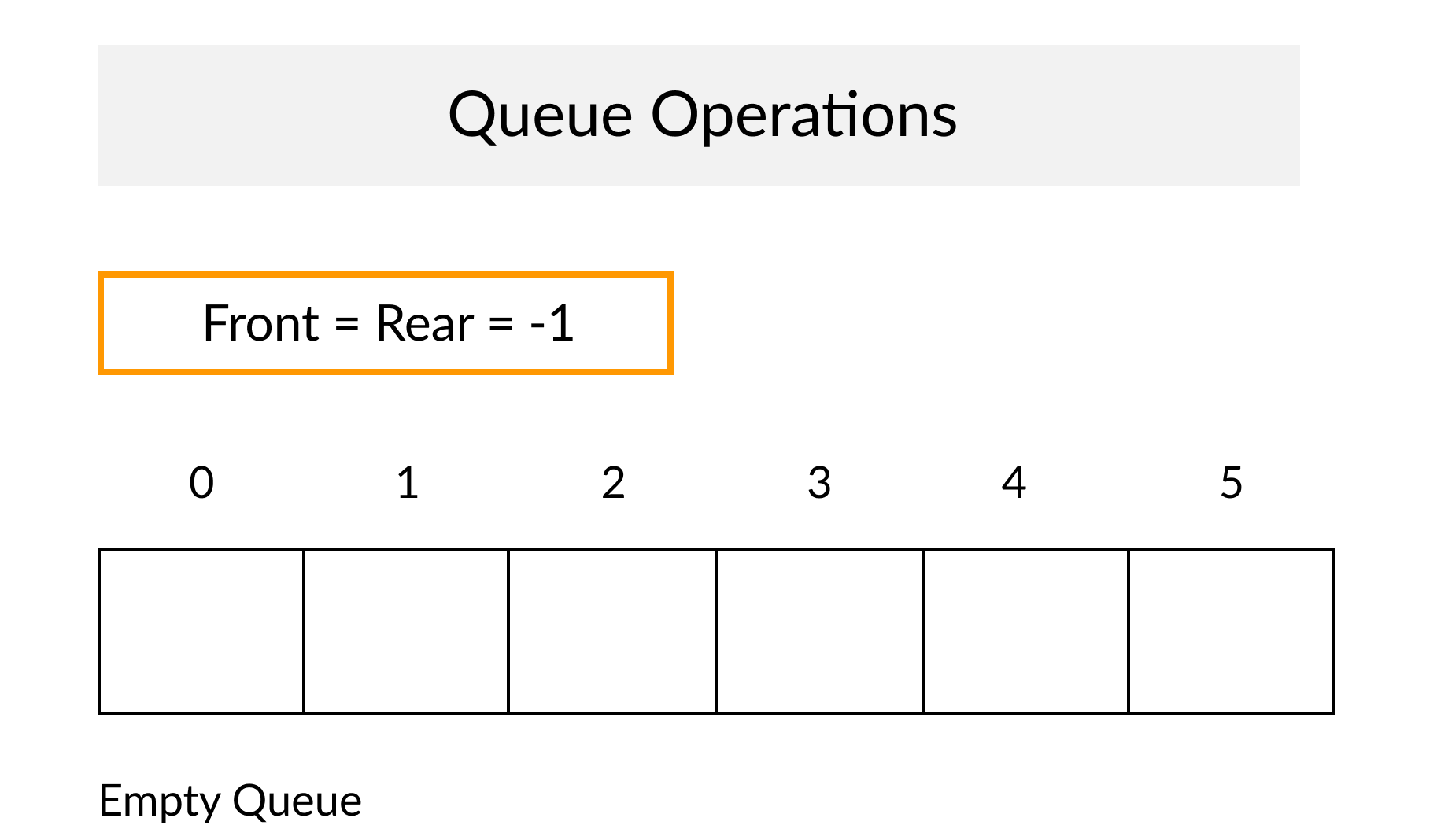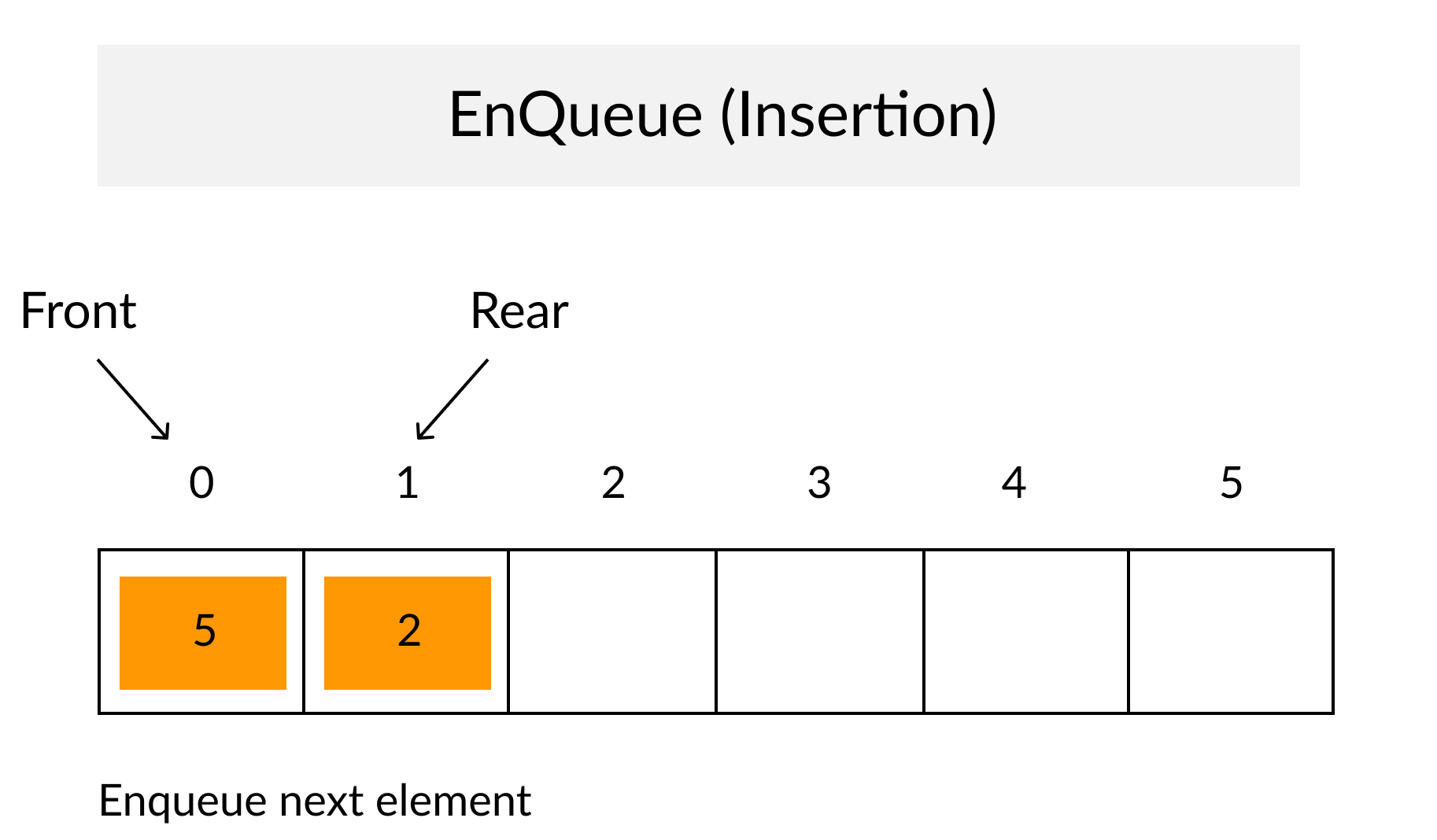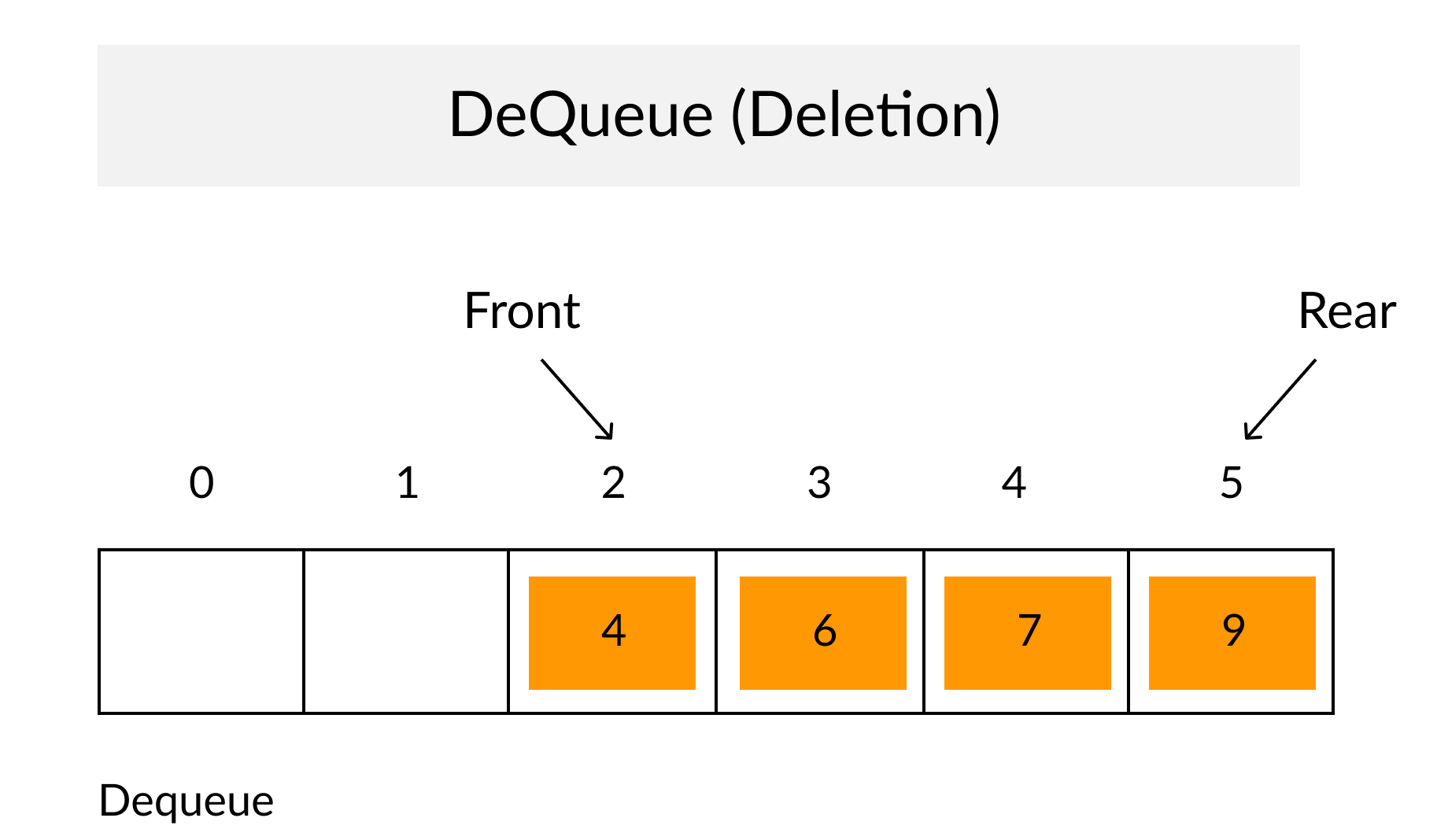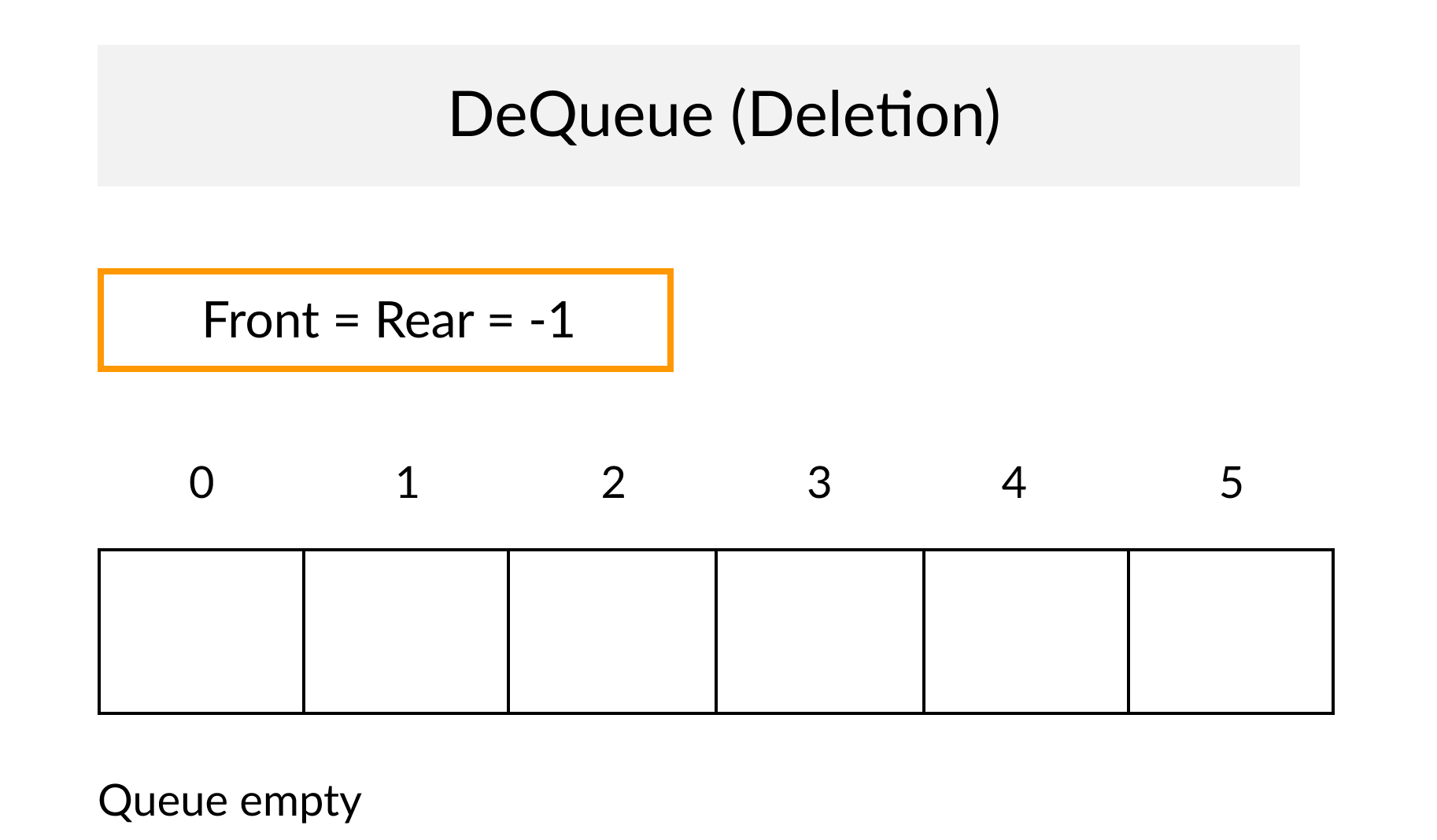
代码(Code)

• 向队尾插入一个元素

  void push(int x) {
  	q[ ++ tt ] = x;  // tt 表示队尾，初始为-1
  }
  

• 弹出一个元素

  void pop() {
  	hh ++ ;  // hh 初始为 0
  }
  

• 判断是否队空

  bool empty() {
  	if(hh <= tt) return false ;
  	return true;
  }
  

• 查询队头元素

  int query() {
  	return q[hh];
  }
  

• 单调队列写法

  int q[maxn];  // 定义队列
  int hh = 0, tt = 0;  // 相当于 int hh = 0, tt = -1;
  q[0] = 初始化时队头元素;  // 可以写成 q[ ++ tt] = 元素;
  while (hh <= tt) {
  	auto t = q[hh ++ ];  // 取出队头元素
  	q[ ++ tt] = 入队数据;  // 插入数据
  }
  

• 循环队列写法

  int q[maxn];  // 定义队列
  int hh = 0, tt = 1;  // 相当于 int hh = 0, tt = 0;
  q[0] = 初始化时队头元素;  // 可以写成 q[tt ++ ] = 元素;
  while (hh != tt) {
  	auto t = q[hh ++ ];  // 取出队头元素
  	if (hh == maxn) hh = 0;  // 循环
  
  	q[tt ++ ] = 入队数据;  // 插入数据
  	if (tt == maxn) tt = 0;  // 循环
  }
  

---

应用(Application)

---

滑动窗口

---

给定一个大小为 \(n \le 1000000\) 的数组。
有一个大小为 \(k\) 的滑动窗口，它从数组的最左边移动到最右边。
您只能在窗口中看到 \(k\) 个数字。
每次滑动窗口向右移动一个位置。
您的任务是确定滑动窗口位于每个位置时，窗口中的最大值和最小值。

输入格式

输入包含两行。
第一行包含两个整数 \(n\) 和 \(k\)，分别代表数组长度和滑动窗口的长度。
第二行有 \(n\) 个整数，代表数组的具体数值。
同行数据之间用空格隔开。

输出格式

输出包含两个。
第一行输出，从左至右，每个位置滑动窗口中的最小值。
第二行输出，从左至右，每个位置滑动窗口中的最大值。

输入样例：

8 3
1 3 -1 -3 5 3 6 7

输出样例：

-1 -3 -3 -3 3 3
3 3 5 5 6 7

• 分析：

  • 和单调栈类似，首先考虑暴力：对于每个“窗口”( 队列 )，通过遍历寻找队列中的最大值和最小值，然后输出。

  • 时间复杂度：\(0(n*k)\) 超时

  • 单调栈类似的单调性优化：

    对于队列 \([tt,hh]\) 中的所有元素寻找最小值，
    如果存在一组逆序对：$a_x \ge a_y,x < y $，那么 \(a_x\) 的存在一定是没有意义

    因此，整个队列的存在一定是单调上升的，最小值就是队头。

• 题解

  // C++ Version
  
  #include <cstdio>
  #include <iostream>
  
  using namespace std;
  
  const int N = 1e6 + 10;
  
  int n, k；
  int q[N], a[N];
  int hh, tt = -1;
  
  int main() {
  	scanf("%d%d", &n, &k);
  
  	// 查找窗口内的最小值
  	for (int i = 0; i < n; i ++ ) {
  		scanf("%d", &a[i]);
  		if (hh <= tt && q[hh] < i - k + 1) hh ++ ; // 队首不在窗口范围内，队首进行出队列，hh加1
  		// 队尾不单调 —— q[tt] 小于队尾的值，将 tt 减1，保证单调性
  		while (hh <= tt && a[q[tt]] >= a[i]) tt -- ;
  		q[ ++ tt ] = i;  // 将下标加入队列
  		if (i >= k - 1) printf("%d ", a[q[hh]]);  // 输出结果
  	}
  	puts("");
  
  	hh = 0, tt = -1;  // 重置
  	// 查找查窗口内的最大值
  	for (int i = 0; i < n; ++i) {
  		if (hh <= tt && q[hh] < i - k + 1) hh ++ ;
  		while (hh <= tt && a[q[tt]] <= a[i]) tt -- ;
  		q[ ++ tt ] = i;
  		if (i >= k - 1) printf("%d ", a[q[hh]]);
  	}
  
  	return 0;
  }
  

---